

中考专练12(几何压轴大题)(30题)-2022中考数学考点必杀500题(山东专用)(原卷版)
展开2022中考考点必杀500题
专练12(几何压轴大题)(30道)
1.(2021·青岛市崂山区第三中学九年级其他模拟)在四边形中,是边上一点,点从出发以秒的速度沿线段运动,同时点从出发,沿线段、射线运动,当运动到,两点都停止运动.设运动时间为(秒):
(1)当与的速度相同,且时,求证:
(2)当与的速度不同,且分别在上运动时(如图1),若与全等,求此时的速度和值;
(3)当运动到上,运动到射线上(如图2),若的速度为秒,是否存在恰当的边的长,使在运动过程中某一时刻刚好与全等,若存在,请求出此时的值和边的长;若不存在,请说明理由.
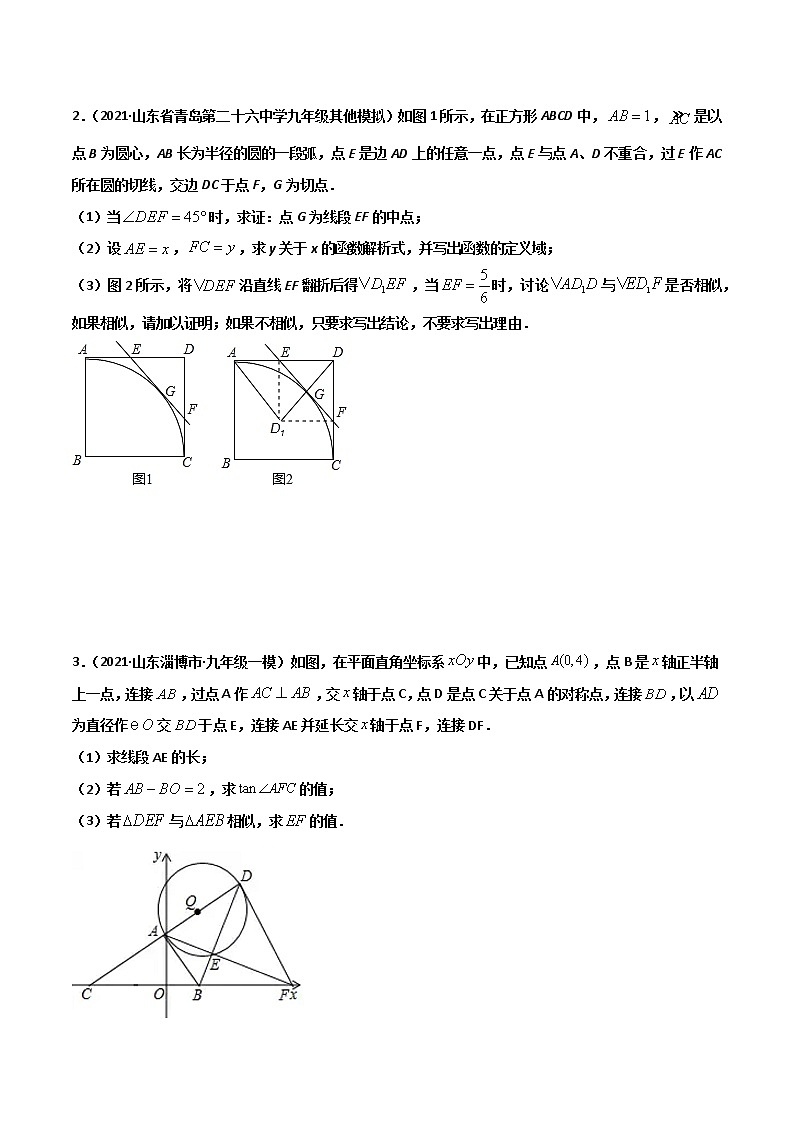
2.(2021·山东省青岛第二十六中学九年级其他模拟)如图1所示,在正方形ABCD中,,是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的任意一点,点E与点A、D不重合,过E作AC所在圆的切线,交边DC于点F,G为切点.
(1)当时,求证:点G为线段EF的中点;
(2)设,,求y关于x的函数解析式,并写出函数的定义域;
(3)图2所示,将沿直线EF翻折后得,当时,讨论与是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由.
3.(2021·山东淄博市·九年级一模)如图,在平面直角坐标系中,已知点,点B是轴正半轴上一点,连接,过点A作,交轴于点C,点D是点C关于点A的对称点,连接,以为直径作交于点E,连接AE并延长交轴于点F,连接DF.
(1)求线段AE的长;
(2)若,求的值;
(3)若与相似,求的值.
4.(2021·东营市胜利第三十九中学九年级其他模拟)如图1,已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明:四边形CEGF是正方形;
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;
(3)拓展与运用:
正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图3所示,当B,E,F三点在一条直线上时,延长CG交AD于点H,若AG=6,GH=2,求BC的长.
5.(2021·山东临沂市·九年级一模)已知:如图1所示将一块等腰三角板BMN放置与正方形ABCD的重合,连接AN、CM,E是AN的中点,连接BE.
(观察猜想)
(1)CM与BE的数量关系是________;CM与BE的位置关系是________;
(探究证明)
(2)如图2所示,把三角板BMN绕点B逆时针旋转,其他条件不变,线段CM与BE的关系是否仍然成立,并说明理由;
(拓展延伸)
(3) 若旋转角,且,求的值.
6.(2021·山东泰安市·)已知在△ABC中,AB=AC,过点B引一条射线BM,D是BM上一点.
(1)如图1,∠ABC=60,射线BM在∠ABC内,∠ADB=60,求证:∠BDC=60.
请根据以下思维框图,写出证明过程.
(2)如图2,已知∠ABC=∠ADB=30.
①当射线BM在∠ABC内,求∠BDC的度数.
②当射线BM在BC下方,请问∠BDC的度数会变吗?若不变,请说明理由;若改变,请直接写出∠BDC的度数.
(3)在第(2)题的条件下,作AF⊥BD于点F,连接CF,已知BD=6,CD=2,求△CDF的面积.
7.(2021·山东青岛市·九年级一模)如图,在矩形ABCD中,AB=6cm,BC=8cm,BD为对角线.点P为线段CD上一动点,点P从点D出发,向点C匀速运动,速度为1cm/s;点Q为BC上一动点,过点Q作BD的垂线,交BD于M,交AD于点N,点Q从点C向点B运动,速度为1cm/s,当点P停止运动时,点Q也停止运动;设运动时间为t(s)(0<t<6).
(1)当t为何值时,PQ∥BD?
(2)设四边形NQPD的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形NQPD的面积是矩形ABCD面积的?若存在,求出此时t的值;若不存在,说明理由.
8.(2021·山东青岛市·九年级一模)阅读下面材料:
小明遇到这样一个问题:如图1,在边长为a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.
小明发现,分别延长QE,MF,NG,PH交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2).
请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙不重叠),则新的正方形的边长为 ;这个新正方形的面积 (填“>”“=”或“<”)原正方形ABCD的面积;通过上述分析,可以发现正方形MNPQ的面积与△FSB的面积之间的关系是 .
(2)求正方形MNPQ的面积.
(3)如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ.若SRPQ=,求AD的长.参考小明思考问题的方法,在图3的基础上先画出图形再解决问题.
9.(2021·山东青岛市·九年级一模)如图所示,BA⊥x轴于点A,点B的坐标为(﹣1,2),将△OAB沿x轴负方向平移3个单位,平移后的图形为△EDC.
(1)直接写出点C和点E的坐标;
(2)在四边形ABCD中,点P从点A出发,沿“AB→BC→CD”移动,移动到点D停止.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t为何值时,点P的横坐标与纵坐标互为相反数;
②用含t的式子表示点P在运动过程中的坐标(写出过程);
③当5秒<t<7秒时,四边形ABCP的面积为4,求点P的坐标.
10.(2021·山东枣庄东方国际学校九年级二模)问题情境
如图1,已知矩形ABCD中,点E,F是AD,BC的中点,连接EF,将矩形ABCD沿FF剪开,得到四边形ABFE和四边形EPCD.
(1)求证:四边形EPCD是矩形;
操作探究
保持矩形EPCD位置不变,将矩形ABFE从图1的位置开始,绕点E按逆时针方向旋转.设旋转角为α(O°<α<360°)操作中,提出了如下问题,请你解答.
(2)如图2,当矩形ABFE旋转到点A落在线段EP上时,线段EF恰好经过点D,设DC与AB相交于点G.判断四边形EAGD的形状,并说明理由.
(3)在矩形ABFE旋转过程中连接线段AP和BP,当AP=BP时,求旋转角α的度数.
11.(2021·山东青岛市·九年级一模)如图,在矩形ABCD中,AB=4,AD=3,点N为BC边上的一点,且BN=n(n>0),动点P从点A出发,以每秒1个单位长的速度沿AB边向点B运动,连接NP,作射线PM⊥NP交AD于点M,设点P运动的时间是t秒(t>0).
(1)当点M与点A重合时,t等于多少秒,当点M与点D重合时,n等于多少(用含字母t的代数式表示)
(2)若n=2,则
①在点P运动过程中,点M是否可以到达线段AD的延长线上?通过计算说明理由;
②连接ND,当t为何值时,ND∥PM?
(3)过点N作NK∥AB,交AD于点K,若在点P运动过程中,点K与点M不会重合,直接写出n的取值范围.
12.(2021·胶州市初级实验中学九年级其他模拟)(问题背景)
如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=∠BAC=60°,.
(问题应用)
如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D、E、C三点共线,连接BD,
(1)求证:△ADB≌△AEC;
(2)直接写出AD、BD、CD之间的数量关系;
如图3,菱形ABCD中,∠ABC=120°,在△ABC内部作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE、CF.
(1)判断△EFC的形状,并给出证明.
(2)若AE=5,CE=2,求BF的长.
13.(2021·山东青岛市·九年级一模)已知,在Rt△ABC中,∠ACB=90°,AC=4,BC=2,D是AC边上的一个动点,将△ABD沿BD所在直线折叠,使点A落在点P处.
(1)如图1,若点D是AC中点,连接PC.
①写出BP,BD的长;
②求证:四边形BCPD是平行四边形.
(2) 如图2,若BD=AD,过点P作PH⊥BC交BC的延长线于点H,求PH的长.
14.(2021·山东省青岛实验初级中学九年级其他模拟)△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF,
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE,若已知AB=2,CD=BC,请求出GE的长.
15.(2020·济南市历城区双语实验学校九年级一模)(发现问题)
(1)如图, 已知和均为等边三角形,在上,在上, 易得线段和的数量关系是 .
(2)将图中的绕点旋转到图的位置, 直线和直线交于点
①判断线段和的数量关系,并证明你的结论.
②图中的度数是 .
(3)(探究拓展)
如图3,若和均为等腰直角三角形,,,, 直线和直线交于点, 分别写出的度数, 线段、之间的数量关系 .
16.(2020·山东东营市·九年级二模)综合与实践
在Rt△ABC中,∠ACB=90°,点D为斜边AB上的动点(不与点A,B重合).
(1)操作发现:如图①,当AC=BC=8时,把线段CD绕点C逆时针旋转90°得到线段CE,连接DE,BE.
①∠CBE的度数为 ;
②当BE= 时,四边形CDBE为正方形;
(2)探究证明:如图②,当BC=2AC时,把线段CD绕点C逆时针旋转90°后并延长为原来的两倍,记为线段CE,连接DE,BE.
①在点D的运动过程中,请判断∠CBE与∠A的大小关系,并证明;
②当CD⊥AB时,求证:四边形CDBE为矩形.
17.(2020·山东济南市·九年级其他模拟)(问题情境)(1)如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是 ;
(类比探究)
(2)如图2,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE有怎样的数量关系和位置关系,并说明理由;
(拓展提升)
(3)如图3,在(2)的条件下,连接BG,则2BG+BE的最小值为 .
18.(2020·山东青岛市·九年级一模)如图,已知菱形ABCD中,对角线AC、BD相交于点O,且AC=12cm,BD=16cm,点P从点D出发,沿DA方向匀速向点A运动,速度为2cm/s;同时,点E从点B出发,沿BO方向匀速向点O运动,速度为1cm/s,EF∥BC,交OC于点F.当点P、E中有一点停止运动时,另一点也停止运动,线段EF也停止运动,连接PE、DF(0
(2)设四边形EFDP的面积为y(),求y与t之间的函数关系式.
(3)是否存在某一时刻t,使得?若存在,求出t的值;若不存在,请说明理由.
(4)连接FP,是否存在某一时刻t,使得FP⊥AD?若存在,求出t的值;若不存在,请说明理由.
19.(2020·山东潍坊市·九年级三模)将矩形绕点顺时针旋转得到矩形,点的对应点分别为
(1)当点落在上时
①如图1,若,求证:
②如图2,交于点.若,求证:;
(2)若,
①如图3,当过点C时,则的长=_____.
②当时,作,绕点转动,当直线经过时,直线交边于,的值=______.
20.(2020·山东潍坊市·九年级一模)在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A、B的对应点分别是D、E.
(1)当点E恰好在AC上时,如图1,求∠ADE的大小;
(2)若α=60°时,点F是边AC中点,如图2,求证:四边形BEDF是平行四边形.
21.(2020·山东德州市·九年级一模)如图1,△ABC和△DEC均为等腰三角形,且∠ACB=∠DCE=90°,连接BE,AD,两条线段所在的直线交于点P.
(1)线段BE与AD有何数量关系和位置关系,请说明理由.
(2)若已知BC=12,DC=5,△DEC绕点C顺时针旋转,
①如图2,当点D恰好落在BC的延长线上时,求AP的长;
②在旋转一周的过程中,设△PAB的面积为S,求S的最值.
22.(2020·山东临沂市·九年级一模)如图,在正方形ABCD中,E是DC边上一点,(与D、C不重合),连接AE,将△ADE沿AE所在的直线折叠得到△AFE,延长EF交BC于G,连接AG,作GH⊥AG,与AE的延长线交于点H,连接CH.显然AE是∠DAF的平分线,EA是∠DEF的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于180°的角平分线),并说明理由.
23.(2020·山东德州市·九年级一模)问题探究
(1)如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B,D,E在同一直线上,连接AD,BD.
①请探究AD与BD之间的位置关系:________;
②若AC=BC=,DC=CE=,则线段AD的长为________;
拓展延伸
(2)如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90°,AC=,BC=,CD=,CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α(0°≤α<360°),作直线BD,连接AD,当点B,D,E在同一直线上时,画出图形,并求线段AD的长.
24.(2020·山东济南市·九年级二模)如图,Rt△ABC中,∠C=90°,E是AB边上一点,D是AC边上一点,且点D不与A、C重合,ED⊥AC.
(1)当sinB=时,
①求证:BE=2CD.
②当△ADE绕点A旋转到如图2的位置时(45°<∠CAD<90°).BE=2CD是否成立?若成立,请给出证明;若不成立.请说明理由.
(2)当sinB=时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2,求线段CD的长.
25.(2021·山东青岛市·九年级一模)在四边形中,点为边上一点,点为对角线上的一点,且.
(1)若四边形为正方形;
①如图1,请直接写出与的数量关系;
②将绕点逆时针旋转到图2所示的位置,连接、,猜想与的数量关系并说明理由;
(3) 如图3,若四边形为矩形,,其它条件都不变,将绕点逆时针旋转得到△,连接,,请在图3中画出草图,并求出与的数量关系.
26.(2021·山东济宁市·九年级一模)如图1,抛物线y=mx2﹣3mx+n(m≠0)与x轴交于点(﹣1,0)与y轴交于点B(0,3),在线段OA上有一动点E(不与O、A重合),过点E作x轴的垂线交直线AB于点N,交抛物线于点P.
(1)分别求出抛物线和直线AB的函数表达式;
(2)连接PA、PB,求△PAB面积的最大值,并求出此时点P的坐标.
(3)如图2,点E(2,0),将线段OE绕点O逆时针旋转的到OE′,旋转角为α(0°<α<90°),连接E′A、E′B,求E'A+E'B的最小值.
27.(2021·山东临沂市·九年级二模)(感知)(1)如图①,在四边形ABCD中,∠C=∠D=90°,点E在边CD上,∠AEB=90°,求证:=.
(探究)(2)如图②,在四边形ABCD中,∠C=∠ADC=90°,点E在边CD上,点F在边AD的延长线上,∠FEG=∠AEB=90°,且=,连接BG交CD于点H.求证:BH=GH.
(拓展)(3)如图③,点E在四边形ABCD内,∠AEB+∠DEC=180°,且=,过E作EF交AD于点F,若∠EFA=∠AEB,延长FE交BC于点G.求证:BG=CG.
28.(2021·山东济宁市·九年级一模)(1)如图1,正方形ABCD和正方形DEFG(其中ABDE),连接CE,AG交于点H,请直接写出线段AG与CE的数量关系 ,位置关系 ;
(2)如图2,矩形ABCD和矩形DEFG,AD=2DG,AB=2DE,AD=DE,将矩形DEFG绕点D逆时针旋转α(0°α360°),连接AG,CE交于点H,(1)中线段关系还成立吗?若成立,请写出理由;若不成立,请写出线段AG,CE的数量关系和位置关系,并说明理由;
(3)矩形ABCD和矩形DEFG,AD=2DG=6,AB=2DE=8,将矩形DEFG绕点D逆时针旋转α(0°α360°),直线AG,CE交于点H,当点E与点H重合时,请直接写出线段AE的长.
29.(2021·山东济南市·九年级一模)阅读以下材料,并按要求完成相应的任务.
已知平面上两点,则所有符合且的点会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆.
阿氏圆基本解法:构造三角形相似.
(问题)如图1,在平面直角坐标中,在轴,轴上分别有点,点是平面内一动点,且,设,求的最小值.
阿氏圆的关键解题步骤:
第一步:如图1,在上取点,使得;
第二步:证明;第三步:连接,此时即为所求的最小值.
下面是该题的解答过程(部分):
解:在上取点,使得,
又.
任务:
将以上解答过程补充完整.
如图2,在中,为内一动点,满足,利用中的结论,请直接写出的最小值.
30.(2021·山东济南市·九年级一模)如图1,已知和均为等腰直角三角形,点分别在线段上,且.
(1)观察猜想:如图2,将绕点逆时针旋转,连接的延长线交于点.当的延长线恰好经过点时,点与点重合,此时,
①的值为_________;
②的度数为_______度;
(2)类比探究:如图3,继续旋转,点与点不重合时,上述结论是否仍然成立,请说明理由.
(3)拓展延伸:若,当所在的直线垂直于时,请你直接写出线段的长.
初中数学中考复习 专练12(几何证明大题)(30题)2022中考数学考点必杀500题(通用版)(原卷版): 这是一份初中数学中考复习 专练12(几何证明大题)(30题)2022中考数学考点必杀500题(通用版)(原卷版),共11页。试卷主要包含了在中,,,于点,,∠AOB=∠MON=90°等内容,欢迎下载使用。
专练15-30题(几何压轴大题)2022中考数学考点必杀500题(江苏专用): 这是一份专练15-30题(几何压轴大题)2022中考数学考点必杀500题(江苏专用),文件包含专练15-30题几何压轴大题2022中考数学考点必杀500题江苏专用解析版docx、专练15-30题几何压轴大题2022中考数学考点必杀500题江苏专用原卷版docx等2份试卷配套教学资源,其中试卷共119页, 欢迎下载使用。
专练12(30题)(圆大题)2022中考数学考点必杀500题(江西专用): 这是一份专练12(30题)(圆大题)2022中考数学考点必杀500题(江西专用),文件包含专练1230题圆大题2022中考数学考点必杀500题江西专用解析版docx、专练1230题圆大题2022中考数学考点必杀500题江西专用原卷版docx等2份试卷配套教学资源,其中试卷共74页, 欢迎下载使用。












