山西省古县第一中学2020-2021学年高二上学期期中数学试题 Word版含答案

这是一份山西省古县第一中学2020-2021学年高二上学期期中数学试题 Word版含答案，共7页。试卷主要包含了已知直线经过点A，已知直线l1，当a为任意实数，直线等内容，欢迎下载使用。
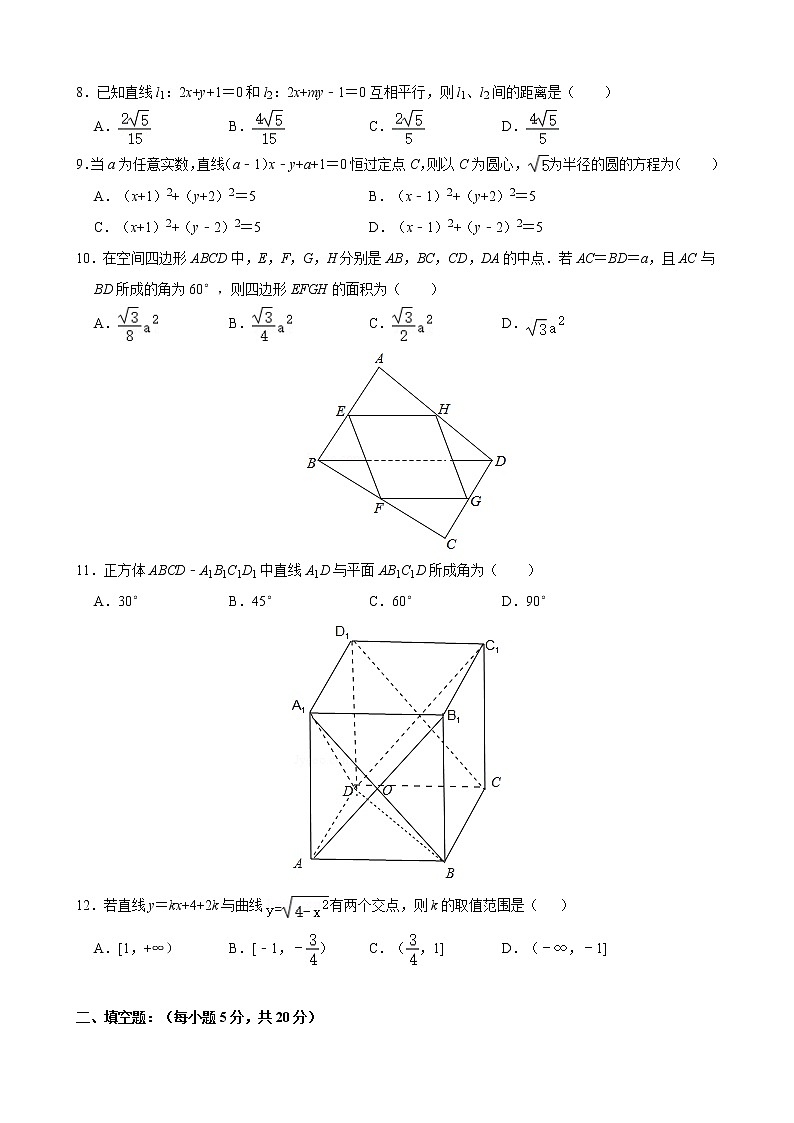
2020～2021学年第一学期期中考试试卷高二数学（时间：120分钟   满分：150分）一、选择题（每题5分，共60分）1．已知直线经过点A（0，0），B（1，﹣1），则该直线的斜率是（　）A． B．﹣1 C．1 D．﹣2．直线2x﹣3y+6＝0的斜率为k，在y轴上的截距为b，则有（　　）A．k＝，b＝2 B．k＝﹣，b＝2 C．k＝，b＝﹣2 D．k＝﹣，b＝﹣23．若直线a与平面α不垂直，那么在平面α内与直线a垂直的直线（　）A．只有一条 B．无数条 C．是平面α内的所有直线               D．不存在4．若直线l经过第二、四象限，则直线l的倾斜角的范围（　　）A．      B．[0，π）      C．         D．5．如图，三棱柱ABC﹣A1B1C1中，底面三角形A1B1C1是正三角形，E是BC的中点，则下列叙述正确的是（　　）A．CC1与B1E是异面直线 B．CC1与AE是共面直线 C．AE与B1C1是异面直线 D．AE与BB1是共面直线6.圆O:与圆C:位置关系为（       ）A．相交 B．相外切 C．内含 D．相离7.三点A（m，2）B（5，1）C（﹣4，2m）在同一条直线上，则m值为（ 　）A．2         B．         C．﹣2或        D．2或 8．已知直线l1：2x+y+1＝0和l2：2x+my﹣1＝0互相平行，则l1、l2间的距离是（　　）A． B． C． D．9．当a为任意实数，直线（a﹣1）x﹣y+a+1＝0恒过定点C，则以C为圆心，为半径的圆的方程为（　　）A．（x+1）2+（y+2）2＝5 B．（x﹣1）2+（y+2）2＝5 C．（x+1）2+（y﹣2）2＝5 D．（x﹣1）2+（y﹣2）2＝510．在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点．若AC＝BD＝a，且AC与BD所成的角为60°，则四边形EFGH的面积为（　　）A． B． C． D．11．正方体ABCD﹣A1B1C1D1中直线A1D与平面AB1C1D所成角为（　　）A．30° B．45° C．60° D．90°12．若直线y＝kx+4+2k与曲线有两个交点，则k的取值范围是（ 　）A．[1，+∞） B．[﹣1，﹣） C．（，1] D．（﹣∞，﹣1] 二、填空题：（每小题5分，共20分）13．不等式（x-1)(x-2)>0的解集为　        　．14．某几何体的三视图如图所示，则该几何体的体积为　   　．15．直线l经过直线3x+2y+6＝0和2x+5y﹣7＝0的交点，且在两坐标轴上的截距相等，则直线l的方程是                         ．16. 如果实数x，y满足等式（x﹣2）2+（y﹣1）2＝1，那么x2+y2的最小值为   　    ．三、解答题：本大题共5题，共70分．解答题应写出文字说明、演算步骤或证明过程．解答写在答题卡上的指定区域内．17．（10分）直线l经过直线x﹣2y+4＝0和直线x+y﹣2＝0的交点，且与直线x+3y+5＝0垂直，求直线l的方程．  18．（12分）如图是某几何体的三视图及尺寸，（1）求此几何体的表面积？（2）求此几何体的体积？    19.（12分）已知A（1，3），B（﹣1，0），求：（Ⅰ）A，B两点间的距离；（Ⅱ）线段AB的垂直平分线方程．   20．（12分）如图，在平行四边形ABCD中，边AD所在直线方程为2x﹣y﹣2＝0，顶点C（2，0）．（Ⅰ）求边BC所在直线的方程；（Ⅱ）求AD边上的高CE所在直线的方程．      21．（12分）已知圆心在x轴上且通过点的圆C与直线x＝﹣1相切．（Ⅰ）求圆C的方程；（Ⅱ）已知直线l经过点（0，﹣2），并且被圆C截得的弦长为，求直线l的方程     22．（12分）如图，在底面为平行四边形的四棱锥P﹣ABCD中，AB⊥AC，PA⊥平面ABCD，且PA＝AB，点E是PD的中点．（1）求证：PB∥平面AEC；（2）求二面角E﹣AC﹣B的大小．   
2020-2021学年古县一中高二（上）期中数学试卷（文理）二、选择题（每题5分，共60分） 123456789101112BABDCDDCCAAB二、填空题：（每小题5分，共20分）13.                         14.   15.　3x+4y＝0或x+y+1＝0　                 16.　6-2三、解答题：本大题共6题，共70分．解答题应写出文字说明、演算步骤或证明过程．解答写在答题卡上的指定区域内．17．（10分）解：由得，∴交点坐标为（0，2），又直线l与直线x+3y+5＝0垂直，∴直线l的斜率为3，∴直线l的方程为y＝3x+2，即3x﹣y+2＝018．（12分）解：(1)∵如图所示可知，圆锥的高为1，底面圆的直径为2，∴圆锥的母线为：2，∴根据圆锥的侧面积公式：πrl＝π××2＝2π，底面圆的面积为：πr2＝3π，∴该几何体的表面积为（3+2）π．故表面积为：（3+2）π（2）圆锥的高为1，底面圆的直径为2体积为π=19.(12分）解：（Ⅰ） ．（Ⅱ）直线AB的斜率，设线段AB的垂直平分线为l，则l的斜率． …6分线段AB的中点坐标为，即．  由直线的点斜式方程得l的方程为，即4x+6y﹣9＝0．20．(12分）解：（Ⅰ）在平行四边形ABCD中，BC∥AD由边AD所在直线方程为2x﹣y﹣2＝0，可得kBC＝kAD＝2．…3分又由顶点C的坐标为（2，0），由点斜式方程得直线BC的方程为y﹣0＝2（x﹣2），即2x﹣y﹣4＝0． （Ⅱ） 因为AD⊥CE，所以． 又由顶点C的坐标为（2，0），由点斜式方程得直线CE的方程为，即x+2y﹣2＝0．  21.（12分）解：（Ⅰ）设圆心的坐标为C（a，0），则，解得a＝1，∴C（1，0），半径r＝2，∴圆C的方程为（x﹣1）2+y2＝4．（Ⅱ）①当直线l的斜率不存在时，直线l的方程为x＝0，此时直线l被圆C截得的弦长为，满足条件；②当直线l的斜率存在时，设直线l的方程为y＝kx﹣2，由题意得，解得，∴直线l的方程为3x﹣4y﹣8＝0综上所述，直线l的方程为x＝0或3x﹣4y﹣8＝0．22.(12分）．解：（1）由PA⊥平面ABCD可得PA⊥AC又AB⊥AC，所以AC⊥平面PAB，所以AC⊥PB连BD交AC于点O，连EO，则EO是△PDB的中位线，∴EO∥PB∴PB∥平面AEC（2）取AD的中点F，连EF，FO，则EF是△PAD的中位线，∴EF∥PA又PA⊥平面ABCD，∴EF⊥平面ABCD同理FO是△ADC的中位线，∴FO∥AB，FO⊥AC由三垂线定理可知∠EOF是二面角E﹣AC﹣D的平面角．又FO＝AB＝PA＝EF∴∠EOF＝45°而二面角E﹣AC﹣B与二面角E﹣AC﹣D互补，故所求二面角E﹣AC﹣B的大小为135°．