






初中数学人教版七年级下册9.2 一元一次不等式公开课课件ppt
展开9.2 一元一次不等式 教学设计
课题 | 9.2 一元一次不等式 第1课时 | 单元 | 9 | 学科 | 初中数学 | 年级 | 七下 |
学习 目标 | 1.了解一元一次不等式的概念,掌握一元一次不等式的解法。(重点) 2.能用数轴正确表示不等式的解集.(难点) 3.能通过类比解一元一次方程的过程,获得解一元一次不等式的思路,即依据一元一次不等式的性质,将一元一次不等式化简为x>a或x<a的形式. | ||||||
重点 | 一元一次不等式的概念和解法. | ||||||
难点 | 一元一次不等式的解法和不等式的解集的表示. | ||||||
教学过程 |
教学环节 | 教师活动 | 学生活动 | 设计意图 |
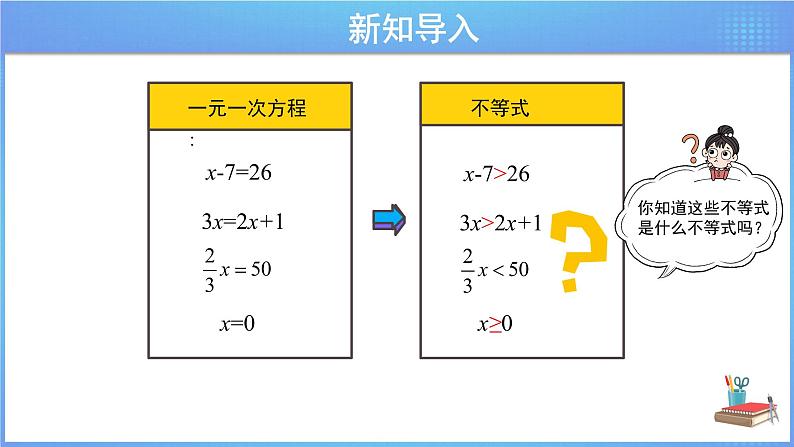
导入新课 | 【复习导入】 1.请你说说不等式的性质有哪些呢? 不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变. 即,如果a>b,那么a±c>b±c. 不等式的性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变. 即,如果a>b,c>0,那么ac>bc. 不等式的性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变. 即,如果a>b,c<0,那么ac<bc. 2.问题:观察下面的等式,哪些是一元一次方程? ①x−7=26,②x²+2x=3x+2,③3x=2x+1,④x+y=1/3, ⑤x+1/x=3,⑥ 2/3x=50,⑦x=0. 预设:①③⑥⑦ 如果这些一元一次方程①x−7=26,③3x=2x+1,⑥ 2/3x=50,⑦x=0.变成了不等式,那么这些不等式叫什么不等式呢?
|
学生思考,积极回答
|
通过复习不等式的性质,一元一次方程,为类比引出一元一次不等式打下基础。
|
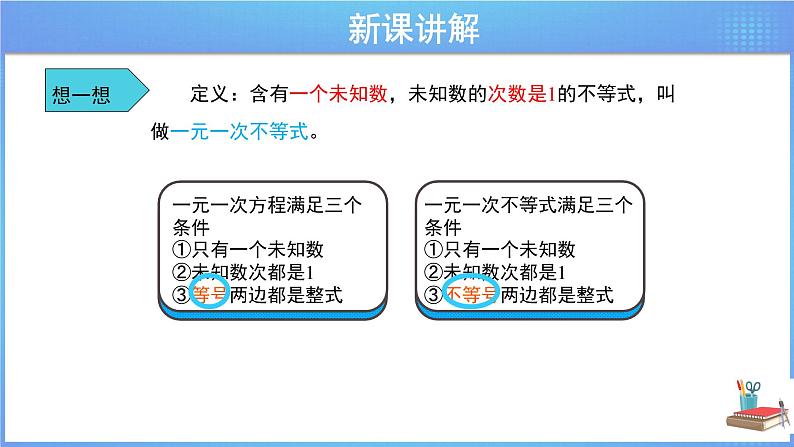
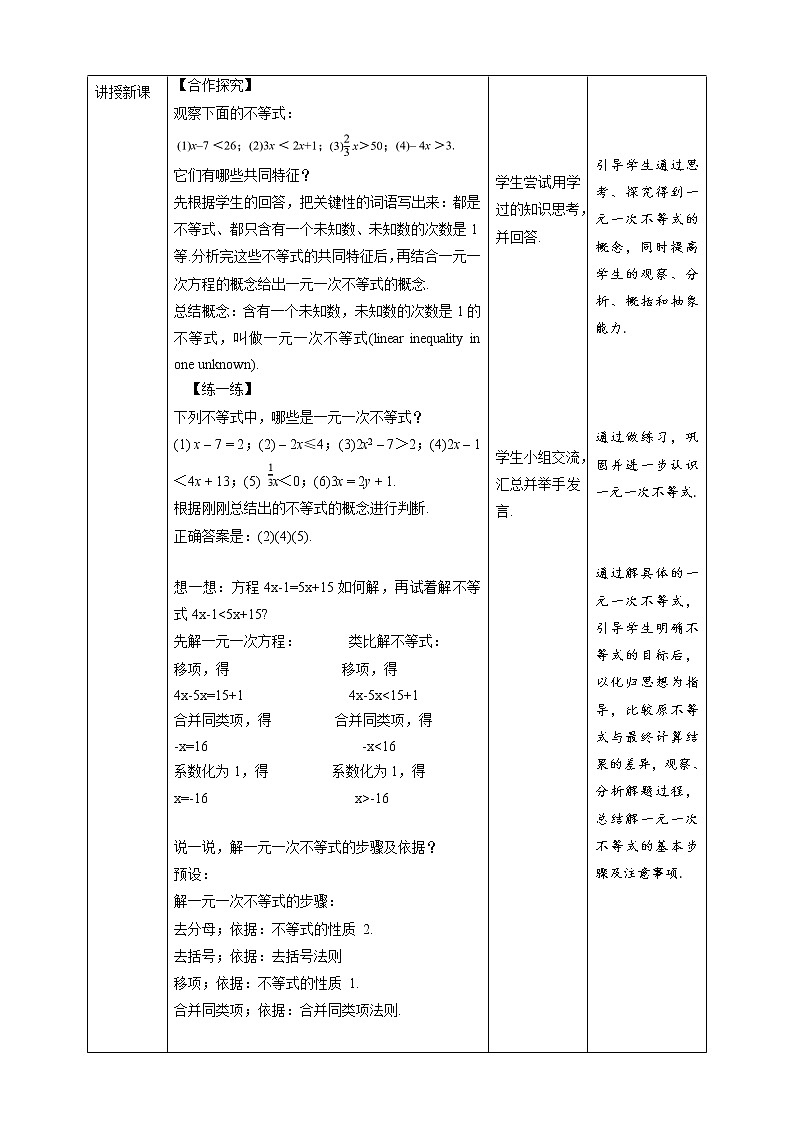
讲授新课 | 【合作探究】 观察下面的不等式: 它们有哪些共同特征? 先根据学生的回答,把关键性的词语写出来:都是不等式、都只含有一个未知数、未知数的次数是1等.分析完这些不等式的共同特征后,再结合一元一次方程的概念给出一元一次不等式的概念. 总结概念:含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式(linear inequality in one unknown). 【练一练】 下列不等式中,哪些是一元一次不等式? (1) x – 7 = 2;(2) – 2x≤4;(3)2x2 – 7>2;(4)2x – 1 <4x + 13;(5) x<0;(6)3x = 2y + 1. 根据刚刚总结出的不等式的概念进行判断. 正确答案是:(2)(4)(5).
想一想:方程4x-1=5x+15如何解,再试着解不等式4x-1<5x+15? 先解一元一次方程: 类比解不等式: 移项,得 移项,得 4x-5x=15+1 4x-5x<15+1 合并同类项,得 合并同类项,得 -x=16 -x<16 系数化为1,得 系数化为1,得 x=-16 x>-16
说一说,解一元一次不等式的步骤及依据? 预设: 解一元一次不等式的步骤: 去分母;依据:不等式的性质 2. 去括号;依据:去括号法则 移项;依据:不等式的性质 1. 合并同类项;依据:合并同类项法则.
系数化为1;依据:不等式的性质 2 或 3. |
学生尝试用学过的知识思考,并回答.
学生小组交流,汇总并举手发言.
|
引导学生通过思考、探究得到一元一次不等式的概念,同时提高学生的观察、分析、概括和抽象能力.
通过做练习,巩固并进一步认识一元一次不等式.
通过解具体的一元一次不等式,引导学生明确不等式的目标后,以化归思想为指导,比较原不等式与最终计算结果的差异,观察、分析解题过程,总结解一元一次不等式的基本步骤及注意事项.
|
| 【典型例题】 教师提出问题,学生先独立思考,解答.然后再小组交流探讨,如遇到有困难的学生适当点拨,最终教师展示答题过程. 例1解下列不等式,并在数轴上表示解集: (1) 2(1+ x)<3;(2)≥ 解:(1) 2(1+ x)<3; 去括号,得:2+2x< 3. 移项,得:2x< 3 – 2. 合并同类项,得:2x< 1. 系数化为1,得:x< 1/2. (2)去分母,得:3(2+x)≥ 2(2x–1). 去括号,得:6+3x≥4x–2. 移项,得:3x – 4x≥–2– 6. 合并同类项,得:– x ≥ –8. 系数化为1,得:x≤8. 例2 解下列不等式,并在数轴上表示解集: (1)2(x+5)<3(x-5);(2)<; (3)≥1. 解析:解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x>a或x<a的形式. 解:(1)2(x+5)<3(x-5); 去括号,得:2x+10<3x–15. 移项,得:2x – 3x<–15– 10. 合并同类项,得: – x<–25. 系数化为1,得:x>25. 这个解集在数轴上表示如下图: (2)< 去分母,得:3(x-1)<7(2x+5). 去括号,得:3x-3<14x+35. 移项,得:3x – 14x<35+3. 合并同类项,得: –11 x<38. 系数化为1,得:x>. 这个解集在数轴上表示如下图: (3)≥1. 去分母,得:2(x+1)≥3(2x–5)+12. 去括号,得:2x+2≥6x–15+12. 移项,得:2x–6x≥–15+12 – 2. 合并同类项,得: –4 x≥–5. 系数化为1,得:x≤. 这个解集在数轴上表示如下图:
【课堂练习】 教师给出练习,随时观察学生完成情况并相应指导,最后给出答案,根据学生完成情况适当分析讲解. 1. 下列不等式中,是一元一次不等式的有( ) ①3x﹣7>0;②2x+y>3;③2x2﹣x>2x2﹣1; ④ +1<7. A.1个 B.2个 C.3个 D.4个 预设:B
(1) 3-x < 2x+6; 解:移项、合并同类项,得 -x-2x < 6-3,即-3x<3, 两边同时除以-3,得 x > -1. 在数轴上表示如图: (2) 2-2x > 4; 解:移项、合并同类项,得 2x < 2-4,即 2x<-2, 两边同时除以2,得 x< -1. 在数轴上表示如图: (3) 解:两边同时除以-7,得 x≥ -7. 在数轴上表示如图: 3.当x或y满足什么条件下,下列关系成立? (1)2(x+1)大于或等于1; (2)4x与7的和不小于6; (3)y与1的差不大于2y与3的差; (4)3y与7的和的四分之一小于–2. 解析:先根据每个小题的描述列出正确的一元一次不等式,然后按照解一元一次不等式的步骤计算即可. 答案:x≥;x≥–;y≥2;y<–5.
|
学生思考、计算并回答.
自主完成练习,然后集体交流评价.
|
通过练习,进一步巩固所学知识,加深理解.培养学生在具体情境中分析问题和解决问题的能力.
通过练习,进一步巩固所学知识,加深理解.培养学生在具体情境中分析问题和解决问题的能力.
|
课堂小结 | 以思维导图的形式呈现本节主要内容:
| 回顾本节课所讲的内容 | 通过小结让学生进一步熟悉巩固本节课所学的知识. |
板书 | 1.概念: 含有一个未知数,未知数的次数是1的不等式, 叫做一元一次不等式。 2.解一元一次不等式的步骤: 去分母:不等号两边各项都乘所有分母的最小公倍数. 去括号:当括号前是“–”时,要注意括号内各项变号. 移项:从不等号的一边移到另一边,注意变号. 合并同类项:注意同类项前边的系数. 系数化为1:不等式两边乘(或除以)同一个负数时,不等号变向. 3.例题讲解 |
|
|
初中人教版9.2 一元一次不等式试讲课ppt课件: 这是一份初中人教版9.2 一元一次不等式试讲课ppt课件,共20页。PPT课件主要包含了观察与思考,一元一次不等式的概念,左边不是整式,练一练,典例精析,解不等式,解方程,解移项得,合并同类项得,-x16等内容,欢迎下载使用。
人教版七年级下册9.2 一元一次不等式一等奖ppt课件: 这是一份人教版七年级下册9.2 一元一次不等式一等奖ppt课件,文件包含92一元一次不等式第1课时pptx、RJ中学数学七年级下92一元一次不等式第一课时教学详案docx等2份课件配套教学资源,其中PPT共26页, 欢迎下载使用。
初中数学人教版七年级下册9.2 一元一次不等式获奖课件ppt: 这是一份初中数学人教版七年级下册9.2 一元一次不等式获奖课件ppt,文件包含《92一元一次不等式第2课时》同步精品课件pptx、《92一元一次不等式第2课时》同步精品教案doc等2份课件配套教学资源,其中PPT共25页, 欢迎下载使用。













