鲁教版 (五四制)八年级下册2 矩形的性质与判定教课内容ppt课件

这是一份鲁教版 (五四制)八年级下册2 矩形的性质与判定教课内容ppt课件，共25页。PPT课件主要包含了表示方法，从角上看，从对角线上看，矩形的性质，再探新知，直角三角形的一个性质，比一比知关系等内容，欢迎下载使用。

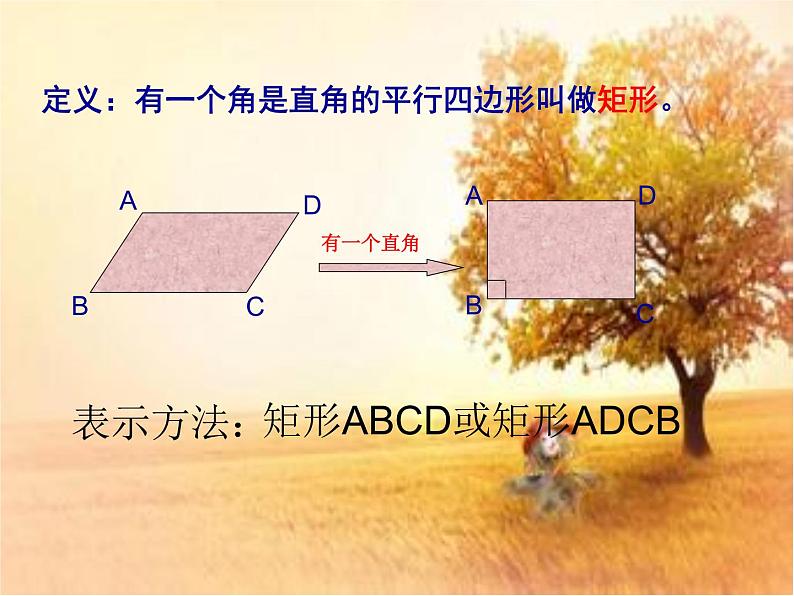
定义：有一个角是直角的平行四边形叫做矩形。
矩形ABCD或矩形ADCB
命题：矩形的四个角都是直角．
已知：如图，四边形ABCD是矩形
求证：∠A=∠B=∠C=∠D=90°
证明： ∵四边形ABCD是矩形
又 ∵ 矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D ∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°即矩形的四个角都是直角
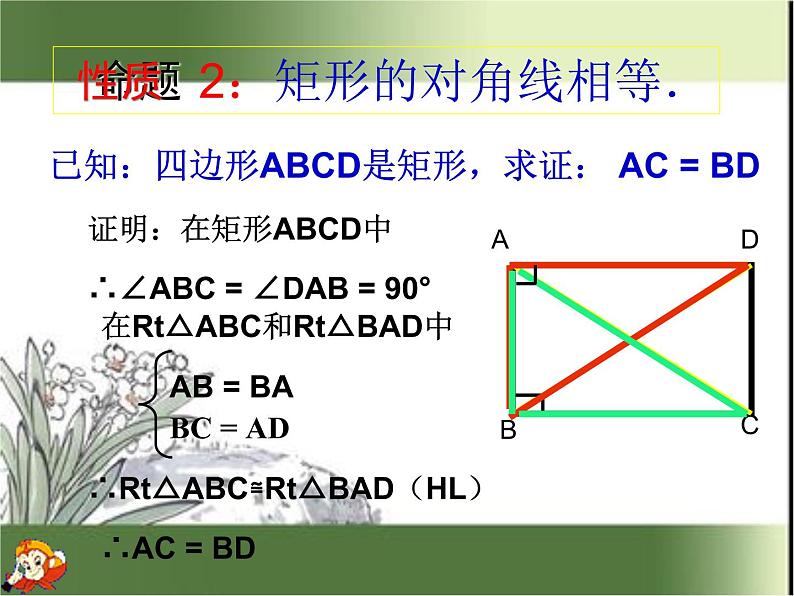
已知：四边形ABCD是矩形，求证： AC = BD
证明：在矩形ABCD中
∴∠ABC = ∠DAB = 90°
∴Rt△ABC≌Rt△BAD（HL）
　　 2：矩形的对角线相等．
AB = BA BC = AD
在Rt△ABC和Rt△BAD中
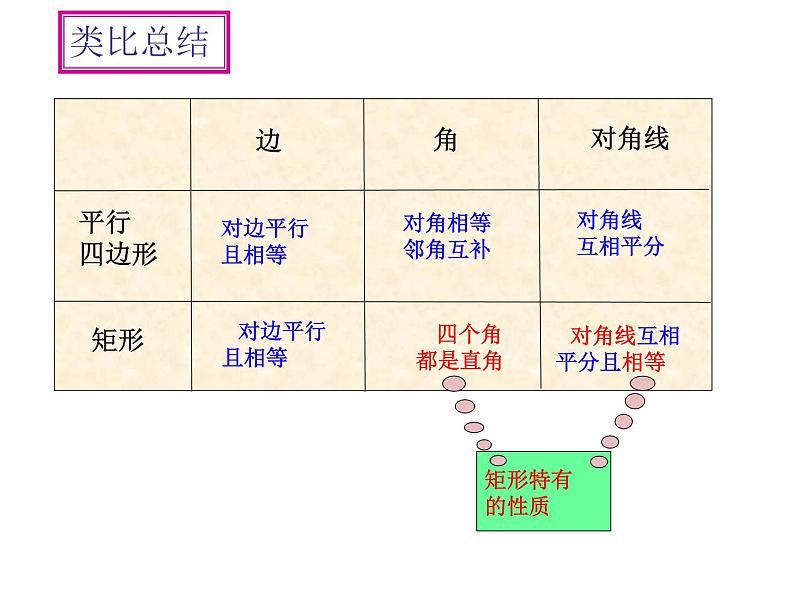
矩形的四个角都是直角．
矩形的两条对角线相等．
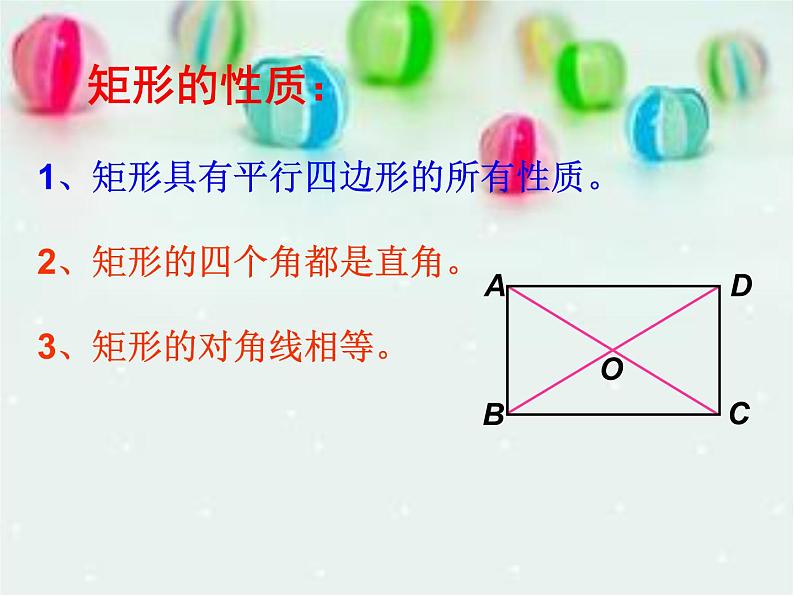
1、矩形具有平行四边形的所有性质。2、矩形的四个角都是直角。3、矩形的对角线相等。
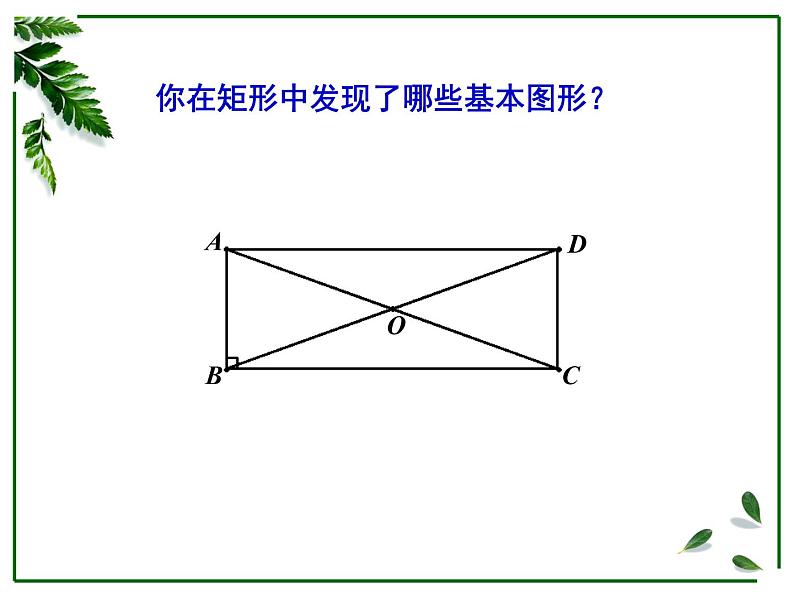
你在矩形中发现了哪些基本图形？
◆ 两对全等的等腰三角形.
◆ 四个全等的直角三角形.
◆ 两对全等的等腰三角形. ````zx``xk
公平,因为OA=OC=OB=OD
生活链接---投圈游戏
　　你还能得出哪些结论？
运用性质　解决问题 　　
　　例1　如图，矩形ABCD的两条对角线相交于点O，AB=6 ， BC=8 ．求矩形对角线AC的长．
思考：1.已知AB=6改成BC=8,或者AC=10，思路 一样吗？
　　例2　如图，矩形ABCD的两条对角线相交于点O，AB=6 , ．
小结：矩形的问题经常转化到等腰三角形或直角三角形中解决. （勾股定理、含30°的特殊直角三角形）
2.若不添条件了，还能保证0A=OB=6吗？
课本例题：如图，矩形ABCD的两条对角线相交于点O，且∠AOB=60°，AB=4 cm．求矩形对角线的长．
课本练习：一个矩形的一条对角线长为8 ，两条对角线的一个交角为120°，求这个矩形的边长
类比思考　探究性质　　
　　如图，一张矩形纸片，沿着对角线剪去一半
　　Rt△ABC中，BO是一条怎样的线段？它的长度与斜边AC有什么数量关系？
观察图中的Rt△ABC，在Rt△ABC中，BO是斜边AC上的中线，BO与AC有什么关系？
根据矩形的性质，可以得到：
直角三角形斜边上的中线等于斜边的一半.
已知：在Rt△ABC中，∠ABC=900，BO是AC上的中线.求证: BO = AC
证明: 延长BO至D,使OD=BO, 连结AD、DC.
∵AO=OC, BO=OD∴四边形ABCD是平行四边形.
　　三位学生正在做投圈游戏，他们分别站在一个直角三角形的三个顶点处，目标物放在斜边的中点处．三个人的位置对每个人公平吗？请说明理由．
在Rt△ABC中，∠ABC=90°，AC=16，BO是斜边上的中线，则BO的长为

　直角三角形性质：直角三角形斜边上的中线 等于斜边的一半．　矩形是轴对称图形，有两条对称轴，连接对边中点 的直线是它的两条对称轴．思想方法：类比、转化、分类等重要思想
1、具有平行四边形的所有性质；2、矩形的四个角都是直角；3、矩形的对角线相等且互相平分．
矩形：有一个角是直角的平行四边形叫做矩形．