数学必修 第二册6.2 平面向量的运算教课ppt课件

这是一份数学必修 第二册6.2 平面向量的运算教课ppt课件，共20页。PPT课件主要包含了力的合成，三角形法则，物理背景位移的合成，平行四边形法则，物理背景力的合成，不共线，1同向，向量三角形不等式等内容，欢迎下载使用。

李邦河院士说：“根据我上大学以后搞数学研究的经验，数学根本上是玩概念，不是玩技巧。技巧不足道也！”
但如果向量仅停留在概念的层面上，那是没有多大意义的。
我们知道数能进行运算，因为有了运算使数的威力无穷。那么向量是否也像数一样能进行运算呢？人们从向量的物理背景及数的运算中得到启发，向量也引进运算。 本节我们就来研究平面向量的运算，探索其运算性质，体会向量运算的作用。我们先学习向量的加法。
同学们，你们知道向量的加法是怎么来的吗？
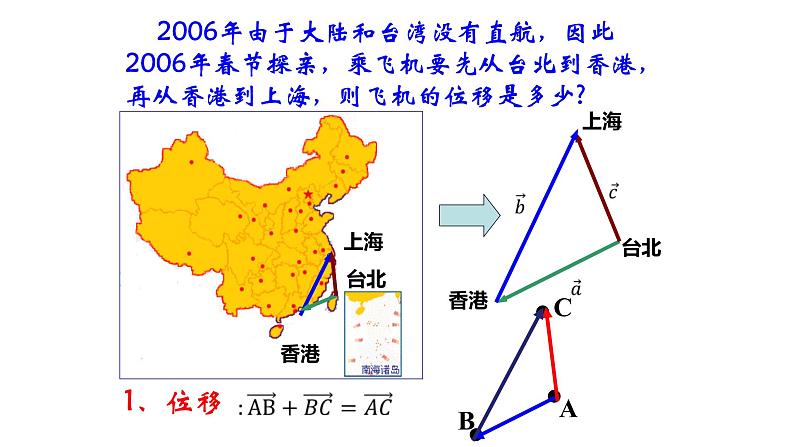
2006年由于大陆和台湾没有直航，因此2006年春节探亲，乘飞机要先从台北到香港，再从香港到上海，则飞机的位移是多少?
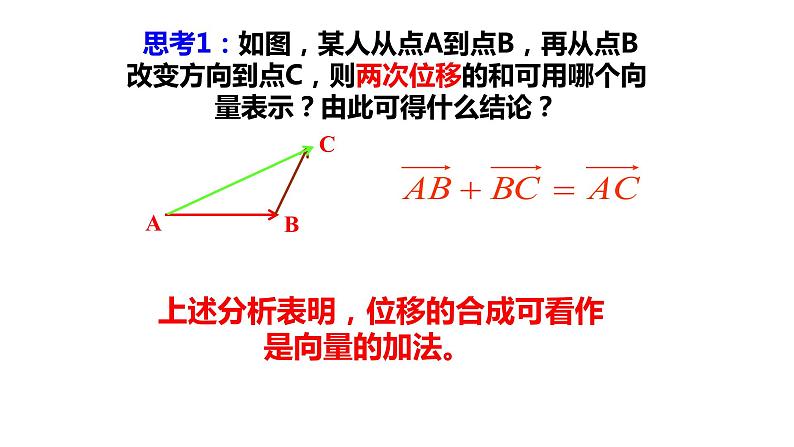
思考1：如图，某人从点A到点B，再从点B改变方向到点C，则两次位移的和可用哪个向量表示？由此可得什么结论？
上述分析表明，位移的合成可看作是向量的加法。
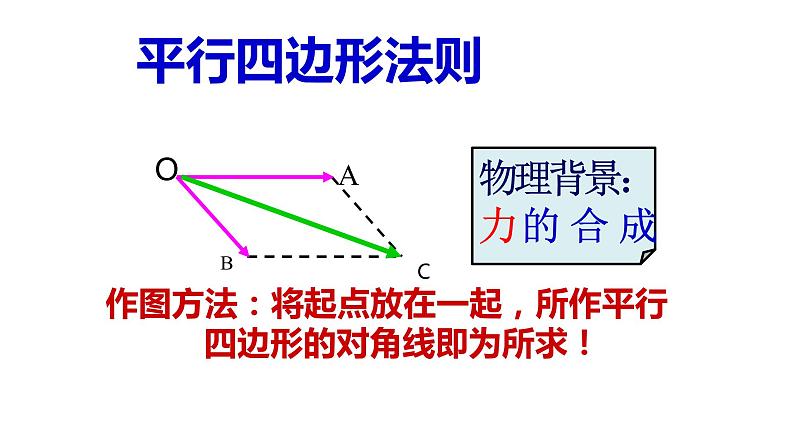
力的合成也可以看作向量的加法.
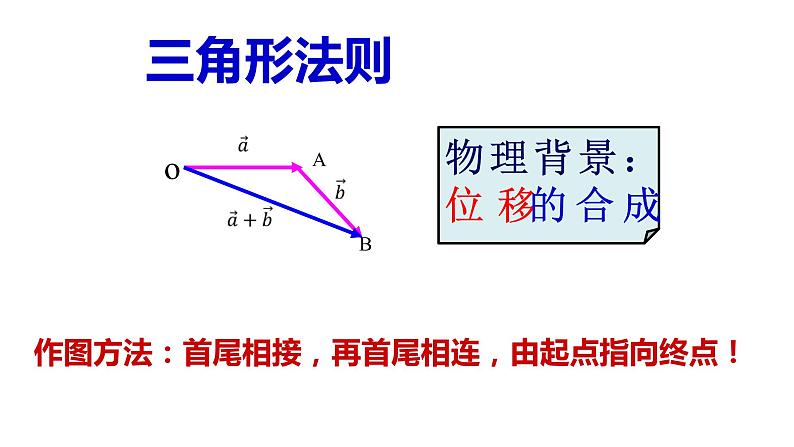
作图方法：首尾相接，再首尾相连，由起点指向终点！
作图方法：将起点放在一起，所作平行 四边形的对角线即为所求！
思考1：如图，某人从点A到点B，再从点B按原方向到点C，则两次位移的和可用哪个向量表示？由此可得什么结论？
思考2：如图，某人从点A到点B，再从点B按反方向到点C，则两次位移的和可用哪个向量表示？由此可得什么结论？
反思1：向量加法有三角形法则与平行四边形法则，数学上为什么要这样规定？我那样规定不行吗？注意什么？
答：数学上的定义、规定不是胡来的，而是有深刻的现实基础，既然有深刻的现实基础，所以数学就能解决许多现实问题。马克思主义认为理论来源于实践又对实践具有反作用或能动作用。 三角形法则是向量首尾相接再首尾相连，平行四边形法则是起点重合。
反思2 1、向量加法满足交换律与结合律的证明根据什么只能根据什么？ 答：向量加法的定义 2、数的大小可正可负，那向量的模只能是正的或等于0，请问模的符号好不好？这个符号会让你产生模是负的嫌疑吗？ 答：符号形象生动，只要与数的绝对值联系起来就可以理解。 3、在书写向量的时候记住一条，也就是符号要让人一看就知道是什么含义不要让人误会和嫌疑。举个例子零向量的书写。符号都是数学家创造出来的，是禁得起历史的考验。数学家都是天才。 4、符号表达向量的加法要知道有两层意义在运算，一层是大小的运算，一层是方向的运算。 5、实数满足交换律和结合律你觉得向量满足吗？为什么？ 答：世界是和谐的，虽然有时候无奇不有。如果不满足，世界的和谐美被破坏掉，令人不舒服。但越到高维越奇异，比如四元数。四元数（Quaternins）是由爱尔兰数学家哈密顿(William Rwan Hamiltn,1805-1865）在1843年发明的数学概念。四元数的乘法不符合交换律（cmmutative law）。大家百度：四元数 6、两向量相加如果不共线则用三角形法则或平行四边形法则，但有种情况要区别对待那就是共线，而共线又分成同向和反向但也是首位相连也符合三角形法则。
数的加法满足交换律与结合律,即对任意a,b∈R,有a+b=b+a,(a+b)+c=a+(b+c) 任意向量a,b的加法是否也满足交换律与结合律?
例2 长江两岸之间没有大桥的地方,常常通过轮渡进行运输.如图所示,一艘船从长江南岸A点出发,以5km/h的速度向垂直于对岸的方向行驶,同时江水的速度为向东2km/h.(1)试用向量表示江水速度、船速以及船实际航行的速度(保留两个有效数字)(2)求船实际航行的速度的大小与方向(用与江水速度间的夹角表示,精确到度).
(1)试用向量表示江水速度、船速以及船实际航行的速度(保留两个有效数字)