


高中数学人教A版 (2019)必修 第二册8.5 空间直线、平面的平行课文内容ppt课件
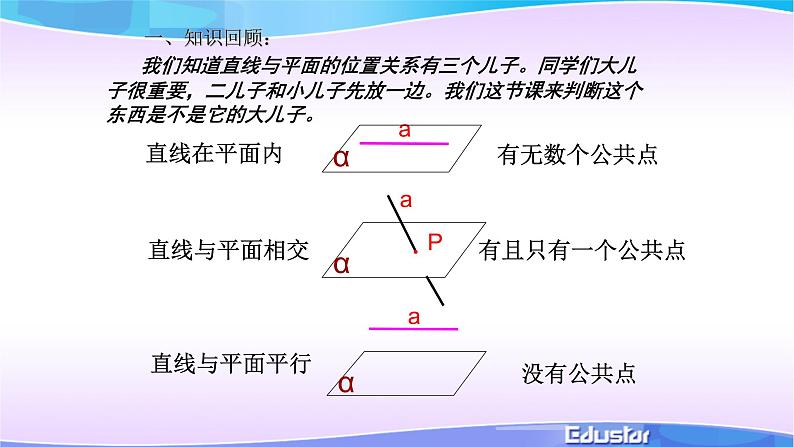
展开我们知道直线与平面的位置关系有三个儿子。同学们大儿子很重要,二儿子和小儿子先放一边。我们这节课来判断这个东西是不是它的大儿子。
怎样判定直线与平面平行呢?
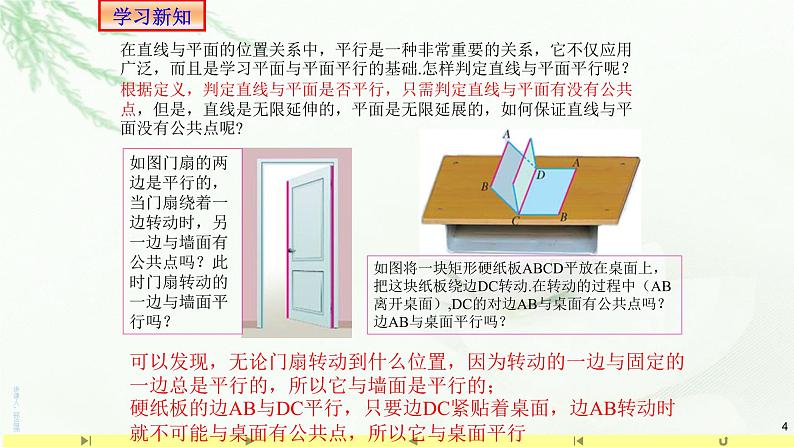
在直线与平面的位置关系中,平行是一种非常重要的关系,它不仅应用广泛,而且是学习平面与平面平行的基础.怎样判定直线与平面平行呢?根据定义,判定直线与平面是否平行,只需判定直线与平面有没有公共点,但是,直线是无限延伸的,平面是无限延展的,如何保证直线与平面没有公共点呢?
如图门扇的两边是平行的,当门扇绕着一边转动时,另一边与墙面有公共点吗?此时门扇转动的一边与墙面平行吗?
如图将一块矩形硬纸板ABCD平放在桌面上,把这块纸板绕边DC转动.在转动的过程中(AB离开桌面),DC的对边AB与桌面有公共点吗?边AB与桌面平行吗?
可以发现,无论门扇转动到什么位置,因为转动的一边与固定的一边总是平行的,所以它与墙面是平行的;硬纸板的边AB与DC平行,只要边DC紧贴着桌面,边AB转动时就不可能与桌面有公共点,所以它与桌面平行
直线和平面平行的判定定理:
如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
注意:使用定理时,必须具备三个条件:
(1)直线a在平面α外,(2)直线b在平面α内,(3)两条直线a、b平行
三个条件缺一不可,缺少其中任何一条,则结论就不一定成立了。
1、同学们,虽然这个定理是从生活生产实践中总结出来也是非常显然非常明显的,是我们发现的,但它不是公理而是定理,因为我们可以把它证明出来。 同学们有没有发现西方人没事找事做,吃饱了撑着?正因为西方人的这种刨根究底的精神造就了西方发达的科学。在中国这些是经验,没有证明的迹象。
2、同学们,我们判断线面平行的思路是把空间问题转化为平面问题即线面平行转化为线线平行。
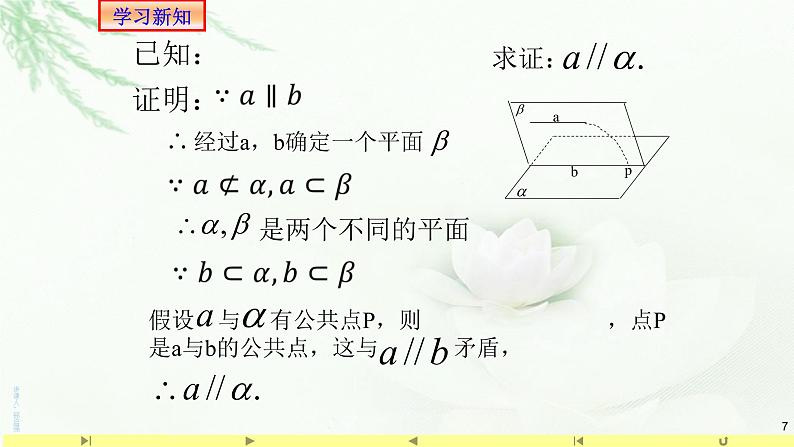
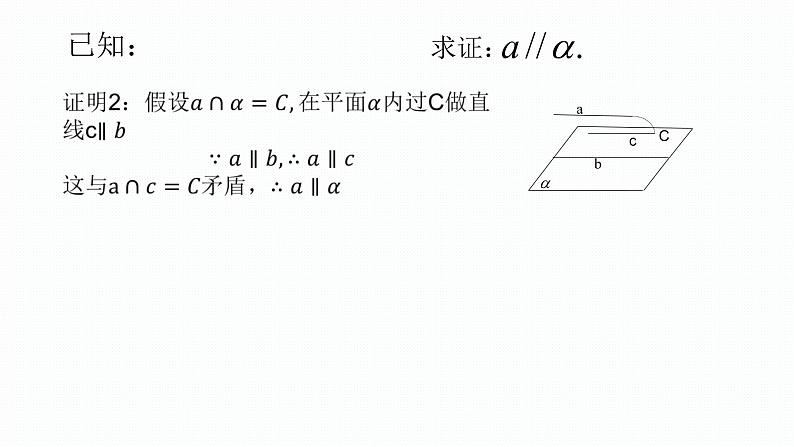
经过a,b确定一个平面
假设 与 有公共点P,则 ,点P是a与b的公共点,这与 矛盾,
1、学习数学有什么用?
荷兰数学家弗赖登塔尔的,他说:“与其说是学习数学,还不如说是学习‘数学化’;与其说是学习公理系统,还不如说是学习‘公理化’;与其说是学习形式体系,还不如说是学习‘形式化’。”
数学教育家米山国藏指出:“学生进入社会后,几乎没有机会应用它们在初中或高中所学到的数学知识,因而这种作为知识的数学,通常在学生出校门后不到一两年就忘掉了,然而不管从事什么业务工作,那种铭刻于头脑中的数学精神和数学思想方法,却长期地在他们的生活和工作中发挥着重要作用。”
所以学习数学,数学忘记了,但数学化不会忘记,学习公理,公理忘记了,但公理化不会忘记,学习形式体系,形式体系忘记了,但形式化不会忘记。也就是数学化、公理化、形式化一辈子都对你产生影响。
中国人的思维缺陷
1、不证而论 比如不懂逻辑学上的“充足理由律”,给出论点来往往不证而论,只有论点,没有论据。
2、以“经典、经验、想当然”作为论据
参考文章:《中国人思维的五大缺陷》作者:芦笛
总结:中国数学是经验型的,结构松散毫无逻辑,中国人做事也不讲逻辑。
擅长逻辑,比如平面几何的公理系统,从几个公理出发当成起点推出定理、性质、推论。或由以定理、性质、推论为依据推出定理、性质、推论,每一步都有论据,这论据要么是公理要么是定理、性质、推论。最后形成严密的公理化系统,注意是严密,或严密的逻辑系统。逻辑学就是发达于西方. 学习数学有点就是学习西方人如何思维,高考大部分考西方的思维方式。只有算法是考中国人思维方式
同学们,书上只介绍了三个基本事实即公理,为什么? 那是因为要建立立体几何公理系统,有这三个公理就足够了,其它都可以把它推导出来,可以当推论或当性质等。其实加上公理4就真的够了,其他任何事实都可以由着四个公理加平面几何的公理和定理推导出来。。
有的同学马上想知道这三个事实即三个公理还有推导到底用在哪里?
公理系统是什么?我们前面提过。 什么是公理?那就是不证自明非常显然的事实,公理是我们证明的原点或起点,从原点或起点出发到达我们要到的地方。证明先从公理开始。证明的起点是显而易见的事实,这事实就是公理。公理是去证别人而自己是不能证明的。 同学们很多立体几何定理结论实在是太明显太显然了,比公理还显然,但注意它不是公理而是可以证明出来的性质或定理,我们中国人觉得拿过来用就可以了,但西方不然,要证明出它。这在平时的证明中可以当定理使用。注意我们证明题目时的论据都是来自于教材,教材之外的不会考到,虽然教材之外补充了许多定理、性质。 同学们有没有发现西方人没事找事做,吃饱了撑着?正因为西方人的这种刨根究底的精神造就了西方发达的科学。在中国这些是经验,没有证明的迹象。 虽然结论很显然但证明却是不容易。 定理:两条平行线一条垂直一个平面另一条也垂直这个平面 这样的定理很多。 同学们注意,以上的定理其实我们都是不知不觉无意识的在使用它们了,在中国这是显然的经验,在使用这些定理时我们自己都没有意识到。西方人不这么干,他把这些不知不觉无意识使用的经验拿出来用公理化思想证明,形成一个极其严密不是松散的系统。这造就了西方发达的科技。 如果我们不学习其实同学们在证明命题时自己自动会使用它们,连自己都没有意识到。因为太显然了,比公理还显然,太常识了,以至于我们没有注意它们,是熟视无睹啊。 我们为什么要学习这几个定理就是让无意识的东西进入我们的意识。
如果同学们还想知道公理系统更多的有关知识,请百度:公理系统的相容性、独立性和完备性。 或百度百科:几何公理体系的基本问题,地址链接:%E5%87%A0%E4%BD%95%E5%85%AC%E7%90%86%E4%BD%93%E7%B3%BB%E7%9A%84%E5%9F%BA%E6%9C%AC%E9%97%AE%E9%A2%98/5557001?fr=aladdin。 如果还想了解更多,请百度百科:哥德尔不完备性定理。链接地址:%E5%93%A5%E5%BE%B7%E5%B0%94%E4%B8%8D%E5%AE%8C%E5%85%A8%E6%80%A7%E5%AE%9A%E7%90%86/4116640?frmtitle=%E5%93%A5%E5%BE%B7%E5%B0%94%E4%B8%8D%E5%AE%8C%E5%A4%87%E5%AE%9A%E7%90%86&frmid=11039894&fr=aladdin。
例1、求证:空间四边形相邻两边中点的连线,平行于经过另两边的平面。
已知:空间四边形ABCD中,E、F分别是AB、AD的中点。 求证:EF ∥ 平面BCD
分析:EF在面BCD外,要证明EF∥面BCD,只要证明EF和面BCD内一条直线平行即可。EF和面BCD哪一条直线平行呢?连结BD立刻就清楚了。
例2 如图,四面体ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点.
(3)你能说出图中满足线面平行位置 关系的所有情况吗?
(1)E、F、G、H四点是否共面?
(2)试判断AC与平面EFGH的位置关系;
解:(1)E、F、G、H四点共面。
∵在△ABD中,E、H分别是AB、AD的中点.
EH ∥GF且EH=GF
∴E、F、G、H四点共面。
(2) AC ∥平面EFGH
(3)由EF ∥HG ∥AC,得
由BD ∥EH ∥FG,得
反思:其实例1、例2题目类似,因为把空间四边形添加几条边就能成为四面体。我们这么安排是想做到精解一题,通一大片,达到举一反三,一通百通的目的。
2.如图,四棱锥A-DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点. 求证: AB//平面DCF.
反思:同学们,这个图你能画出来吗?立体几何题,如果你能画出图,那一般就会证出来。今天因为我们接触立体几何不久,所以先给出成图。
如图,正方体 中,P 是棱 的中点,过点 P 画一条直线使之与截面 平行.
1.证明直线与平面平行的方法:
2.数学思想方法:转化的思想
(1)如果一条直线和一个平面平行,那么这条直线和这个平面内的直线有怎样的位置关系?
(2)已知直线 a∥平面α,如何在平面α内找出和直线a 平行的一条直线?
如果一条直线与一个平面平行,能推出哪些结论呢?这就是要研究直线与平面平行的性质,也就是研究直线与平面平行的必要条件.
假设a与α内的直线b平行,那么由基本事实的推论3,过直线a,b有唯一的平面β.这样,我们可以把直线b看成是过直线a的平面β与平面α的交线.
直线和平面平行的性质定理
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
1、定理三个条件缺一不可。
2、简记:线面平行,则线线平行。
同学们,虽然这个定理是从生活生产实践中总结出来也是比较非常显然比较非常明显的,是我们发现的,但它不是公理而是定理,因为我们可以把它证明出来。 同学们有没有发现西方人没事找事做,吃饱了撑着?正因为西方人的这种刨根究底的精神造就了西方发达的科学。在中国这些是经验,没有证明的迹象。
同学们,书上只介绍了三个基本事实即公理,为什么? 那是因为要建立立体几何公理系统,有这三个公理就足够了,其它都可以把它推导出来,可以当推论或当性质等。其实加上公理4就真的够了,其他任何事实都可以由着四个公理加平面几何的公理和定理推导出来。
例题1 有一块木料,棱BC平行于面A'C' (1)要经过面A'C'内一点P和棱BC锯开木料,应该怎样画线? (2)这线与平面AC有怎样的关系?
例题2 已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面。
注:同学们拿两支笔当直线,把桌面当平面做实验看看,这性质显然不显然?
同学们这个结论实在是太明显太显然了,比公理3还显然,但注意它不是公理而是可以证明出来的性质,这在平时的证明中可以当定理使用。注意我们证明题目时的论据都是来自于教材,教材之外的不会考到,虽然教材之外补充了许多定理、性质。 同学们有没有发现西方人没事找事做,吃饱了撑着?正因为西方人的这种刨根究底的精神造就了西方发达的科学。在中国这些是经验,没有证明的迹象。
转化是立体几何的一种重要的思想方法
利用相似三角形对应边成比例及平行线分线段成比例的性质
如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行。
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.
数学必修 第二册8.5 空间直线、平面的平行教案配套ppt课件: 这是一份数学必修 第二册8.5 空间直线、平面的平行教案配套ppt课件,共29页。PPT课件主要包含了图形语言,定理理解,符号语言,平行或异面,平行或相交,定理作用,典型例题分析,主要利用中位线定理,小结及随堂练习等内容,欢迎下载使用。
人教A版 (2019)必修 第二册8.5 空间直线、平面的平行优秀ppt课件: 这是一份人教A版 (2019)必修 第二册8.5 空间直线、平面的平行优秀ppt课件,共26页。PPT课件主要包含了学习目标,新知学习,易错辨析,典例剖析,随堂小测,ACD,课堂小结等内容,欢迎下载使用。
人教A版 (2019)必修 第二册8.5 空间直线、平面的平行教学课件ppt: 这是一份人教A版 (2019)必修 第二册8.5 空间直线、平面的平行教学课件ppt,共29页。PPT课件主要包含了答案D,答案B,答案5等内容,欢迎下载使用。














