




高中8.6 空间直线、平面的垂直课文内容课件ppt
展开同学们,在直线、面的各种位置关系中,平行和垂直是最重要的关系。前面几节课我们学习了线、面平行的各种位置关系,得到了判定定理和性质定理。下面我们先梳理下空间直线、平面平行的研究过程。
18世纪的法国有一个农民家庭出身的数学家和天文学家——拉普拉斯(Pierre—Simn de laplace1749—1827)。拉普拉斯是现代概率论的奠基者之一。学物理的人对他很熟。 他有一个很好的品德,就是对于年青一代的数学家当作自己的孩子,帮助他们和鼓励他们。有一些人的发现事实上是他早在几十年前就得到了,但他也是把这发现的荣誉让给年青人而不是自己占有、不像一些所谓“专家”对这些新生的力量,在妒忌之余,加以阻挠打击。 拉普拉斯在关于概率论的哲学问题的一篇文章里曾经指出:“在数学这门科学里,我们发现真理的主要工具是归纳和类比(inductin and analgy)。”这里他指出了发现数学定理的一个方法。
类比线、面平行的位置关系,我们可以照着学习直线、面的垂直的位置关系,来探讨它的判定定理和性质定理,这是依葫芦画瓢。
但正确的研究过程其实与上述的研究过程稍微有点出入。正确的研究过程是下面的流程图。
空间两直线的位置关系:
(1)从公共点的数目来看可分为: ①有且只有一个公共点则 两直线相交 两平行直线 ②没有公共点则 两直线为异面直线
(2)从是否共面来讲,可分为: 两直线相交 ①在同一平面内 两直线平行 ②不在任一平面内则两直线为异面直线。
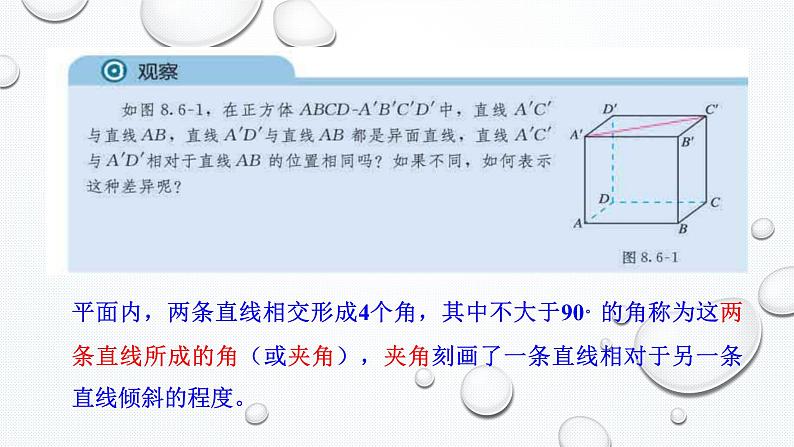
平面内,两条直线相交形成4个角,其中不大于90。的角称为这两条直线所成的角(或夹角),夹角刻画了一条直线相对于另一条直线倾斜的程度。
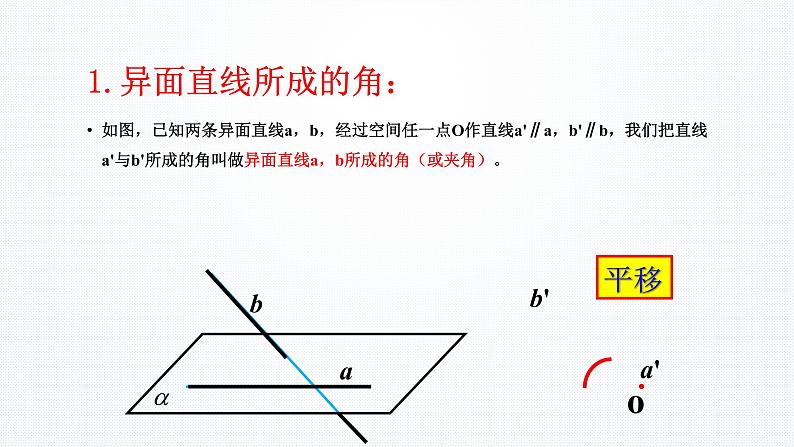
1.异面直线所成的角:
如图,已知两条异面直线a,b,经过空间任一点O作直线a'∥a,b'∥b,我们把直线a'与b'所成的角叫做异面直线a,b所成的角(或夹角)。
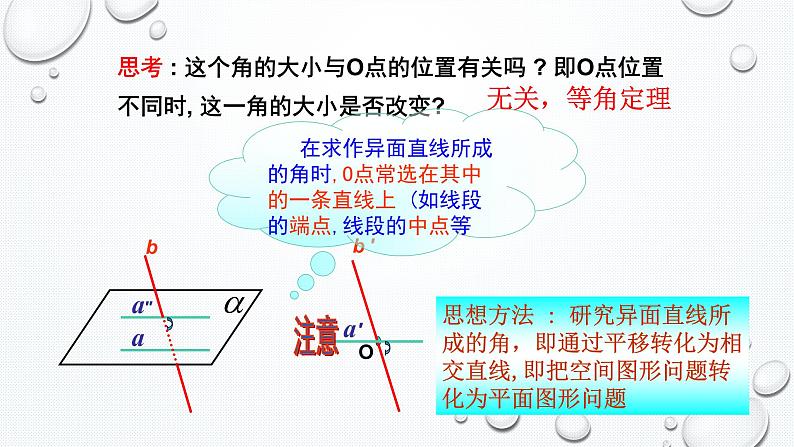
思考 : 这个角的大小与O点的位置有关吗 ? 即O点位置不同时, 这一角的大小是否改变?
思想方法 : 研究异面直线所成的角,即通过平移转化为相交直线,即把空间图形问题转化为平面图形问题
2.异面直线所成角的范围:
如果两条异面直线所成的角是直角,那么我们就说这两条直线互相垂直。直线a与b垂直,记作 a⊥b
空间两条直线垂直,它们一定相交吗?
思考:(1)如果两条平行直线中的一条与某一条直线垂直,那么另一条直线是否也与这条直线垂直?
(2)在同一平面内垂直于同一条直线的两条直线平行,那么在空间中这一结论是否仍然成立?
我们规定:两条平行直线的夹角为 :
空间两条直线所成角 的取值范围是:
那么,两条异面直线所成的角 的取值范围是:
答:顾名思义就可以了。
3.异面直线所成的角、线线垂直的应用
例1.已知正方体ABCD-A′B′C′D′(1)哪些棱所在的直线与直线AA′垂直?(2)求直线BA'与CC'所成的角的大小.(3)求直线BA'与AC 所成的角的大小.
解:连接 A′C′ ,
变式训练:如图,已知长方体ABCD-EFGH中,AB =AD = ,AE = 2(1)求BC 和EG 所成的角是多少度?(2)求AE 和BG 所成的角是多少度?
常见的平行关系:1.中位线原理2.平行四边形3.对应边成比例
4.在四面体ABCD中,E、F分别是棱AD、BC上的点,且 ,已知 AB=CD=3,EF= ,求异面直线AB和CD所成的角。
5.在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和B1C1的中点,求直线AM与CN所成角的余弦值
6.正四面体S-ABC中,如果E,F分别是SC,AB的中点,那么异面直线EF与SA所成的角等于( ) (A)90°(B)45°(C)60°(D)30°
作业:1.课本 P148 1,2,3,4 ;P162 4,5,112.准备一块三角形的纸片
今天所讲的知识你学会了吗?
如果你学会了,请完成下列作业!
如果你还没学会,请通过下列作业把它学会!
两条异面直线所成的角概念两条异面直线所成的角范围步骤:一作二证三解四结论
空间问题转化为平面问题
高中8.6 空间直线、平面的垂直图文ppt课件: 这是一份高中8.6 空间直线、平面的垂直图文ppt课件,共21页。PPT课件主要包含了面面平行,线线垂直,线面垂直,面面垂直,有区别,都是异面直线,“歪”的程度不一样,使两条直线相交共面,选择较小角来刻画,空间中两直线垂直等内容,欢迎下载使用。
人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直完美版课件ppt: 这是一份人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直完美版课件ppt,共27页。PPT课件主要包含了学习目标,新知学习,易错辨析,典例剖析,异面直线所成的角,反思感悟,跟踪训练,二直线与直线垂直,随堂小测,课堂小结等内容,欢迎下载使用。
人教A版 (2019)必修 第二册第八章 立体几何初步8.6 空间直线、平面的垂直备课课件ppt: 这是一份人教A版 (2019)必修 第二册第八章 立体几何初步8.6 空间直线、平面的垂直备课课件ppt,共21页。














