人教A版 (2019)选择性必修 第一册1.1 空间向量及其运算图文课件ppt

这是一份人教A版 (2019)选择性必修 第一册1.1 空间向量及其运算图文课件ppt，共37页。PPT课件主要包含了回顾引入1平面向量，表示法，向量加法的三角形法则，向量的数乘，首尾相接首尾连，共起点对角线，回顾引入，加法交换律，加法结合律，数乘运算律等内容，欢迎下载使用。

我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”．数学中，数和形是两个最主要的研究对象，它们之间有着十分密切的联系，在一定条件下，数和形之间可以相互转化，相互渗透．
而向量却是数形完美结合体。向量既是代数研究对象也是几何研究对象，它是沟通代数与几何的桥梁。因为大小属于代数，方向属于几何。
数学家华罗庚提出了科研的四种境界：第一种是照葫芦画瓢模仿．刚开始做科研的人习惯于模仿参考文献做一些小小的改进和推广，没有什么创新．第二种境界是对现有的方法进行改进用来解决新问题或对现有方法进行修补以更好地解决老问题．这和第一种境界没有太大的区别，但这样做时，由于现有方法并不完全适用于新问题，还是有一些改进工作要做的.而且，在用老方法尝试解决新问题的时候可能会产生新的思路．所以，我们不要小瞧这样的工作. 著名数学家陈景润“1+2”的研究成果就是利用挪威数学家布朗的“筛法”得到的．但一个人做数学研究不能老局限在这种“攀亲”的境界里，而要考虑针对新问题有无更有效的方法．这就引出了做科研的第三种境界：用创新性的方法解决新问题或老问题．这种境界完全有别于前两种境界，是创造力提高的表现．科研的第四种境界是开辟新领域、新方向．这种拓荒探宝性的工作，其意义不言而喻．它要求很高，一般人也很难达到．
而向量方法就属于科研的第三境界。
李邦河院士说：“根据我上大学以后搞数学研究的经验，数学根本上是玩概念，不是玩技巧。技巧不足道也！”
我们知道数学来自于生活生产实践，数学上的每个概念都有现实的生活原型。数学家是考察了生活生产中的各种现象，发现这些现象有共同的模型，于是提炼出来得到数学上的一个概念。这也说明学习数学就是学习数学化。马克思说理论来源于实践，但理论对实践具有反作用或能动作用。马克思唯物主义有个原则物质决定意识，但意识对物质具有反作用或能动作用。我们经常说的话是没有理论的实践是盲目的，没有实践的理论是空洞的。
比如数学家提出向量概念，得到一套向量理论，按向量理论解决了许多数学问题。
那在生活生产实践中哪些是向量的原型呢？
百度：“向量”的前世今生：8位天才数学家，耗时2000年完成 
平面内既有大小又有方向的量。
3、共线向量或平行向量
4、零向量及其性质和单位向量
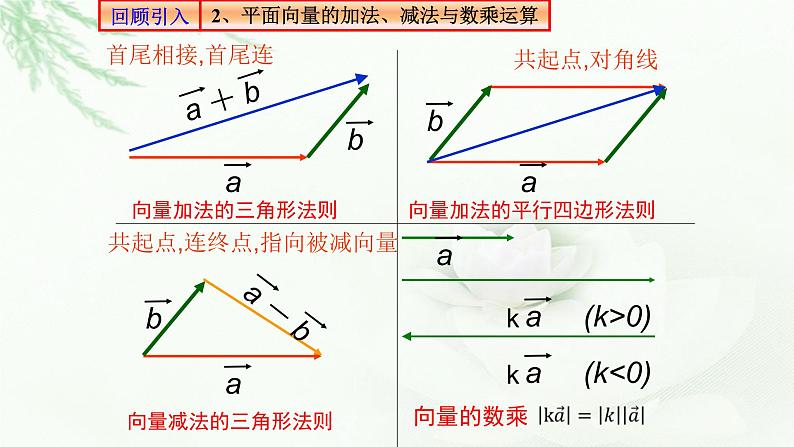
2、平面向量的加法、减法与数乘运算
向量加法的平行四边形法则
共起点,连终点,指向被减向量
3、平面向量的加法、减法与数乘运算律
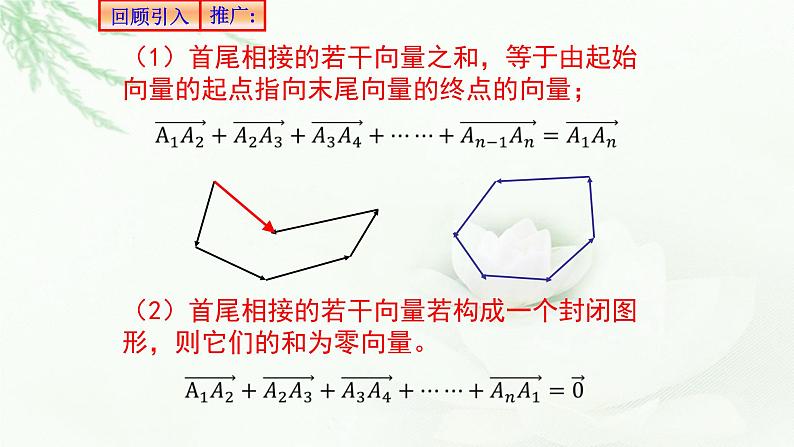
（1）首尾相接的若干向量之和，等于由起始向量的起点指向末尾向量的终点的向量；
（2）首尾相接的若干向量若构成一个封闭图形，则它们的和为零向量。
1、如何学习本节知识？
答：不是死记硬背，而是顾名思义。
2、向量的符号、模的符号、线段符号、线段的长度符号、有向线段的大小方向符号会不会混淆？
3、为什么规定零向量的方向是任意的 。
4、平行向量与共线向量是一回事说明平移不改变向量的大小和方向，平移不改变向量的任何内含，向量平移后还是原来的向量。
答：高中数学知识是属于几百年之前的事了，几百年之前的数学发展到现在是非常完美了，所以同学们不用担心符号会混淆，只要我们看到一个数学符号其实马上就知道是什么东西。
我能不能这样解释?假如规定零向量的方向是向东,那也可以规定零向量的方向是向西、向南、向北，所以干脆就规定是任意。
反思1：向量加法有三角形法则与平行四边形法则，数学上为什么要这样规定？我那样规定不行吗？注意什么？
答：数学上的定义、规定不是胡来的，而是有深刻的现实基础，既然有深刻的现实基础，所以数学就能解决许多现实问题。马克思主义认为理论来源于实践又对实践具有反作用或能动作用。 三角形法则是向量首尾相接再首尾相连，平行四边形法则是起点重合。
反思2 1、向量加法满足交换律与结合律的证明根据什么只能根据什么？ 答：向量加法的定义 2、数的大小可正可负，那向量的模只能是正的或等于0，请问模的符号好不好？这个符号会让你产生模是负的嫌疑吗？ 答：符号形象生动，只要与数的绝对值联系起来就可以理解。 3、在书写向量的时候记住一条，也就是符号要让人一看就知道是什么含义不要让人误会和嫌疑。举个例子零向量的书写。符号都是数学家创造出来的，是禁得起历史的考验。数学家都是天才。 4、符号表达向量的加法要知道有两层意义在运算，一层是大小的运算，一层是方向的运算。 5、实数满足交换律和结合律你觉得向量满足吗？为什么？ 答：世界是和谐的，虽然有时候无奇不有。如果不满足，世界的和谐美被破坏掉，令人不舒服。但越到高维越奇异，比如四元数。四元数（Quaternins）是由爱尔兰数学家哈密顿(William Rwan Hamiltn,1805-1865）在1843年发明的数学概念。四元数的乘法不符合交换律（cmmutative law）。大家百度：四元数 6、两向量相加如果不共线则用三角形法则或平行四边形法则，但有种情况要区别对待那就是共线，而共线又分成同向和反向但也是首位相连也符合三角形法则。
我们看到向量的减法可以转化为加法进行计算。减去一个向量等于加上这个向量的相反向量。
我的观点：那就是再使用三角形法则或平行四边形法则。
教材观点：教材是另起炉灶，探索向量减法的几何意义。有的同学可能会一团乱麻，向量加法减法死死分不清。那你就不要去学习向量减法的几何意义了，因为越学越糊涂。
上图中方块受到各种方向的力，这些力不在同一平面内。联想用平面向量解决物理问题的方法，能否把平面向量推广到空间向量，从而利用空间向量来解决自然界的物理问题。 下面我们用类比的方法把平面向量推广为空间向量。我们先把平面向量有关概念及线性运算推广为空间向量有关概念及线性运算。下节课再把平面向量的数量积、正交分解、坐标表示、运算的坐标推广到空间向量的数量积、正交分解、坐标表示、运算的坐标。 我们看看在推广时，哪些内容需要改变，哪些内容可以原封不动的照搬。
空间中既有大小又有方向的量
2、空间向量的表示方法。
３、什么样的向量是相等的向量？
4、空间内零向量、空间内单位向量。5、空间内共线向量或平行向量
结论：空间任意两个向量都是共面向量，所以它们可用同一平面内的两条有向线段表示。因此凡是涉及空间任意两个向量的问题，平面向量中有关结论仍适用于它们。
思考：它们确定的平面是否唯一？
思考：空间任意两个向量是否可能异面？
2.空间向量的加法、减法向量
因为平移不改变向量的大小和方向，所以空间向量的加减可以转化为平面向量的加减。空间中通过平移任何两向量都共面
a + b = b + a；
(a + b) + c =a + (b + c)；
为什么在空间向量的运算律依然成立那就是在证明运算律时下图即可以看成平面图形也可以看成空间图形。
对空间向量的加法、减法的说明
⒈空间向量的运算就是平面向量运算的推广．
⒉两个向量相加的平行四边形法则在空间仍　然成立．
⒊空间向量的加法运算可以推广至若干个向　量相加．
⑴首尾相接的若干向量之和，等于由起始向量的起点指向末尾向量的终点的向量．即：
此图即可以看成平面图形也可以看成空间图形。所以平面内向量的结论依然在空间成立。
⑵首尾相接的若干向量构成一个封闭图形，则它们的和为零向量．即：
记作ABCD—A1B1C1D1，它的六个面都是平行四边形，每个面的边叫做平行六面体的棱。
同学们注意平行六面体有另外种生成方式，即换个角度看平行六面体。
例1：已知平行六面体ABCD-A1B1C1D1,化简下列向量表达式,并标出化简结果的向量.(如图)
始点相同的三个不共面向量之和，等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所示向量
下面我们看看在平面向量中，我们是如何学习的？可以原封不动的推广为空间向量中去吗？
①问学习数学是记住定理然后去套吗？答：不是记住定理去套，而是要深刻理解定理的本质，看到这定理要想起上述四种情况。如果去套一般考个高职或专科。
实数与向量积的运算律在空间中依旧成立。
反思：平面向量基本定理到了空间就变成空间向量共面定理。
平面向量基本定理
例2 (课本例)已知 ABCD ，从平面AC外一点O引向量
求证：①四点E、F、G、H共面；
②平面EG //平面AC.
所以 E、F、G、H共面。
由面面平行判定定理的推论得：
同学们，此题你会用几何法证明吗？