






人教A版 (2019)选择性必修 第一册1.4 空间向量的应用示范课ppt课件
展开从今天开始,我们将进一步来体会向量这一工具在立体几何中的应用.
三、1、同学们还记得直线或线段在一个平面内的投影吗?它是什么?线段的长度有什么改变? 2、在一个平面内一条线段在一条直线上的投影是怎样子的?线段的长度有什么改变? 3、那向量在另一个向量上的投影是怎么回事? 答:线段只有大小没有方向,所以投影肯定是正的,但向量是即有大小又有方向,所以大小、方向都有投影。那如何表示方向的投影?请同学们看看向量投影的定义。
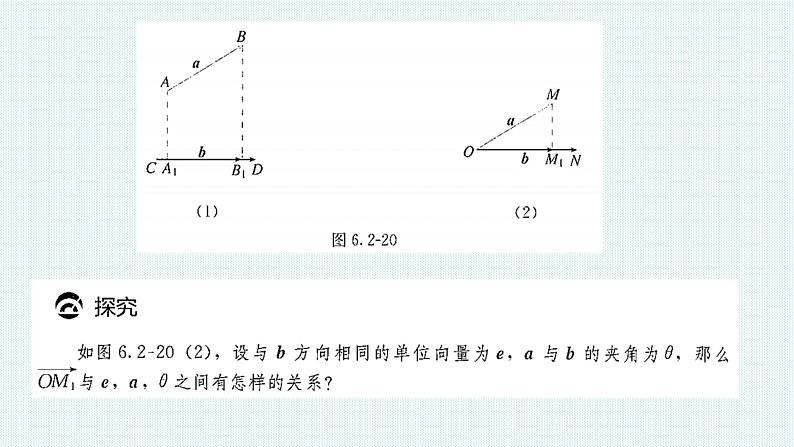
将空间向量a,b ,平移到同一个平面α内,利用平面上向量的投影得到与向量b共线的向量c,即: c =|a|cs〈a,b〉 , 向量c称为向量a在向量b上的投影向量.
以上是我们在平面向量中我们学习过投影向量的概念,你能把它推广到空间向量中吗?
反思:1、如果不懂在空间中向量在另一向量上的投影怎办?
答:不是努力去搞懂,而是要回到过去即最初的那个地方,也就是去搞懂在平面内向量在另一向量上的投影定义,把平面内的定义搞懂了,自然就会把空间内的定义搞懂。有种方法叫回到定义中去,即最开始的那个原点。
点P 到直线l的距离为PQ =
点到直线的距离、两条平行直线之间的距离
2.两条平行直线之间的距离求两条平行直线l,m之间的距离,可在其中一条直线l上任取一点P,则两条平行直线间的距离就等于点P到直线m的距离.
已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是C1C, D1A1的中点,则点A到直线EF的距离为 .
向量法求点到平面的距离:
点到平面的距离、两个平行平面之间的距离
这个结论说明,平面外一点到平面的距离等于连结此点与平面上的任一点(常选择一个特殊点)的向量在平面的法向量上的射影的绝对值.请看解法②。
平面外一点到平面的距离等于连结此点与平面上的任一点(常选择一个特殊点)的向量在平面的法向量上的射影的绝对值.
直线和平面间的距离:如果一条直线l与一个平面α平行,可在直线l上任取一点P,将线面距离转化为点P到平面α的距离求解.两个平行平面之间的距离如果两个平面α,β互相平行,在其中一个平面α内任取一点P,可将两个平行平面的距离转化为点P到平面β的距离求解.
在正四棱柱ABCD-A1B1C1D1中,底面边长为2,侧棱长为4,则点B1到平面AD1C的距离为 .
解析:以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,则A(2,0,0),C(0,2,0),D1(0,0,4),B1(2,2,4),
例1已知直三棱柱ABC-A1B1C1中,AA1=1,AB=4,BC=3,∠ABC=90°,求点B到直线A1C1的距离.
解:以B为坐标原点,建立如图所示的空间直角坐标系,则A1(4,0,1),C1(0,3,1),所以直线A1C1的方向向量
所以点B到直线A1C1的距离
用向量法求点到直线的距离时需注意以下几点:(1)不必找点在直线上的垂足以及垂线段;(2)在直线上可以任意选点,但一般选较易求得坐标的特殊点;(3)直线的方向向量可以任取,但必须保证计算正确.
例2: 如图,已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.
分析:用几何法做相当困难,注意到坐标系建立后各点坐标容易得出,又因为求点到平面的距离可以用法向量来计算,而法向量总是可以快速算出.
反思:此类题典型的说明了向量法与几何法各有什么优劣。结合前面几节课的内容。 几何法:缺点:几何法复杂难懂,需要空间想象能力超强。几何法思维的发生发展难,几何法技巧性高个性强,很不容易想到。 优点:几何法证(求)出来了我们就知道为什么能证(求)出来,几何法能看清几何体的结构本质。几何法是垂直我们就知道为什么垂直,因为有图形为证。也因为几何法我们是通过视觉,向量法却是大脑的抽象思维。 向量法:优点:向量法简单明了没几步。此题可看出向量法的威力和优越。向量法是证出来了也不知道为什么能证出来。向量法表面上是代数运算实际上是几何运算,几何运算被隐藏起来了。向量法证明是空荡荡的,找不到一个坚实的支撑点。向量法看不清楚。 结合前几节课的题可看出向量法是只披着羊皮的狼。向量法求解与证明可以有统一的模式,几何法却是技巧性高个性强。 缺点:运算量很大。
用空间向量解决立体几何问题的“三步曲”。
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何意义。
人教A版 (2019)选择性必修 第一册1.4 空间向量的应用获奖课件ppt: 这是一份人教A版 (2019)选择性必修 第一册1.4 空间向量的应用获奖课件ppt,共47页。PPT课件主要包含了常考题型,解题方法等内容,欢迎下载使用。
高中人教A版 (2019)1.4 空间向量的应用优秀课件ppt: 这是一份高中人教A版 (2019)1.4 空间向量的应用优秀课件ppt,共34页。PPT课件主要包含了一两个平面的夹角,不大于90°,即时巩固,因此CM⊥SN,反思感悟,两个平面的夹角等内容,欢迎下载使用。
人教A版 (2019)选择性必修 第一册1.4 空间向量的应用试讲课ppt课件: 这是一份人教A版 (2019)选择性必修 第一册1.4 空间向量的应用试讲课ppt课件,共25页。PPT课件主要包含了即时巩固,点到直线的距离,x+y+z=1等内容,欢迎下载使用。














