人教A版 (2019)选择性必修 第一册2.3 直线的交点坐标与距离公式图片课件ppt

这是一份人教A版 (2019)选择性必修 第一册2.3 直线的交点坐标与距离公式图片课件ppt，共27页。PPT课件主要包含了x1y0，思路一，利用两点间距离公式，思路二，点到直线的距离，化为一般式等内容，欢迎下载使用。

解析几何是17世纪最伟大的数学成果之一，它的产生有着深刻的原因．　　首先，生产力的发展对数学提出了新的要求，常量数学的局限性越来越明显了．例如，航海业的发展，向数学提出了如何精确测定经纬度的问题；造船业则要求描绘船体各部位的曲线，计算不同形状船体的面积和体积；显微镜与望远镜的发明，提出了研究透镜镜面形状的问题；随着火器的发展，抛射体运动的性质显得越来越重要了，它要求正确描述抛射体运动的轨迹，计算炮弹的射程，特别是开普勒发现行星沿椭圆轨道绕太阳运行，要求用数学方法确定行星位置．所有这些问题都难以在常量数学的范围内解决．实践要求人们研究变动的量．解析几何便是在这样的社会背景下产生的．
总结：在当时，以前的几何是定性研究不是定量研究，不是精确的计算。同学们，平面几何或立体几何中有精确的计算吗？没有。只有向量进入几何才有精确计算。但向量比解析几何更晚。
其次，解析几何的产生也是数学发展的大势所趋，因为当时的几何与代数都相当完善了．实际上，几何学早就得到比较充分的发展，《几何原本》建立起完整的演绎体系，阿波罗尼奥斯的《圆锥曲线论》则对各种圆锥曲线的性质作了详尽的研究．但几何学仍存在两个弱点，一是缺乏定量研究，二是缺乏证题的一般方法．而当时的代数则是一门注重定量研究、注重计算的学科．到16世纪末，韦达(F．Vieta， 1540—1603)在代数中有系统地使用字母，从而使这门学科具有了一般性．它在提供广泛的方法论方面，显然高出希腊人的几何方法．于是，从代数中寻求解决几何问题的一般方法，进行定量研究，便成为数学发展的趋势．实际上，韦达的《分析术引论》(In artem analyticem isagge)等著作中的一些代数问题，便是为解几何题而列出的．
点到直线的距离公式就是可以精确的计算距离。那它该如何推导？
我们知道人的认识规律是从特殊到一般，从具体到抽象，从数字到字母，从简单到复杂。只要特殊熟练了，就能上升到一般。只要具体熟练了，就能上升到抽象，只要数字熟练了，就能上升到字母。只要简单熟练了，就能做复杂的题目。
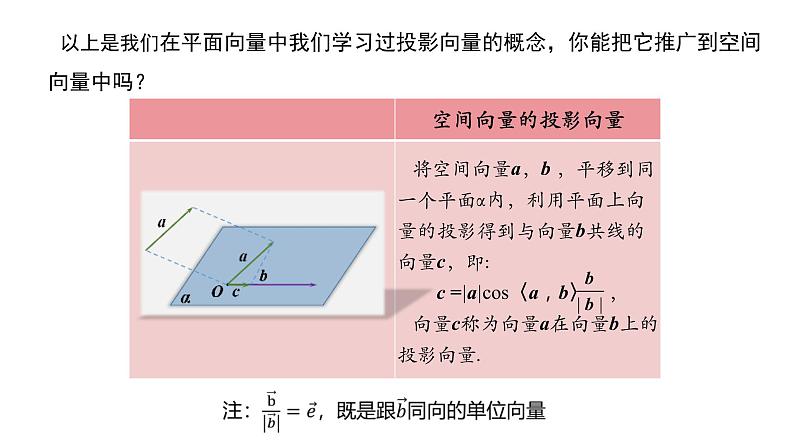
将空间向量a，b ，平移到同一个平面α内，利用平面上向量的投影得到与向量b共线的向量c，即: c =|a|cs〈a，b〉 ， 向量c称为向量a在向量b上的投影向量.
以上是我们在平面向量中我们学习过投影向量的概念，你能把它推广到空间向量中吗？
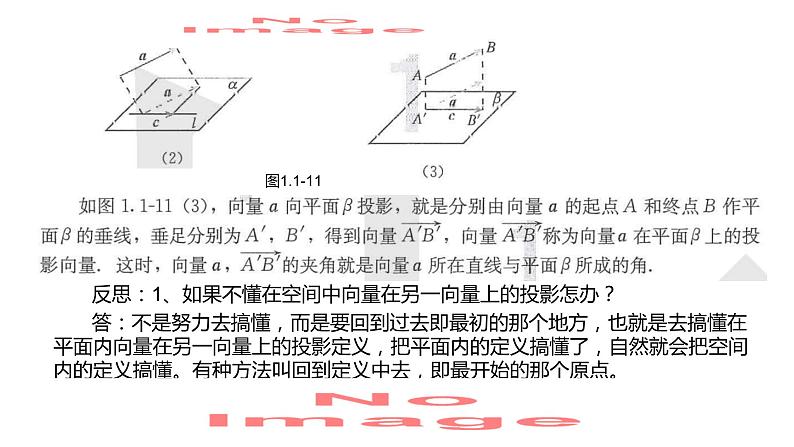
反思：1、如果不懂在空间中向量在另一向量上的投影怎办？
答：不是努力去搞懂，而是要回到过去即最初的那个地方，也就是去搞懂在平面内向量在另一向量上的投影定义，把平面内的定义搞懂了，自然就会把空间内的定义搞懂。有种方法叫回到定义中去，即最开始的那个原点。
同学们，如何把点到直线的距离从特殊推广为一般？
思考：已知点P0(x0,y0)和直线l:Ax+By+C=0, 怎样求点P到直线l的距离呢?
如图，P到直线l的距离，就是指从点P到直线l的垂线段PQ的长度，其中Q是垂足.
当A=0或B=0时,直线方程为y=y1或x=x1的形式.
下面设A≠0,B ≠0,我们进一步探求点到直线的距离公式:
点P到直线/的距离，就是从点P到直线/的垂线段PQ的长度，其中Q是垂足(如右图).因此，求出垂足Q的坐标，利用两点间的距离公式求出|PQ|,就可以得到点P到直线l的距离.
得直线l与PQ的交点坐标，即垂足Q的坐标为
因此，点P(x,y)到直线l :Ax+By+C=0的距离
可以验证，当A=0,或B=0时，上述公式仍然成立
利用两点间距离公式，设而不求:
将(1)(2)两边平方后相加，得
我们知道，向量是解决距离、角度问题的有力工具.能否用向量方法求点到直线的距离?
同学们，还记得我们在《1.4.2 用空间向量研究距离、夹角问题》中求点到直线的距离吗？与上述解法有什么区别？
点P 到直线l的距离为PQ =
点到直线的距离、两条平行直线之间的距离
P0(x0,y0)到直线l:Ax+By+C=0的距离：
（1）分子是P点坐标代入直线方程；
（2）分母是直线未知数x、y系数平方和的算术根
类似于勾股定理求斜边的长
(3)运用此公式时要注意直线方程必须是一般式, 若给出其他形式,应先化成一般式再用公式.(4)当点P0在直线l上时,点到直线的距离为零,公式仍然适用.
例1:已知点A(1,3),B(3,1),C(-1,0)，求△ABC的面积
解：设AB边上的高为h
例2：用解析法证明：等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高。
证明:建立如图直角坐标系,设P (x,0),x∈( )
可求得lAB:( )
lCB:( )
|PE|=( )
|PF|=( )
A到BC的距离h=( )
因为|PE|+|PF|=h，所以原命题得证。
复习：还记得初中里的证法吗？
例3.已知直线l经过点M(-1,2),且A(2,3),B(-4,5)两点到直线l的距离相等,求直线l的方程.
已知直线l经过点M(-1,2),且A(2,3),B(-4,5)两点到直线l的距离相等,求直线l的方程.
求经过点P(-3,5),且与原点距离等于3的直线l的方程
在根据距离确定直线方程时,易忽略直线斜率不存在的情况,避免这种错误的方法是当用点斜式或斜截式表示直线方程时,应首先考虑斜率不存在的情况是否符合题设条件,然后再求解.
1.平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式是
当A=0或B=0时,公式仍然成立.
2.点到直线的距离即是点与直线上点连线的距离的最小值，利用点到直线的距离公式，解题时要注意把直线方程化为一般式. 3.利用点到直线的距离公式可求直线的方程，有时需结合图形，数形结合，使问题更清晰.
备课笔记 今天（2021.4.5）开始备选择性必修第一册《第二章 直线和圆的方程》，下载了一些老师制作的课件，翻出自己以前制作的课件。我以前制作的课件都存在百度文库里。我在感叹，如果不上讲台，备课永远无法超越自己。这一章备课我觉得还是跟以前一样，只有上讲台才能有所改变。因为实践出新知，你坐在办公室里空想是想不出来的。 这一章如何上？有个观点，就是站在人类文明的高度上解析几何课。我们要站在人类文明的数学星空里讲数学、观数学、知数学。学习数学不是考个高分找个好工作，而是体会到数学在整个人类文明中的地位，和对人类的巨大影响。学习不是功利性，而是要超越功利，追求人类永恒的精神。