高中数学人教A版 (2019)选择性必修 第一册2.5 直线与圆、圆与圆的位置教课内容ppt课件

这是一份高中数学人教A版 (2019)选择性必修 第一册2.5 直线与圆、圆与圆的位置教课内容ppt课件，共34页。PPT课件主要包含了第二课时等内容，欢迎下载使用。
一、我们知道，在笛卡尔之前，几何和代数是老死不相往来，各自分开。是笛卡尔让几何代数联系在一起。也就是通过直角坐标系。笛卡儿向世人证明，几何问题可以归结成代数问题，也可以通过代数转换来发现、证明几何性质。 其实笛卡尔曾经有个伟大构想，那就是：把一切问题归结为数学问题，把一切数学问题归结为代数问题，把一切代数问题归结为方程，最后得到关于一个未知数的方程。只要把这个方程解出来，就解决了任何问题。我们知道按当代科技这个构想是不能实现的。比如化学、生物学科。就算是数学也不能都归结为方程问题。 把几何问题归结成代数问题这是个很新鲜的想法。 比如点有个坐标，但直线由点组成，所以直线是否有代数形式，这很新鲜的。我们知道在几何中两直线由相交、平行，那反应在代数上会是怎么回事，也是很新鲜的。在几何中有圆，那圆的代数形式是怎样的，在几何中直线与圆有好几种关系，这几种关系如果从代数角度讲会有新鲜的结论吗？ 这节课我们讲直线的代数形式，那就是直线的方程。这是很新鲜的东西，在笛卡尔之前是没有的。
解析几何是17世纪最伟大的数学成果之一，它的产生有着深刻的原因．　　首先，生产力的发展对数学提出了新的要求，常量数学的局限性越来越明显了．例如，航海业的发展，向数学提出了如何精确测定经纬度的问题；造船业则要求描绘船体各部位的曲线，计算不同形状船体的面积和体积；显微镜与望远镜的发明，提出了研究透镜镜面形状的问题；随着火器的发展，抛射体运动的性质显得越来越重要了，它要求正确描述抛射体运动的轨迹，计算炮弹的射程，特别是开普勒发现行星沿椭圆轨道绕太阳运行，要求用数学方法确定行星位置．所有这些问题都难以在常量数学的范围内解决．实践要求人们研究变动的量．解析几何便是在这样的社会背景下产生的．
总结：在当时以前的几何是定性研究不是定量研究，不是精确的计算。同学们平面几何或立体几何中有精确的计算吗？没有。在空间向量与立体几何中有精确的计算，但向量比解析几何出现得更晚。
其次，解析几何的产生也是数学发展的大势所趋，因为当时的几何与代数都相当完善了．实际上，几何学早就得到比较充分的发展，《几何原本》建立起完整的演绎体系，阿波罗尼奥斯的《圆锥曲线论》则对各种圆锥曲线的性质作了详尽的研究．但几何学仍存在两个弱点，一是缺乏定量研究，二是缺乏证题的一般方法．而当时的代数则是一门注重定量研究、注重计算的学科．到16世纪末，韦达(F．Vieta， 1540—1603)在代数中有系统地使用字母，从而使这门学科具有了一般性．它在提供广泛的方法论方面，显然高出希腊人的几何方法．于是，从代数中寻求解决几何问题的一般方法，进行定量研究，便成为数学发展的趋势．实际上，韦达的《分析术引论》(In artem analyticem isagge)等著作中的一些代数问题，便是为解几何题而列出的．
在初中平面几何中我们学习了直线与圆的位置关系。我们知道初中的平面几何是属于笛卡尔时代之前的数学知识。当笛卡尔把几何与代数联系起来时，我们看看用代数角度研究直线与圆的位置关系看看有什么新鲜的结论或有什么不同的风景，又多了些什么，并且直线与圆的位置关系可以精确的计算吗？这在平面几何中是不可能的事情，就算有也是比较肤浅的，比如直接给出d、r。 我们知道笛卡尔之前几何、代数是相互分离，老死不相往来的。
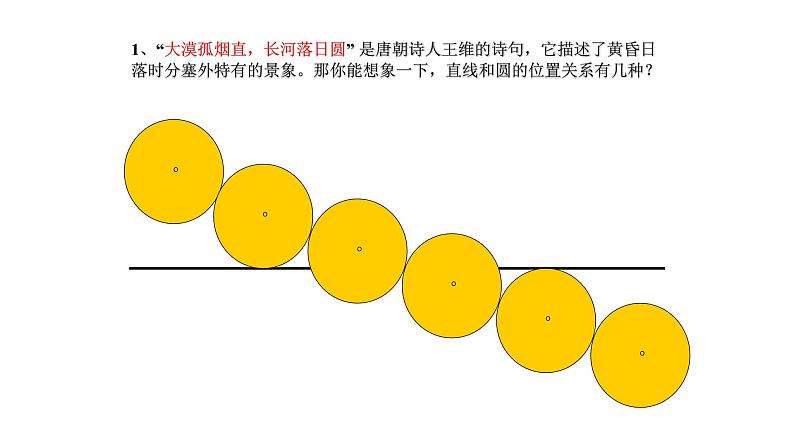
1、“大漠孤烟直，长河落日圆” 是唐朝诗人王维的诗句，它描述了黄昏日落时分塞外特有的景象。那你能想象一下，直线和圆的位置关系有几种？
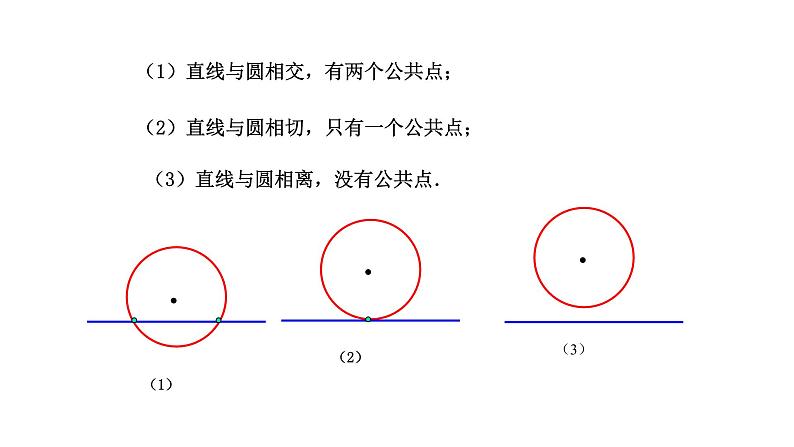
（1）直线与圆相交，有两个公共点；
（2）直线与圆相切，只有一个公共点；
（3）直线与圆相离，没有公共点．
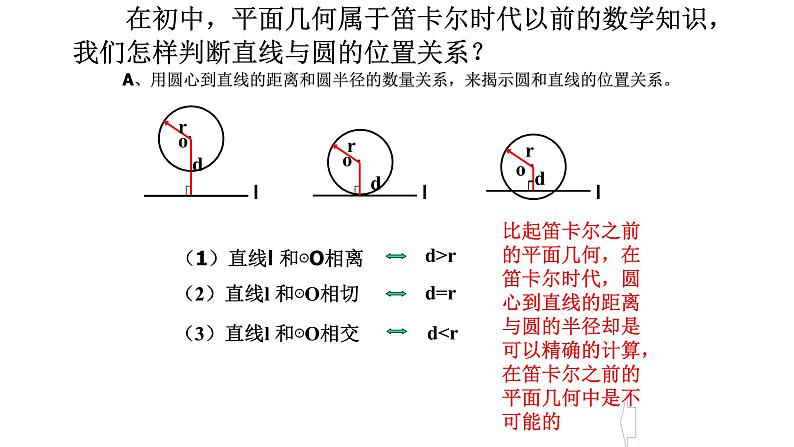
（2）直线l 和⊙O相切
A、用圆心到直线的距离和圆半径的数量关系，来揭示圆和直线的位置关系。
（1）直线l 和⊙O相离
（3）直线l 和⊙O相交
比起笛卡尔之前的平面几何，在笛卡尔时代，圆心到直线的距离与圆的半径却是可以精确的计算，在笛卡尔之前的平面几何中是不可能的
在初中，平面几何属于笛卡尔时代以前的数学知识，我们怎样判断直线与圆的位置关系？
B、高中我们学习的是笛卡尔时代的数学知识，它多了什么来判断直线与圆的位置关系。
1、将直线与圆的方程联立.
2、利用消元法，得到关于另一个元的一元二次方程.
这个就是新鲜的结论和不同的风景，比起笛卡尔之前的平面几何这是多了的判断方法。
答：用方程组的解的个数判断直线和圆的位置关系
(1)利用圆心到直线的距离d与半径r的大小关系判断：
直线与圆的位置关系的判定方法：
直线l：Ax+By+C=0
圆C：(x-a)2+(y-b)2=r2(r>0)
(2) 利用直线与圆的公共点的个数进行判断：
例1、如图，已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0，判断直线l与圆的位置关系；如果相交，求它们的交点坐标及弦长
设C到直线l的距离为d
所以直线l与圆相交有两个公共点
虽然这种判断方法在笛卡尔之前的平面几何中有，但在笛卡尔时代却是可以精确计算的，比如计算圆心是多少、计算圆心到直线的距离是多少。在笛卡尔之前的平面几何中是做不到的。
解：联立圆和直线的方程得
所以方程④有两个不相等的实根x1＝1，x2 ＝2
把x1，x2代入方程③得到y1 ＝3 ，y2 ＝0
所以直线l与圆有两个不同的交点A(1,3),B(2,0)所以弦长
例1、如图，已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0，判断直线l与圆的位置关系；如果相交，求它们的交点坐标及弦长。
这是在笛卡尔时代多了的判断方法。
分析：求弦长还有其它方法吗？
同学们，当几何、代数结合后直线与圆的位置关系可以精确的计算，比如精确的求出直线与圆的交点坐标，也可以精确的求出圆心到弦的距离或弦长。在平面几何中即笛卡尔之前是不可能的
例2.过点P(2,1)作圆O:x2+y2=1的切线l,求切线的方程
分析：如图,容易知道，点P(2,1)位于圆O:x2+y2=1外，经过圆外一点有两条直线与这个圆相切，我们设切线方程为y-1=k(x-2),k为斜率，由直线与圆相切可求出k的值.
解法1:设切线l的斜率为k,则切线l的方程为y-1=k(x-2),即x-y+1-2k=0.由圆心(0,0)到切线l的距离等于圆的半径1,得
解法2:设切线l的斜率为k,则切线l的方程为y-1=k(x-2).因为直线l与圆相切，所以方程组
因此，所求切线l的方程为y=1,或4x-3y-5=0.
所以，所求切线l的方程为y=1,或4x-3y-5=0.
解法2只有在笛卡尔时代才会出现，在笛卡尔之前这解法是没有的。
虽然解题思路在笛卡尔之前的平面几何中有，但在笛卡尔时代却是可以精确计算的，在笛卡尔之前的平面几何中是做不到的。
例3、已知过点M(-3，-3）的直线l被圆x2+y2+4y-21=0所截得的弦长为 ，求直线l的方程。
同学们注意只有在笛卡尔时代直线与圆才可以这样精确计算，在笛卡尔之前即平面几何中这样子是不可能的
一、判断直线和圆的位置关系
求圆心坐标及半径r（配方法）
圆心到直线的距离d （点到直线距离公式）
消去y（或x）
二、数学思想方法：
渗透了方程的思想和数形结合的思想．
判断方法笛卡尔之前的平面几何中就有，但要做到点到直线距离的精确计算，只有在笛卡尔、费马建立了解析几何才能做到。
这种方法在笛卡尔之前的平面几何中是没有的。只有笛卡尔和费马创立了解析结合才有了这种判断方法。
尊敬的邢启强老师（山东省滕州市第一中学）： 我在我自己制作的课件中采用了许多属于你的幻灯片。有人觉得我侵权，导致老师原创性制作课件的积极性大大降低。因为我，一些老师制作课件就不会再原创了，因为被剽窃却无法追责。对于导致老师原创课件积极性减弱的行为，我们要坚决反对，也要立规则保护老师的原创行为。因为有版权所以可以盈利导致经济纠纷这件事还是小事。 我是这么认为的。如果不直接使用你的幻灯片，那就要把你制作幻灯片的过程自己再制作一遍，于是就重复你的工作。我觉得这是何苦呢？何必呢？所以我义无反顾的采用了。并且我也把属于我自己的设计思想、理念、还有成果与你一起分享。你如果采用我的设计思想、理念和成果不用付费，我免费赠送。
此章此节该如何学习 穿越过去，到达笛卡尔时代，把自己当笛卡尔，把当时的数学知识重新发现一遍。你仿佛站在了人类文明的高山之巅，俯瞰大众，于是体会到了笛卡尔当年的高处不胜寒的滋味，也体会到笛卡尔当年一览众山小的感觉，更加体会到了创造是什么滋味。你开创了一个新时代，同学们。体会到了假如我是伟人是什么感觉。在数学学习中，人人都是伟人。 于是你会想假如我是笛卡尔，碰到当时的数学难题我改如何解答？请看下节直线与圆的方程的应用。
2.5.1直线与圆的位置关系
直线Ax＋By＋C＝0与圆(x－a)2＋(y－b)2＝r2的位置关系及判断
切线方程的求法1.求过圆上一点P(x0,y0)的圆的切线方程:先求切点与圆心连线的斜率k,则由垂直关系,切线斜率为- ,由点斜式方程可求得切线方程.若k=0或斜率不存在,则由图形可直接得切线方程为y=b或x=a.2.求过圆外一点P(x0,y0)的圆的切线时,常用几何方法求解设切线方程为y-y0=k(x-x0),即kx-y-kx0+y0=0,由圆心到直线的距离等于半径,可求得k,进而切线方程即可求出.但要注意,此时的切线有两条,若求出的k值只有一个时,则另一条切线的斜率一定不存在,可通过数形结合求出.
求直线与圆相交时弦长的两种方法(1)几何法:如图①,直线l与圆C交于A,B两点,设弦心距为d,圆的半
例1.如图是某圆拱形桥一孔圆拱的示意图.圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑，求支柱A2P2的高度（精确到0.01m).
分析：建立如图所示的直角坐标系，要得到支柱A2P2的高度，只需求出点P2的纵坐标.
解：建立如图所示的直角坐标系，使线段AB所在直线为x轴，O为坐标原点，圆心在y轴上，由题意，点P,B的坐标分别为（0,4),(10,0),设圆心坐标是(0,b),圆的半径是r，那么圆的方程是x2＋(y－b)2＝r2 .
思考:如果不建立平面直角坐标系，你能解决这个问题吗？由此比较综合法和坐标法的特点。
假如你是笛卡尔，你会如何看待此题？
我用自己创造出来的理论解决了这个数学难题。
几何法与解析法(坐标法）不同：几何法是每道题目解法都不同且技巧性很高难想到，而解析法（坐标法）是许多题目有相同的解题思路。几何法是个性非常强的方法，解析法（坐标法）是一般的、统一的、普遍的方法，易操作就是运算量比较大，但运算量比较大就交给计算机运算。
坐标法或解析法由后人发展出了平面几何的机器证明，中国代表人物是吴文俊。
某圆拱桥的水面跨度20m，拱高4m.现有一船，宽10m，水面以上高3m，这条船能否从桥下通过？
解　建立如图所示的坐标系.
依题意,有A(－10,0),B(10,0),P(0,4),D(－5,0)，E(5,0).设所求圆的方程是(x－a)2＋(y－b)2＝r2，
解此方程组，得a＝0，b＝－10.5，r＝14.5.
所以这座圆拱桥的拱圆的方程是x2＋(y＋10.5)2＝14.52(0≤y≤4).把点D的横坐标x＝－5代入上式，得y≈3.1.由于船在水面以上高3 m,3＜3.1，所以该船可以从桥下通过.
假如你是笛卡尔或费马，你解决了此题感觉如何？
答：内心涌现出巨大的成就感，这成就感让人感到狂喜不已，内心汹涌澎湃、翻江倒海。
例4一个小岛的周围有环岛暗礁，暗礁分布在以小岛中心为圆心，半径为20km的圆形区域内，已知小岛中心位于轮船正西40km处，港口位于小岛中心正北30km处.如果轮船沿直线返港，那么它是否会有触礁危险？
分析：先画出示意图,了解小岛中心、轮船、港口的方位和距离,如图,根据题意，建立适当的平面直角坐标系，求出暗礁所在区域的边缘圆的方程，以及轮船返港直线的方程，利用方程判断直线与圆的位置关系，进而确定轮船是否有触礁危险.
解：以小岛的中心为原点O,东西方向为x轴，建立如图所示的直角坐标系，为了运算的简便，我们取10km为单位长度，则港口所在位置的坐标为(0,3),轮船所在位置的坐标为(4,0).
由△=(-72)2-4×25×80