高中数学人教A版 (2019)选择性必修 第三册7.1 条件概率与全概率公式集体备课课件ppt

这是一份高中数学人教A版 (2019)选择性必修 第三册7.1 条件概率与全概率公式集体备课课件ppt，共31页。PPT课件主要包含了综合应用，全概率公式，加法公式，乘法公式，运用加法公式得到，另有一事件A则，巩固新知，根据题意得，由全概率公式得，可以理解为等内容，欢迎下载使用。
P(A+B)=P(A)+P(B)A、B互不相容
P(AB)=P(A)P(B|A)P(A)>0
看一个例子：有三个箱子，分别编号为1,2,3;1号箱装有1个红球4个白球，2号箱装有2红3白球，3号箱装有3个红球。某人从三个箱子中任取一箱，从中任意摸出一球，求取得红球的概率。
反思：我们把一个复杂事件B分解成几个简单的互斥事件的和，再运用条件概率的定义即乘法公式。所以不用死记硬背。
再对右边每一项运用乘法公式
将此列中所用的方法推广为一般得情形，就得到在概率计算中常用的全概率公式。
设随机试验的样本空间为Ω。
A＝AB1+AB2+……+ABn
B1,B2,…,Bn为互不相容的完备事件组(划分),且P(Bi)>0， i =1,2,…,n,
　　反思：我们把一个复杂事件B分解成几个简单的互斥事件的和，再运用条件概率的定义即乘法公式。所以不用死记硬背。
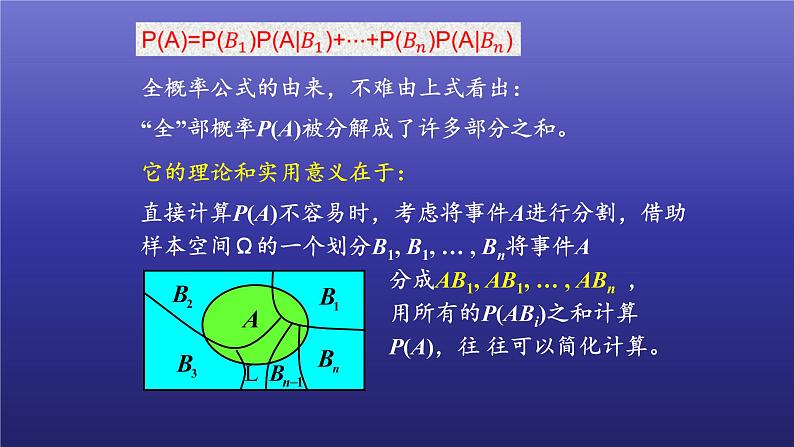
全概率公式的由来，不难由上式看出：
“全”部概率P(A)被分解成了许多部分之和。
它的理论和实用意义在于：
直接计算P(A)不容易时，考虑将事件A进行分割，借助样本空间Ω的一个划分B1, B1, … , Bn将事件A 分成AB1, AB1, … , ABn ， 用所有的P(ABi)之和计算 P(A)，往 往可以简化计算。
例4.某学校有A,B两家餐厅，王同学第1天午餐时随机地选择一家餐厅用餐。如果第1天去A餐厅，那么第二天去A餐厅的概率为0.6；如果第1天去B餐厅，那么第2天去A餐厅的概率是0.8.计算王同学第2天去A餐厅的概率。
因此，王同学第2天去A餐厅用餐得概率是0.7.
　　同学们，全概率公式对所有的概率概型都适用。但概率概型除了古典概型还有许多其它概型。比如几何概型、二项分布、超几何分布、正态分布等。所以每个概型都有自己的一种解法。此题是古典概型，所以有非常简单的解法。
设B=“任取一个零件为次品”，
设随机试验是样本空间为Ω。
B1,B2,…,Bn为互不相容的完备事件组(划分), 且P(Bi)>0， i =1,2,…,n,
注：贝叶斯公式需要死记硬背吗？
答：左边=中间是条件概率定义。中间=右边是中间式子的分子再一次用条件概率定义。然后，中间式子分母用全概率公式代入。死记硬背也记不住。
贝叶斯公式在实际中有很多应用，它可以帮助人们确定某结果(事件A)发生的最可能的原因。
该公式由贝叶斯(Bayes)给出。他是在观察到事件A已发生的条件下，寻找导致A发生的每个原因的概率。贝叶斯公式的思想就是“执果溯因”。全概率公式的思想是“由因推果”。
例6.在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干扰,发送的信号0或1有可能被错误地接收 为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;已知发送信号1时,接收为1和0的概率分别为0.95和0.05.假设发送信号0和1是等可能的.
(1)分别求接收为0和1的概率;
设A=“发送的信号为0”，B=“接收到的信号为0”
P(A)=P(B)=0.5,P(B|A)=0.9
同学们，全概率公式对所有的概率概型都适用。但概率概型除了古典概型还有许多其它概型。比如几何概型、二项分布、超几何分布、正态分布等。所以每个概型都有自己的一种解法。此题是古典概型，所以有非常简单的解法。
例6.在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干扰,发送的信号0或1有可能被错误地接收 为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;已知发送信号1时,接收为1和0的概率分别为0.95和0.05.假设发送信号0和1是等可能的.
*(2)已知接收的信号为0,求发送的信号是1的概率.
例6.在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干扰,发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;已知发送信号1时,接收为1和0的概率分别为0.95和0.05.假设发送信号0和1是等可能的.
　　同学们，贝叶斯公式对所有的概率概型都适用。但概率概型除了古典概型还有许多其它概型。比如几何概型、二项分布、超几何分布、正态分布等。所以每个概型都有自己的一种解法。此题是古典概型，所以有非常简单的解法。
5.例6.在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干扰,发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;已知发送信号1时,接收为1和0的概率分别为0.95和0.05.假设发送信号0和1是等可能的.
因为发送信号0和1是等可能的。所以假设有100个0和100个1发送。100个0发送，接收为0的有90个，接收为1的有10个。100个1发送，接收为0的有5个，接收为1的有95个。所以总共接收的0有90+5=95，总共接收的1有10+95=105
例 3 (疾病普查问题)某一地区患有癌症的人占0.005，患者对一种试验反应是阳性的概率为0.95，正常人对这种试验反应是阳性的概率为0.04，现抽查了一个人，试验结果是阳性，问此人是癌症患者的概率有多大?
设 A ＝{试验结果是阳性}，
B1＝{抽查的人患有癌症}
B2＝{抽查的人不患有癌症}
P(B1)=0.005
P(B2)=0.995
P(A|B1)=0.95
P(A|B2)=0.04
现在来分析一下结果的意义：
2. 检出阳性是否一定患有癌症?
1. 这种试验对于诊断一个人是否患有癌症有无意义？
如果不做试验，抽查一人，他是患者的概率 P(C)=0.005
患者阳性反应的概率是0.95，若试验后得阳性反应，则根据试验得来的信息，此人是患者的概率为 P(C｜A)= 0.1066
说明这种试验对于诊断一个人是否患有癌症有意义。
从0.005增加到0.1066,将近增加约21倍。
试验结果为阳性,此人确患癌症的概率为 P(C｜A)=0.1066
即使你检出阳性，尚可不必过早下结论你有癌症，这种可能性只有10.66% (平均来说，1000个人中大约只有107人确患癌症)，此时医生常要通过再试验来确认.
P(Bi)(i=1,2,…,n)是在没有进一步信息（不知道事件A是否发生）的情况下，人们对诸事件发生可能性大小的认识。
当有了新的信息（知道A发生），人们对诸事件发生可能性大小P(Bi | A)有了新的估计。
贝叶斯公式从数量上刻划了这种变化。
它们是加法公式和乘法公式的综合运用，同学们可通过进一步的练习去掌握它们。
1) 全概率公式主要用在事件A的发生有各种可能的原因Bi，这里B1, B2, … , Bn互斥。
第一种原因B1可能导致事件A发生，即：AB1第二种原因B2可能导致事件A发生，即：AB2……第n种原因Bn可能导致事件A发生，即：ABn则事件A发生的概率就可以由全概率公式计算。
2) 贝叶斯公式主要用在事件A已发生的情况下，考虑各种可能的原因Bi，