2022届中考数学二轮专题复习-矩形、菱形及正方形解析版

这是一份2022届中考数学二轮专题复习-矩形、菱形及正方形解析版，共49页。试卷主要包含了单选题，填空题，计算题，解答题，综合题等内容，欢迎下载使用。
 中考数学二轮专题复习-矩形、菱形及正方形
一、单选题
1．下列四边形中，对角线互相垂直平分的是（　　）
A．平行四边形、菱形 B．矩形、菱形
C．矩形、正方形 D．菱形、正方形
2．下列测量方案中，能确定四边形门框为矩形的是（　　）
A．测量对角线是否互相平分
B．测量两组对边是否分别相等
C．测量对角线是否相等
D．测量对角线交点到四个顶点的距离是否都相等
3．如图，菱形 的对角线 、 相交于点 ，过点 作 于点 ，连接 ，若 ， ，则菱形 的面积为（　　）

A． B． C． D．
4．如图，有甲、乙、丙三个矩形，其中相似的是（　　）

A．甲与丙 B．甲与乙
C．乙与丙 D．三个矩形都不相似
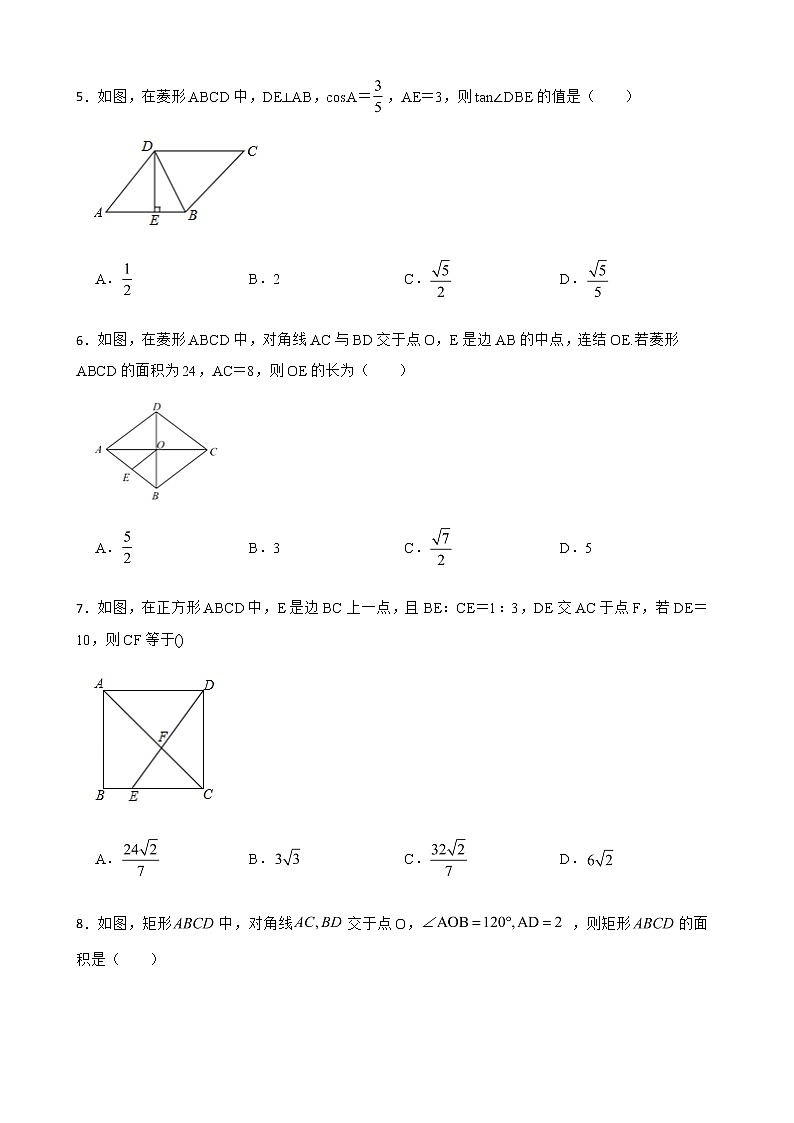
5．如图，在菱形ABCD中，DE⊥AB，cosA＝，AE＝3，则tan∠DBE的值是（　　）

A． B．2 C． D．
6．如图，在菱形ABCD中，对角线AC与BD交于点O，E是边AB的中点，连结OE.若菱形ABCD的面积为24，AC＝8，则OE的长为（　　）

A． B．3 C． D．5
7．如图，在正方形ABCD中，E是边BC上一点，且BE：CE＝1：3，DE交AC于点F，若DE＝10，则CF等于()

A． B． C． D．
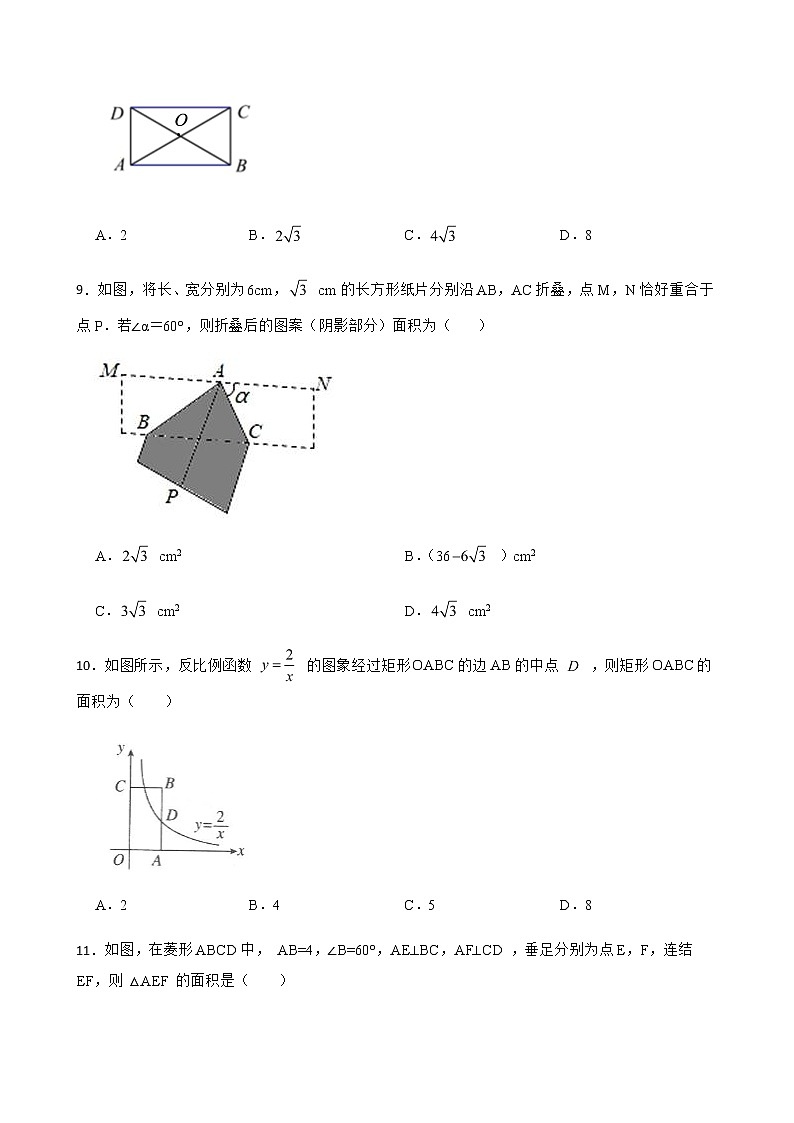
8．如图，矩形中，对角线交于点O，，则矩形的面积是（　　）

A．2 B． C． D．8
9．如图，将长、宽分别为6cm， cm的长方形纸片分别沿AB，AC折叠，点M，N恰好重合于点P．若∠α＝60°，则折叠后的图案（阴影部分）面积为（　　）

A． cm2 B．（36 ）cm2
C． cm2 D． cm2
10．如图所示，反比例函数 的图象经过矩形OABC的边AB的中点 ，则矩形OABC的面积为（　　）

A．2 B．4 C．5 D．8
11．如图，在菱形ABCD中， AB=4，∠B=60°，AE⊥BC，AF⊥CD ，垂足分别为点E，F，连结EF，则 △AEF 的面积是（　　）

A． B． C． D．
12．如图，四边形ABCD是正方形，BE⊥EF，DF⊥EF，BE=2.5dm，DF=4dm，那么EF的长为（　　）

A．6.5dm B．6dm C．5.5dm D．4dm
13．将一矩形纸片ABCD沿CE折叠，B点恰好落在AD边上的F处，若 ，则 的值为（　　）

A． B． C． D．
14．正方形ABCD的边长为8，M在DC上，且DM＝2，N是AC上的一动点，DN＋MN的最小值为（　　）

A．6 B．8 C．10 D．9
15．如图，在矩形ABCD中，对角线、BD交于C，，垂足为E，，那么的面积是（　　）

A． B． C． D．
16．如图，在Rt△ABC中，∠ACB＝90°，以其三边为边向外作正方形，过点C作CI⊥HJ于点I，交AB于K，在图形的外部作矩形MNPQ，使点D，E，G和H，J都落在矩形的边上.已知矩形BJIK的面积为1，正方形ACDE的面积为4，则 为（　　）

A． B． C． D．
17．如图，正方形 的边长为a，点E在边 上运动（不与点A，B重合）， ，点F在射线 上，且 与 相交于点G，连接 ．则下列结论：① ，② 的周长为 ，③ ；④当 时，G是线段 的中点，其中正确的结论是（　　）

A．①②③ B．①④ C．①③④ D．①②③④
18．如图，菱形ABCD的边长为4，E、F分别是AB、AD上的点，AC与EF相交于点G，若 ， ，则FG的长为（　　）

A． B．2 C．3 D．4
19．如图，在△ABC中，∠ACB＝90°，以△ABC的各边为边分别作正方形BAHI，正方形BCFG与正方形CADE，延长BG，FG分别交AD，DE于点K，J，连结DH，IJ.图中两块阴影部分面积分别记为S1，S2.若S1：S2＝1：4，S四边形边BAHE＝18，则四边形MBNJ的面积为（　　）

A．5 B．6 C．8 D．9
20．如图，在Rt△ABC中，∠CBA＝60°，斜边AB＝10，分别以△ABC的三边长为边在AB上方作正方形，S1，S2，S3，S4，S5分别表示对应阴影部分的面积，则S1+S2+S3+S4+S5＝（　　）

A．50 B．50 C．100 D．100
二、填空题
21．在四边形ABCD中，对角线AC，BD交于点O，OA=OC=OB=OD，添加一个条件使四边形ABCD是正方形，那么所添加的条件可以是　 　(写出一个即可)
22．如图， 分别以Rt△ABC三边构造三个正方形，面积分别为S1，S2，S3，若S1=15，S3=39，则S2=　 　.

23．如图，在平面直角坐标系中，点A1（1，0）、A2（3，0）、A3（6，0）、A4（10，0）、……，以A1A2为对角线作第一个正方形A1C1A2B1，以A2A3为对角线作第二个正方形A2C2A3B2，以A3A4，为对角线作第三个正方形A3C3A4B3，……，顶点B1，B2，B3……都在第一象限，按照此规律依次下去，则点Bn的坐标为　 　.

24．如图，菱形ABCD的对角线 ，BD相交于点 ， ， ，以AB为直径作一个半圆，则图中阴影部分的面积为　 　.

25．如图，在矩形ABCD中，AB＝8，AD＝10，AD，AB，BC分别与⊙O相切于E，F，G三点，过D作⊙O的切线交BC于点M，切点为N，则DM的长为 　 　.

26．建党100周年主题活动中，702班浔浔设计了如图1的“红色徽章”其设计原理是：如图2，在边长为的正方形四周分别放置四个边长为的小正方形，构造了一个大正方形，并画出阴影部分图形，形成了“红色徽章”的图标.现将阴影部分图形面积记作，每一个边长为的小正方形面积记作，若，则的值是　 　.

27．如图，正方形ABCD的边长为4，P是边CD上的一动点，EF⊥BP交BP于G，且EF平分正方形ABCD的面积，则线段GC的最小值是　 　.

28．正方形ABCD的边长为4，点E是BC边上的一动点，连结AE，过点B作BF⊥AE于点F，以BF为边作正方形FBHG，当点E从B运动到C时，求CF的最短距离为　 　；线段HG扫过的面积为　 　

29．如图，在矩形ABCD中，AB＝4，BC＝3，将△BCD沿射线BD平移长度a（a＞0）得到△B'C'D'，连接AB'，AD'，则当△AB'D'是直角三角形时，a的长为　 　.

30．如图，矩形ABCD中，AB＝20，AD＝15，P，Q分别是AB，AD边上的动点，PQ＝16，以PQ为直径的⊙O与BD交于点M，N，则MN的最大值为　 　．

三、计算题
31．如图，在中，，D为的中点，，，连接交于点O.

（1）证明：四边形为菱形；
（2）若，，求菱形的高.
32．如图，已知在矩形ABCD中，AB=6，BC=2，点E，F分别在边CD，AB上，且DE=BF.

（1）求证:四边形AFCE是平行四边形；
（2）若□AFCE是菱形，求菱形AFCE的边长.
四、解答题
33．如图，在四边形ABCD中，E，F，G，H分别是AB，BD，CD，AC的中点，AD＝BC，求证：四边形EFGH是菱形．

34．如图，矩形ABCD中，BC=4，将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D′，此时点B′恰好落在边AD上．连接B′B，若∠AB′B=75°，求旋转角及AB长．

35．如图，△ABC中，点D是边AC的中点，过D作直线PQ∥BC，∠BCA的平分线交直线PQ于点E，点G是△ABC的边BC延长线上的点，∠ACG的平分线交直线PQ于点F．求证：四边形AECF是矩形．

36．在几何探究问题中，经常需要通过作辅助线（如，连接两点，过某点作垂线，作延长线，作平行线等等）把分散的条件相对集中，以达到解决问题的目的.

（1）（探究发现）如图1，点E，F分别在正方形ABCD的边BC，CD上， ，连接EF.通过探究，可发现BE，EF，DF之间的数量关系为　 　（直接写出结果）.
（2）（验证猜想）同学们讨论得出下列三种证明思路（如图1）：
思路一：过点A作 ，交CD的延长线于点G.
思路二：过点A作 ，并截取 ，连接DG.
思路三：延长CD至点G，使 ，连接AG.
请选择你喜欢的一种思路证明（探究发现）中的结论.
（3）（迁移应用）如图2，点E，F分别在正方形ABCD的边BC，CD上，且 ， ，设 ，试用含 的代数式表示DF的长.
37．在平面直角坐标系中，O为原点，点A（6，0），点B在y轴的正半轴上，∠ABO＝30°．矩形CODE的顶点D，E，C分别在OA，AB，OB上，OD＝2．

（Ⅰ）如图①，求点E的坐标；
（Ⅱ）将矩形CODE沿x轴向右平移，得到矩形C′O′D′E′，点C，O，D，E的对应点分别为C′，O′，D′，E′．设OO′＝t，矩形C′O′D′E′与△ABO重叠部分的面积为S．
①如图②，当矩形C′O′D′E′与△ABO重叠部分为五边形时，C′E′，E′D′分别与AB相交于点M，F，试用含有t的式子表示S，并直接写出t的取值范围；
②当 ≤S≤5 时，求t的取值范围（直接写出结果即可）．
38．阅读下面的例题及点拨，并解决问题：
例题：如图①，在等边 中， 是 边上一点(不含端点 )， 是 的外角 的平分线上一点，且 .求证： .
点拨：如图②，作 ， 与 的延长线相交于点 ，得等边 ，连接 .易证： ，可得 ；又 ，则 ，可得 ；由 ，进一步可得 又因为 ，所以 ，即： .
问题：如图③，在正方形 中， 是 边上一点(不含端点 )， 是正方形 的外角 的平分线上一点，且 .求证： .


五、综合题
39．将 绕点A按逆时针方向旋转 度，并使各边长变为原来的n倍，得 ，如图①，我们将这种变换记为 .

（1）如图①，对 作变换 得 ，则 　 　；直线 与直线 所夹的锐角为　 　度；
（2）如图②， 中， ，对 作变换 得 ，使点B、C、 在同一直线上，且四边形 为矩形，求 和n的值；
（3）如图③， 中， ，对 作变换 得 ，使点B、C、 在同一直线上，且四边形 为平行四边形，求 和n的值.
40．如图

（1）如图1，正方形ABCD与调研直角△AEF有公共顶点A，∠EAF＝90°，连接BE、DF，将△AEF绕点A旋转，在旋转过程中，直线BE、DF相交所成的角为β，则＝　 　；β＝　 　；
（2）如图2，矩形ABCD与Rt△AEF有公共顶点A，∠EAF＝90°，且AD＝2AB，AF＝2AE，连接BE、DF，将Rt△AEF绕点A旋转，在旋转过程中，直线BE、DF相交所成的角为β，请求出的值及β的度数，并结合图2进行说明；
（3）若平行四边形ABCD与△AEF有公共项点A，且∠BAD＝∠EAF＝α(0°＜α＜180°)，AD＝kAB， AF＝kAE(k≠0)，将△AEF绕点A旋转，在旋转过程中，直线BE、DF相交所成的锐角的度数为β，则：
①＝　 　；
②请直接写出α和β之间的关系式　 　．

答案解析部分
【解析】【解答】解：∵平行四边形对角线互相平分，菱形对角线互相垂直平分，
矩形对角线互相平分且相等，正方形对角线互相垂直平分且相等，
∴A、B、C不符合题意，D符合题意.
故答案为：D.
【分析】根据平行四边形对角线互相平分，菱形对角线互相垂直平分，矩形对角线互相平分且相等，正方形对角线互相垂直平分且相等，即可得出答案.
【解析】【解答】解：A、∵对角线互相平分的四边形是平行四边形，而对角线互相平分且相等的四边形才是矩形，
∴选项A不符合题意；
B、∵两组对边分别相等是平行四边形，
∴选项B不符合题意；
C、∵对角线互相平分且相等的四边形才是矩形，
∴对角线相等的四边形不是矩形，
∴选项C不符合题意；
D、∵对角线交点到四个顶点的距离都相等，
∴对角线互相平分且相等，
∵对角线互相平分且相等的四边形是矩形，
∴选项D符合题意.
故答案为：D.
【分析】利用对角线互相平分且相等的四边形是矩形，可作出判断.
【解析】【解答】解：∵四边形ABCD是菱形，
∴OA=OC，OB=OD，AC⊥BD，
∵DH⊥AB，
∴∠BHD=90°，
∴BD=2OH，
∵OH=2，
∴BD=4，
∵OA=3，
∴AC=6，
∴菱形ABCD的面积 ．
故答案为：A．

【分析】根据菱形的性质和直角三角形斜边上的中线定理求出对角线的长即可求出菱形的面积。
【解析】【解答】解：三个矩形的角都是直角，甲、乙、丙相邻两边的比分别为4：6＝2：3，1.5：2＝3：4，2：3，
∴甲和丙相似.
故答案为：A.
【分析】分别求出甲、乙、丙相邻两边的比，然后结合相似图形的概念进行判断.
【解析】【解答】解：∵DE⊥AB，cosA＝，AE＝3，
∴，解得：AD＝5.
∴DE＝ ＝4，
∵四边形ABCD是菱形，∴AD=AB=5，
∴BE＝5﹣3＝2，
∴tan∠DBE＝ ＝2.
故答案为：B.
【分析】根据余弦函数的概念可得AD的值，利用勾股定理求出DE，根据菱形的性质可得AD=AB=5，然后求出BE的值，再根据正切函数的概念进行计算.
【解析】【解答】解：由题意知 ，AC⊥BD
∴
∴
在 中，由勾股定理得
∵点E为AB中点
∴OE是△ABD的中位线
∴ .
故答案为：A.
【分析】根据菱形的面积以及菱形的性质可得BD=6，则OA=4，OD=3，利用勾股定理求出AD，易得OE是△ABD的中位线，据此解答.
【解析】【解答】解：∵四边形ABCD为正方形，
∴BC＝DC
∵BE：CE＝1：3，
∴EC：BC＝3：4
∵DE＝10
∴设EC＝3x，则BC＝4x
在Rt△DCE中，有100＝(3x)2+(4x)2，解得x＝2
则EC＝6，DC＝8
同理得，AC＝8
∵易证△FEC∽△FDA
∴ ，
∴FA＝ FC
∵AC＝AF+FC
∴8 ＝FC+ FC，
得FC＝
故答案为：A.
【分析】根据正方形的性质可得BC＝DC，结合已知条件可设EC＝3x，则BC＝4x，在Rt△DCE中，由勾股定理可得x，进而可得EC、CD、AC，易证△FEC∽△FDA，根据相似三角形的性质表示出FA，然后根据AC＝AF+FC就可求出FC.
【解析】【解答】解：∵四边形ABCD是矩形，
，
，
∴，
△AOD是等边三角形，
，
在Rt△ADB中，，
∴

矩形ABCD的面积是
故答案为：C.
【分析】根据矩形的性质可得OA=OB=OD，∠DAB=90°，根据邻补角的性质可得∠AOD=60°，推出△AOD是等边三角形，得到∠ADB=60°，则∠ABD=30°，根据含30°角的直角三角形的性质可得BD=2AD=4，利用勾股定理求出AB，然后根据矩形的面积公式进行计算.
【解析】【解答】解：根据翻折可得，∠MAB=∠PAB，∠NAC=∠PAC
∴∠BAC=∠PAB+∠PAC=（∠MAB+∠PAB+∠NAC+∠PAC）=×180°=90°
∵∠α＝60°
∴∠MAB=180°-∠BAC-∠α=180°-90°-60° =30°
∵长方形的长、宽分别为6cm、 cm
∴AB=，AC=
​​​​​​​∴阴影部分的面积=
​​​​​​​故答案为：D.
【分析】根据翻折的性质可以得出∠BAC=90°以及∠MAB=30°，结合角度，运用解直角三角形，可以计算出AB、AC的长，再根据阴影部分的面积=长方形面积-三角形ABC的面积，代入数值，可以算出阴影部分的面积，从而得到答案.
【解析】【解答】解：如图，过点D作DE⊥OC于点E，

∵反比例函数y=的图象经过矩形OABC的边AB的中点D，
∴S矩形OABC=2S矩形OADE，
又∵k=2，
∴S矩形OADE=2，
∴S矩形OABC=4.
故答案为：B.
【分析】过点D作DE⊥OC于点E，由反比例函数的图象经过矩形OABC的边AB的中点D，可得S矩形OABC=2S矩形OADE，再利用k的几何意义可得S矩形OADE=2，即可求解.
【解析】【解答】解：如图，过点A作AH⊥EF于点H，

∵菱形ABCD，
∴BC=CD，∠B=∠D=60°，
∴∠BAD=180°-60°=120°，
∵AE⊥BC，AF⊥CD，
∴∠AEB=∠AFD=90°，
∴∠BAE=∠DAF=30°，
∴∠EAF=∠BAD-∠BAE-∠DAF=120°-30°-30°=60°，
又∵BC·AE=CD·AF，
∴AE=AF，
∴△AEF为等边三角形，
∴AE=EF=AF，EH=HF=EF，AH=EH，
∵AB=4，
∴在Rt△AEB中，BE=AB=2，
∴EF=AF=AE=BE=2，
∴AH=EH=3，
∴S△AEF=EF·AH=×2×3=3.
故答案为：B.
【分析】如图，过点A作AH⊥EF于点H，根据菱形性质得，BC=CD，∠B=∠D=60°，再求得∠BAD，由AE⊥BC，AF⊥CD，得∠AEB=∠AFD=90°，进而求出∠BAE=∠DAF=30°，可求得∠EAF=60°，根据菱形面积相等得BC·AE=CD·AF，即AE=AF，证明出△AEF为等边三角形，进而得到AE=EF=AF，EH=HF=EF，AH=EH，再在Rt△AEB中，求得BE，即可求出AH，最后通过三角形面积公式计算即可解决问题.
【解析】【解答】解：∵四边形ABCD是正方形，
∴BC=CD，BC⊥CD，
∴∠BCE+∠FCD=90°，
又∵BE⊥EF，DF⊥EF，
∴∠BEC=∠CFD=90°，
∴∠BCE+∠EBC=90°，
∴∠EBC=∠FCD，
∴△BEC≌△CFD，
∴BE=CF=2.5dm，DF=EC=4dm，
∴EF=EC+CF=6.5dm.
故答案为：A.
【分析】根据正方形性质得，BC=CD，BC⊥CD，根据同角的余角相等得∠EBC=∠FCD，利用AAS可证明△BEC≌△CFD，根据全等三角形性质可得BE=CF=2.5dm，DF=EC=4dm，再由EF=EC+CF即可求解.
【解析】【解答】解：∵∠AFE＋∠CFD＝90°，
∴ ，
由折叠可知，CB＝CF，
矩形ABCD中，AB＝CD， .
故答案为：D.
【分析】根据互余两角三角函数的关系可得cos∠AFE=sin∠CFD，由折叠的性质可得CB=CF，由矩形的性质可得AB=CD，然后利用三角函数的概念进行计算.
【解析】【解答】根据题意，连接BN，BM，


三点共线时，DN＋MN取得最小值，
则BM就是DN＋MN的最小值，
在Rt△BCM中，BC=8，CM=6，
根据勾股定理得：，
即DN＋MN的最小值是10，
故答案为：C

【分析】连接BN，BM，当B、M、N三点共线时，DN＋MN取得最小值，再利用勾股定理求出BM的长即可。
【解析】【解答】解：如图：过点C作CF⊥BD于F．

∵矩形ABCD中，BC＝2，AE⊥BD，
∴∠ABE＝∠CDF＝60°，AB＝CD，AD＝BC＝2，∠AEB＝∠CFD＝90°．
∴△ABE≌△CDF，（AAS），
∴AE＝CF．
∵∠ABE＝∠CDF＝60°，
∴∠ADE＝∠CBF＝30°，
∴CF＝AE＝AD＝1，
∴BE＝ =AE＝，
∵∠ABE＝60°，AO=BO，
∴△ABO是等边三角形，
∴OE＝BE=，
∴S△ECO＝OE•CF＝，
故答案为：B．

【分析】过点C作CF⊥BD于F．根据矩形的性质得出∠ABE＝∠CDF＝60°，AB＝CD，AD＝BC＝2，∠AEB＝∠CFD＝90°．根据全等三角形的性质得出AE＝CF．解直角三角形得出OE的值，根据三角形面积公式即可得出结论。
【解析】【解答】解：如图，延长AB交PN于点R，延长BA交MQ于点L，连结AG、CJ，设BK＝m，

∵四边形BCFG和四边形ABJH都是正方形，四边形BJIK是矩形，
∴BG＝BC，BA＝BJ，∠CBG＝∠ABJ＝90°
∴∠ABG＝∠JBC＝90°+∠ABC，
∴△ABG≌△JBC（SAS），
∴S△ABG＝S△JBC，
∵S△ABG＝ BG•BC＝ S正方形BCFG，S△JBC＝ BJ•BK＝ S矩形BJIK，
∴ S正方形BCFG＝ S矩形BJIK，
∴BC2＝S正方形BCFG＝S矩形BJIK＝1，
∴BC＝1，
∵四边形ACDE是正方形，且AC2＝S正方形ACDE＝4，
∴AC＝2，
∵CI⊥HJ于点I，交AB于K，AB∥HJ，
∴∠CKB＝∠CIJ＝90°，
∵∠ACB＝90°，
∴∠CKB＝∠ACB，
∵∠CBK＝∠ABC，
∴△CBK∽△ABC，
∴ ，
∴ ＝ ，
∴CK＝2BK＝2m，
∵∠AKC＝∠ACB＝90°，∠CAK＝∠BAC，
∴△ACK∽△ABC，
∴ ，
∴ ＝ ，
∴AK＝2CK＝4m，
∵四边形MNPQ和四边形BJIK都是矩形，
∴∠M＝∠N＝∠P＝∠Q＝∠PRL＝90°，
∴∠LRN＝90°，
∴四边形MNRL和四边形PQLR都是矩形，
∴∠ALQ＝90°，
∵∠AHJ＝90°，
∴∠AHQ＝90°，
∴四边形AHQL是矩形，
∴QL＝AH＝AB＝m+4m＝5m，
∵∠M＝∠ELA＝∠AKC＝∠AED＝∠CAE＝90°，
∴∠MED＝90°﹣∠AEL＝∠LAE＝90°﹣∠CAK＝∠KCA，
∵DE＝EA＝AC，
∴△DEM≌△EAL≌△ACK（AAS），
∵EM＝AL＝CK＝2m，EL＝AK＝4m，
∴MQ＝2m+4m+5m＝11m，
∵∠BRG＝∠CKB＝∠CBG＝90°，
∴∠BGR＝90°﹣∠GBR＝∠CBK，
∵BG＝BC，
∴△BGR≌△CBK（AAS），
∴BR＝CK＝2m，
∴MN＝LR＝2m+5m+2m＝9m，
∴ ，
故答案为：D.

【分析】延长AB交PN于点R，延长BA交MQ于点L，连结AG、CJ，设BK＝m，先根据“SAS”定理证明△ABG≌△JBC，推出BC2＝S正方形BCFG＝S矩形BJIK＝1，得BC＝1，再由四边形ACDE是正方形，且AC2＝S正方形ACDE＝4，得AC＝2；再通过相似三角形判定定理证明△CBK∽△ABC，△ACK∽△ABC，由相似三角形对应比成比例推出CK=2BK=2m，AK=2CK=4m；再证明出四边形MNRL、四边形PQJR和四边形AHQJ都为矩形，则QL＝AH＝=AB=5m；再根据“AAS”定理证明△DEM≌△EAL≌△ACK，可得EM=AL=CK=2m，EL=AK=4m，可求得MQ=11m；再由“AAS”定理证明△BGR≌△CBK，可得BR=CK=2m，可求得MN=9m，可求得，即可解决问题.
【解析】【解答】解：①如图1，在BC上截取BH=BE，连接EH

∵BH=BE，∠EBH=90°
∴EH=BE
∵AF=BE
∴AF=EH
∵∠DAM=∠EHB=45°，∠BAD=90°
∴∠FAE=∠EHC=135°
∵BA=BC，BE=BH
∴AH=HC
∴
∴EF=EC，∠AEF=∠ECB
∵∠ECH+∠CEB=90°
​​​​​​​∴∠AEF+∠CEB=90°
∴∠CEF=90°
∴∠ECF=∠EFC=45°，故①正确；
②、③如图2，延长AD到H，使DH=BE，则

∴∠ECB=∠DCH
∴∠ECH=∠BCD=90°
∴∠ECG=∠GCH=45°
∵CG=CG，CE=CH
∴
∴EG=GH
∵GH=DG+DH，DH=BE
​​​​​​​∴EG=BE+DG，故③错误；
∵ △AEG的周长=AE+EG+AG=AE+AH=AD+DH+AE=AE+EB+AD=AB+AD=2a
​​​​​​​∴②错误；
④∵当 时 ，设DG=x
​​​​​​​∴EG=
∵在Rt中，EG2=AG2+AE2
​​​​​​​∴
解得x= a
∴AG=GD，即G是线段AD的中点，故④正确
综上所述，正确的有①④.
故答案为：B.
【分析】①如图1，在BC上截取BH=BE，连接EH，之后证明△FAE≌△EHC即可求解；
②③如图2，延长AD到H，使DH=BE，则△CBE≌△CDH ，之后再证明△GCE≌△GCH即可求解；
④当 时 ，设DG=x，则​​EG= ，之后运用勾股定理EG2=AG2+AE2建立等式解出x，即可求解.
【解析】【解答】解：过点E作EM∥BC交AC于M，EN⊥BC于N，如图所示：

∵菱形ABCD的边长为4，∠BAD＝120°，
∴AB＝BC＝4，∠BAC＝∠FAC＝ ∠BAD＝60°，AD∥BC，
∴△ABC是等边三角形，
∴∠B＝∠ACB＝60°，BC＝AC，
∵EM∥BC，
∴EM∥AD，∠AEM＝∠B＝60°＝∠BAC，
∴△AEM是等边三角形，
∴AM＝AE＝AB﹣BE＝4﹣1＝3，
∵EM∥AD，
∴△AGF∽△MGE，
∴ ＝ ＝ ，
∴FG＝ EF，
在△BCE和△ACF中，
，
∴△BCE≌△ACF（SAS），
∴CE＝CF，∠BCE＝∠ACF，
∴∠ACF+∠ACE＝∠ACF+∠ACE＝∠ACB＝60°，
∴△CEF是等边三角形，
∴EF＝CE，
∵EN⊥BC，∠B＝60°，
∴∠BEN＝30°，
∴BN＝ BE＝ ，
∴EN＝ BN＝ ，CN＝BC﹣BN＝4﹣ ＝ ，
∴EF＝CE＝ ＝ ＝ ，
∴FG＝ EF＝ .
故答案为：A.
【分析】过点E作EM∥BC交AC于M，EN⊥BC于N，根据菱形的性质可得AB＝BC＝4，∠BAC＝∠FAC＝60°，AD∥BC，推出△ABC、△AEM是等边三角形，证明△AGF∽△MGE，根据相似三角形的性质可得FG＝ EF，然后证明△BCE≌△ACF，得到CE＝CF，∠BCE＝∠ACF，推出△CEF是等边三角形，则EF＝CE，易得∠BEN＝30°，根据含30°角的直角三角形的性质可得BN，由三角函数的性质求出EN，进而求出CN，由勾股定理可得EF，然后根据FG＝EF就可得到FG的长.
【解析】【解答】解：∵四边形BAHI和四边形CADE都是正方形，
∴AC＝AD，AB＝AH，∠CAD＝∠ABI＝∠BAH＝∠ADE＝90°，
∴∠CAB+∠BAD＝∠DAH+∠BAD，
∴∠CAB＝∠DAH，
在△CAB和△DAH中，
，
∴△CAB≌△DAH（SAS），
∴∠ADH＝∠ACB＝90°，
∵∠ADE＝90°，
∴H、D、E三点共线，
∵四边形BCFG和四边形CADE都是正方形，延长BG、FG分别交AD、DE于点K、J，
∴四边形ADJF和四边形BEDK都是矩形，且AF＝BE，∠AFN＝∠BEM＝90°，四边形DKGJ是正方形，四边形CFJE是矩形，
∵S1：S2＝1：4，
∴
∴BC＝FC＝FG＝BG＝2GJ，
∵四边形CADE是正方形，
∴∠ADE＝90°，AC＝AD＝DE＝CE＝BC+GJ＝3GJ，
在Rt△ACB中，由勾股定理得： ，
在Rt△ADH中，由勾股定理得：
∵S四边形BAHE＝S△ADH+S梯形ADEB＝18，
∴ AD•DH+ （AD+BE）•DE＝ ×3GJ×2GJ+ （3GJ+GJ）×3GJ＝18，
解得：GJ＝ （负值已舍去），
∵∠ABC+∠EBM＝180°﹣∠ABI＝180°﹣90°＝90°，∠ABC+∠CAB＝90°，
∴∠CAB＝∠EBM，即∠FAN＝∠EBM，
在△FAN和△EBM中，
，
∴△FAN≌△EBM（ASA），
∴S△FAN＝S△EBM，
∴S△ABC＝S四边形BCFN+S△FAN＝S四边形BCFN+S△EBM，
∴S四边形MBNJ＝S矩形CFJE﹣S四边形BCFN﹣S△EBM＝S矩形CFJE﹣S△ABC＝FC•CE﹣ AC•BC＝2GJ×3GJ﹣ ×3GJ×2GJ＝3GJ2＝3×（ ）2＝6.
故答案为：B.
【分析】根据正方形的性质可得AC＝AD，AB＝AH，∠CAD＝∠ABI＝∠BAH＝∠ADE＝90°，推出∠CAB＝∠DAH，证明△CAB≌△DAH，推出H、D、E三点共线，延长BG、FG分别交AD、DE于点K、J，根据矩形的性质可得AF＝BE，∠AFN＝∠BEM＝90°，由S1:S2＝1:4可得BC＝FC＝FG＝BG＝2GJ，根据勾股定理表示出AB、DH，然后根据S四边形BAHE＝S△ADH+S梯形ADEB＝18结合三角形、梯形的面积公式可求出GJ，证明△FAN≌△EBM，得到S△FAN＝S△EBM，则S四边形MBNJ＝S矩形CFJE-S四边形BCFN-S△EBM＝S矩形CFJE-S△ABC，据此计算.
【解析】【解答】解：在Rt△ABC中，∠CBA＝60°，斜边AB＝10，
∴BC＝AB＝5，AC＝＝5，
过D作DN⊥BF于N，连接DI，

在△ACB和△BND中，
，
∴△ACB≌△BND（AAS），
同理，Rt△MND≌Rt△OCB，
∴MD＝OB，∠DMN＝∠BOC，
∴EM＝DO，
∴DN＝BC＝CI，
∵DN∥CI，
∴四边形DNCI是平行四边形，
∵∠NCI＝90°，
∴四边形DNCI是矩形，
∴∠DIC＝90°，
∴D、I、H三点共线，

∵∠F＝∠DIO＝90°，∠EMF＝∠DMN＝∠BOC＝∠DOI，
∴△FME≌△DOI（AAS），
∵图中S2＝SRt△DOI，S△BOC＝S△MND，
∴S2+S4＝SRt△ABC，S3＝S△ABC，
在Rt△AGE和Rt△ABC中，
，
∴Rt△AGE≌Rt△ACB（HL），
同理，Rt△DNB≌Rt△BHD，
∴S1+S2+S3+S4+S5
＝S1+S3+（S2+S4）+S5
＝Rt△ABC的面积+Rt△ABC的面积+Rt△ABC的面积+Rt△ABC的面积
＝Rt△ABC的面积×4
＝5×5÷2×4
＝50.
故答案为：B.
【分析】过D作DN⊥BF于N，连接DI，证明△ACB≌△BND，Rt△MND≌Rt△OCB，△FME≌△DOI，由于S2＝SRt△DOI，S△BOC＝S△MND，得出S2+S4＝SRt△ABC，S3＝S△ABC，再证明Rt△AGE≌Rt△ACB，Rt△DNB≌Rt△BHD，由于S1+S2+S3+S4+S5＝S1+S3+（S2+S4）+S5＝Rt△ABC的面积+Rt△ABC的面积+Rt△ABC的面积+Rt△ABC的面积＝Rt△ABC的面积×4，据此即可求解.
【解析】【解答】解：需要添加的条件是：AC⊥BD，理由如下：
∵对角线AC，BD交于点O，OA=OC=OB=OD，
∴四边形ABCD是矩形，
又∵AC⊥BD，
∴矩形ABCD是正方形.
故答案为：AC⊥BD.（答案不唯一）
【分析】根据OA=OC=OB=OD，可判定四边形ABCD为矩形，因此根据对角线相互垂直的矩形为为正方形，添加AC⊥BD即可，也可以根据有一组邻边相等的矩形是正方形添加条件.
【解析】【解答】解：由勾股定理得：AC2＋BC2＝AB2，
∴S3＝S2＋S1，
∴S2＝S3−S1＝39−15＝24.
故答案为：24.
【分析】由勾股定理结合正方形的性质可得S3＝S2＋S1，据此进行解答.
【解析】【解答】解：分别过点，，，作轴，轴，轴于点，，，

，
， ， ， ，
可得出 ，
，
， ， ， ，
可得 ， ，
同理可得出： ， ， ， ，
， ， ， 的横坐标分别为： ， ， ， ，
点 的横坐标为： ，
， ， ， 的纵坐标分别为：1， ， ， ， ，
点 的纵坐标为： ，
点 的坐标为 ；点 的坐标为： ， .
故答案为： ， .
【分析】分别过点B1、B2、B3，作B1D⊥x轴，B2E⊥x轴，B3F⊥x轴于点D、E、F，易得B1（2，1），B2（，），B3（8，2），B4（，），推出Bn的坐标，据此解答.
【解析】【解答】解： 四边形ABCD是菱形， ， ，
，
，
则阴影部分的面积为： ，
，
，
故答案为： .
【分析】根据菱形的对角线互相垂直平分可得OA=AC=4，OB=BD=3，OA⊥OB，由勾股定理求出AB，然后根据S阴影=S半圆-S△AOB进行计算.
【解析】【解答】解：连接OE，OF，ON，OG，

在矩形ABCD中，
∵∠A＝∠B＝90°，CD＝AB＝8，
∵AD，AB，BC分别与⊙O相切于E，F，G三点，
∴∠AEO＝∠AFO＝∠OFB＝∠BGO＝90°，
∴四边形AFOE，FBGO是正方形，
∴AF＝BF＝AE＝BG＝4，
∴DE＝6，
∵DM是⊙O的切线，
∴DN＝DE＝6，MN＝MG，
∴CM＝10﹣4﹣MN＝6﹣MN，
在Rt△DMC中，DM2＝CD2+CM2，
∴（6+NM）2＝（6﹣NM）2+82，
∴NM＝ ，
∴DM＝6+ ＝ .
故答案为： .

【分析】连接OE，OF，ON，OG，根据矩形性质得∠A＝∠B＝90°，CD＝AB＝8，由切线性质可得∠AEO＝∠AFO＝∠OFB＝∠BGO＝90°，可证明四边形AFOE，FBGO是正方形，得AF＝BF＝AE＝BG＝4，进而求得DE＝6；根据切线长定理可得DN＝DE＝6，MN＝MG，可求得CM＝6﹣MN，再在Rt△DMC中，由勾股定理得DM2＝CD2+CM2，即（6+NM）2＝（6﹣NM）2+82，求得NM＝ ，进而可求出DM的长.
【解析】【解答】解：如图所示，对需要的交点标注字母：

，


，
，
∴，
，
∵，
∴，
化简得：，
∴.
故答案为：.
【分析】对图形进行点标注，根据三角形的面积公式可得S△DGI，S△MNC，根据S△KMD=S△BCD-S△DMC-S△DKA-S△KBM可得S△KMD，然后表示出S1、S2，接下来根据S1=6S2就可得到 的值.
【解析】【解答】解：正方形ABCD中，BC=CD=4， ，连接BD，交EF于点O，如图所示：

则 ，
在 中，由勾股定理，得： ，
∵EF平分正方形ABCD的面积，
∴EF一定经过正方形得中心，即点O是正方形的中心，
∴ ，
∵EF⊥BP交BP于G，
∴ ，
∴以OB为直径作 ，如上图，则点G在 上， ，
∴连接CM，如上图，则点G在CM与 的交点处时，CG的值最小，
此时， ，
过点M 作MN⊥BC于点N，如上图，则 ，
在 中， ，
，
∴ ，
在 中，由勾股定理，得： ，
∴ ，
即 的最小值是 .
故答案为： .
【分析】连接BD，交EF于点O，则∠ABD=∠CBD=45°，由勾股定理求出BD，由题意可得EF一定经过正方形的中心，据此可得OB=OD，以OB为直径作 ，则点G在上， 可得BM=GM=，连接CM，则点G在CM与的交点处时，CG的值最小，此时MG=BM=，过点M 作MN⊥BC于点N，利用三角函数的概念可得BN、MN，进而求出CN，由勾股定理求出CM，然后根据CG=CM-MG进行计算.
【解析】【解答】解：如图，以AB的中点为圆心，以AB为直径画圆，

∵∠AFB为90°，
∴F点在圆周上，
当C、F、O在一条直线上时，CF最短，
∵，
∴ .
如图，H在以BC的中点N为圆心，以2为半径的圆上，轨迹是弧BH'，G点在以M为圆心，以为半径的圆上，轨迹是弧BC，

则线段HG扫过的面积=S阴影=S△BCH-(S扇形MBC-S△MBC)+S扇形NBH'-S△NBH'
=×4×2-(2π-4)+π-2
=6-π.
故答案为： 6-π .
【分析】以AB的中点为圆心，以AB为直径画圆，由直角所对的圆周角是直角得出点F圆周上，则知当C、F、O在一条直线上时，CF最短，再根据勾股定理求出OC，最后根据线段间的和差关系求CF长即可；根据题意可知，H在以BC的中点N为圆心，以2为半径的圆上，轨迹是弧BH'，G点在以M为圆心，以为半径的圆上，轨迹是弧BC，线段HG扫过的面积=S阴影=S△BCH-(S扇形MBC-S△MBC)+S扇形NBH'-S△NBH'，依此计算，即可求出结果.
【解析】【解答】解：分两种情况：
①如图1，∠D'AB'＝90°，延长C'B'交AB于G，过点D'作D'H⊥AB，交BA的延长线于H，

∴∠H＝∠AGB'＝∠BGB'＝90°，
∵四边形ABCD是矩形，
∴∠BAD＝∠C＝90°，AD＝BC＝3，
∵tan∠ABD＝ ，即 ，
设B'G＝3x，BG＝4x，
∴BB'＝a＝5x，
由平移得：DD'＝BB'＝5x，
∴D'H＝3+3x，AH＝BG＝4x，
∴AG＝AB＝BG＝4﹣4x，
∵∠D'AB'＝∠HAD'+∠BAB'＝90°，
∠AD'H+∠HAD'＝90°，
∴∠AD'H＝∠GAB'，
∵∠H＝∠AGB'＝90°，
∴△D'HA∽△AGB'，
∴ ，即 ，
∴x＝ ，
∴a＝5× ＝ ；
②如图2，∠AB'D'＝90°，延长C'B'交AB于M，则C'M⊥AB，

∴∠AMB'＝90°，
由平移得：B'C'＝BC＝3，
同理设B'M＝3m，BM＝4m，则BB'＝a＝5m，
∴AM＝4﹣4m，
∵∠AB'M+∠D'B'C'＝90°，∠MAB'+∠AB'M＝90°，
∴∠D'B'C'＝∠MAB'，
∵∠C'＝∠AMB'＝90°，
∴△D'C'B'∽△B'MA，
∴ ，即 ，
∴m＝ ，
∴a＝5m＝5× ＝ ；
综上，a的值是 或 .
故答案为： 或 .
【分析】①当∠D'AB'＝90°时，延长C'B'交AB于G，过点D'作D'H⊥AB，交BA的延长线于H，由矩形的性质可得∠BAD＝∠C＝90°，AD＝BC＝3，根据∠ABD的正切函数可设B'G＝3x，BG＝4x，则BB'＝a＝5x，由平移得：DD'＝BB'＝5x，则D'H＝3+3x，AH＝BG＝4x，AG＝AB＝BG＝4-4x，证明△D'HA∽△AGB'，然后根据相似三角形的性质求出x，据此可得a的值；②当∠AB'D'＝90°时，延长C'B'交AB于M，则C'M⊥AB，由平移得：B'C'＝BC＝3，同理设B'M＝3m，BM＝4m，则BB'＝a＝5m，则AM＝4-4m，证明△D'C'B'∽△B'MA，由相似三角形的性质求出m，进而可得a的值.
【解析】【解答】解：过A点作AH⊥BD于H，连接OM，如图：

∵四边形ABCD是矩形，
∴∠BAD＝90°，
在Rt△ABD中，BD＝＝＝25，
∵×AH×BD＝×AD×AB，
∴AH＝＝12，
∵⊙O的直径为16，
∴⊙O的半径为8，
∴点O在AH上时，OH最短，
∵HM＝，
∴此时HM有最大值，OH＝AH﹣OA＝4，
则最大值为＝4，
∵OH⊥MN，
∴MN＝2MH，
∴MN的最大值为2×4＝8．
故答案为：8．

【分析】过A点作AH⊥BD于H，连接OM，根据四边形ABCD是矩形，在Rt△ABD中，利用勾股定理得出BD的值，点O在AH上时，OH最短，得出此时HM有最大值，即可得出结论。
【解析】【分析】（1）由已知条件可得四边形ADCE是平行四边形，根据直角三角形斜边上中线的性质可得CD=AB=AD，然后利用有一组邻边相等的平行四边形是菱形进行证明；
（2）过点D作DF⊥CE，垂足为点F，易得△BCD是等边三角形，则∠BDC=∠BCD=60°，CD=BC=6，根据平行线的性质可得∠DCE=∠BDC=60°，则∠CDF=30°，根据含30°角的直角三角形的性质可得CF=3，然后在Rt△CDF中，应用勾股定理求解即可.
【解析】【分析】（1）根据矩形的性质易证DC∥AB，DC=AB，再证明DE=BF，然后根据有一组对边平行且相等的四边形是平行四边形，可证结论。
（2）利用菱形的性质可得到AF=FC，设AF=FC=x，则BF=6-x，利用勾股定理建立关于x的方程，解方程求出x的值。
【解析】【分析】根据三角形中位线的性质可得 GH＝AD，HE＝BC，FG＝BC， 再结合AD=BC，即可得到EF＝GH＝HE＝FG，因此四边形EFGH是菱形．
【解析】【分析】 连接B′B，作B′E⊥BC于E， 利用矩形的性质得出 ∠CBB′=75°，∠CBB′=∠CB′B=75°， 再利用旋转的性质得出答案。
【解析】【分析】先证明DE=DC，DF=DC，则DE=DF，再证明四边形AECF是平行四边形，然后证明∠ECF=90°，即可得出结论。
【解析】【解答】（1）【探究发现】 .
【分析】（1）【探究发现】 .
（2）（验证猜想） 过点A作 ，交CD的延长线于点G. 先证明 ，可得 ， ， 再证明 ，可得，即得；
（3）（迁移应用）连接EF，设DF的长为，可得 ，根据【验证猜想】可得 ， 在 中，根据勾股定理建立方程，求解即可.
【解析】【分析】 （Ⅰ） 根据题意求出AD的长，由矩形的性质得DE∥OC， 求出∠AED的度数，根据勾股定理求出ED的长度，即可求出点E的坐标 ；
（Ⅱ） ①由平移的性质及勾股定理，求出FE′= t，从而求出△MFE′的面积，再求出矩形C′O′D′E′的面积， 利用 S＝S矩形C′O′D′E′﹣S△MFE′，即可求解； ②当S＝ 时， 根据题意列出方程 （6﹣t）× （6﹣t）＝ ， 求出方程的解并进行检验； 当S＝5 时，根据题意列出方程 [ （6﹣t）+ （4﹣t）]×2＝5 ， 求出方程的解，再由 ≤S≤5 ，即可求出t的取值范围.
【解析】【分析】 延长 至 ，使 ，连接 ，如图所示： 则 ， ， 首先判断出 是等腰直角三角形， 根据等腰直角三角形的性质得出 ， 然后根据角平分线的定义，正方形的性质及邻补角的定义判断出 ，三点共线， 用SAS判断出 根据全等三角形的性质得出 ，进而根据等量代换及等边对等角得出 ， 根据角的和差及三角形的外角定理等式的性质得出 ，根据直角三角形两锐角互余及等量代换得出 ， 最后根据平角的定义即可得出结论。
【解析】【解答】 (1)解：如图，设直线BC与直线 的交点为H， 交BH于O.

根据题意得：△ABC∽ ， ， ， ，
∴ ，
∵ ， ，
∴ ，
故答案为：7，40.
【分析】（1）根据题意得△ABC∽ ，根据变换 的定义及相似三角形的性质即可求解；（2）根据矩形的性质可求出 ， 根据含30°直角三角形的性质可得 ，继而得解；
（3） 根据平行线四边形的性质可得 ，再证明 可得
，据此求出AB，从而得出 ，利用 求出n值.
【解析】【解答】解：（1）如图1，延长DF分别交BE于点G，

在正方形ABCD和等腰直角△AEF中，AD=AB，AF=AE，∠BAD=∠EAF=90°，
∴∠FAD=∠EAB，
∴△FAD≌△EAB（SAS），
∴∠AFD=∠AEB，DF=BE，
∵∠AFD+∠AFG=180°，
∴∠AEG+∠AFG=180°，
∵∠EAF=90°，
∴∠EGF=180°-90°=90°，
∴DF⊥BE，
∴=1，β=90°，
故答案为：1，90°；
（3）①如图3，延长DF交EB的延长线于点H，

∵AD=kAB，AF=kAE，
∴，
∵∠BAD=∠EAF=α，
∴∠FAD=∠EAB，
∴△FAD∽△EAB，
∴，
∴，
②由△FAD∽△EAB得∠AFD=∠AEB，
∵∠AFD+∠AFH=180°，
∴∠AEB+∠AFH=180°，
∵四边形AEHF的内角和为360°，
∴∠EAF+∠EHF=180°，
∴α+β=180°．
【分析】（1）如图1，延长DF分别交BE于点G，证明△FAD≌△EAB（SAS），可得∠AFD=∠AEB，DF=BE，从而得出∠AEG+∠AFG=180°，利用四边形内角和求出∠EGF=90°，继而得解；
（2） 如图2，延长DF交EB于点H，证明△FAD∽△EAB，可得， ∠AFD=∠AEB， 从而得出∠AEH+∠AFH=180°，利用四边形内角和求出∠EHF=90°，继而得解；
（3）①延长DF交EB的延长线于点H，证明△FAD∽△EAB，可得，即得结论；②由△FAD∽△EAB得∠AFD=∠AEB，由∠AFD+∠AFH=180°可得∠AEB+∠AFH=180°，根据四边形的内角和可求出∠EAF+∠EHF=180°，即得结论.