2022届河南省信阳市中招数学一模试卷解析版

这是一份2022届河南省信阳市中招数学一模试卷解析版，共25页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


河南省信阳市中招数学一模试卷
一、单选题
1．－2022的倒数是（　　）
A．－2022 B．2022 C． D．
2．下列问题中，适合抽样调查的是（　　）
A．“双十一”期间某网店的当日销售额
B．神舟十三号飞船的零部件检查
C．“7•20”特大暴雨河南省受损的农作物面积
D．东京奥运会乒乓球比赛用球的合格率
3．下列几何体的三视图中，俯视图与主视图一定一致的是（　　）
A． B．
C． D．
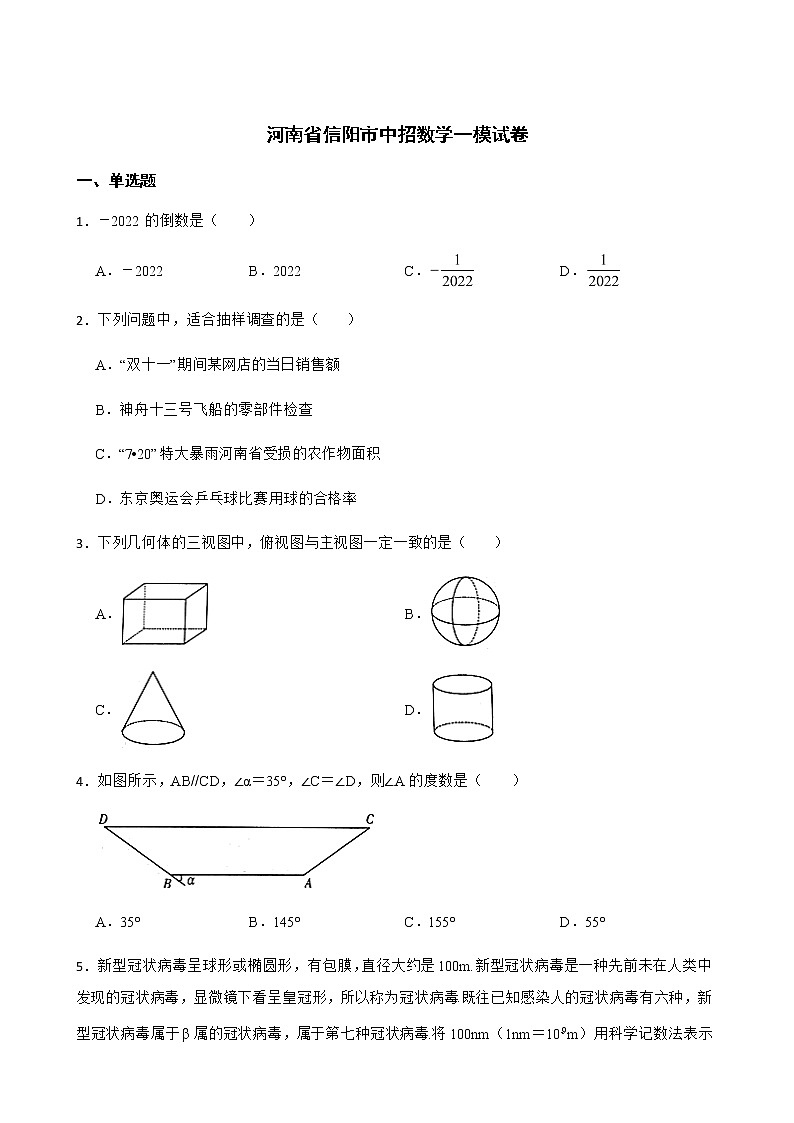
4．如图所示，AB//CD，∠α＝35°，∠C＝∠D，则∠A的度数是（　　）

A．35° B．145° C．155° D．55°
5．新型冠状病毒呈球形或椭圆形，有包膜，直径大约是100m.新型冠状病毒是一种先前未在人类中发现的冠状病毒，显微镜下看呈皇冠形，所以称为冠状病毒.既往已知感染人的冠状病毒有六种，新型冠状病毒属于β属的冠状病毒，属于第七种冠状病毒.将100nm（1nm＝10﹣9m）用科学记数法表示为（　　）
A．1×10﹣7m B．1×10﹣8m C．1×10﹣9m D．1×10﹣6m
6．《九章算术》是中国古代数学著作之一，书中有这样的一个问题：今有甲、乙二人持钱不知其数.甲得乙半而钱五十，乙得甲太半而钱亦五十.问甲、乙持钱各几何？题意为：今有甲、乙二人，不知其钱包里有多少钱.若乙把其一半的钱给甲，则甲的钱数为50；而甲把其的钱给乙，则乙的钱数也能为50，问甲、乙各有多少钱？解：设甲原有钱数为x，乙原有钱数为y，依题意可得方程组为（　　）
A． B．
C． D．
7．将分别标有“中”“国”…“全”“面”“小”“康”汉字的六个小球装在一个不透明的口袋中，这些球除汉字外无其他差别，每次摸球前先搅拌均匀，随机摸出一球，然后放回，再随机摸出一球，两次摸出的球上的汉字是“小”和“康”的概率是（　　）
A． B． C． D．
8．函数 的图象如图所示，则关于x的一元二次方程 的根的情况是（　　）

A．没有实数根 B．有两个相等的实数根
C．有两个不相等的实数根 D．无法确定
9．如图，在平面直角坐标系中放置一菱形OABC，已知∠ABC＝60°，点B在y轴上，OA＝1，将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2021次，点B的落点依次为B1，B2，B3，……，则B2021的坐标为（　　）

A．（1010，0） B．（1345，）
C．（，） D．（1346，0）
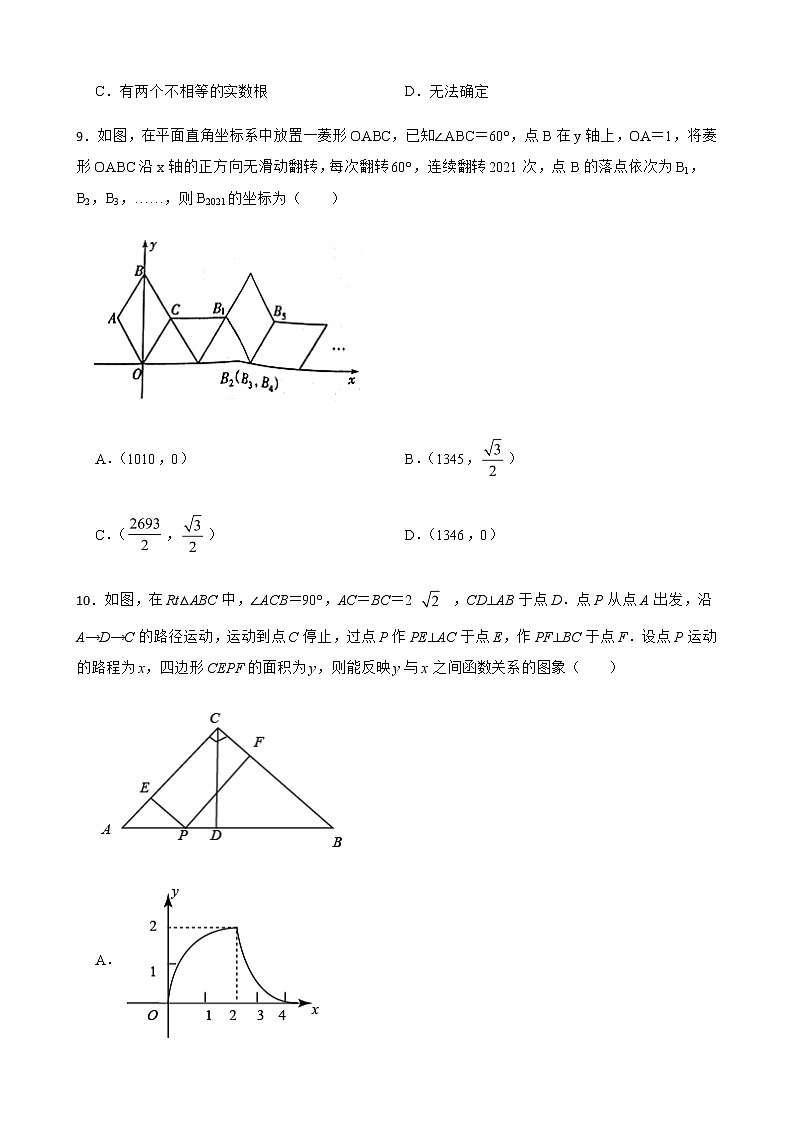
10．如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝2 ，CD⊥AB于点D．点P从点A出发，沿A→D→C的路径运动，运动到点C停止，过点P作PE⊥AC于点E，作PF⊥BC于点F．设点P运动的路程为x，四边形CEPF的面积为y，则能反映y与x之间函数关系的图象（　　）

A．
B．
C．
D．
二、填空题
11．请写出一个大于3小于5的无理数：　 　.
12．某函数满足当自变量x＝1时，函数值y＝0.写出一个满足条件的一次函数表达式：　 　.
13．如图所示，在△ABC中，∠B＝90°，AB＝BC＝4，D，E，F分别是AC，BC，AB边上的点，且∠EDF＝45°，DE＝DF，则AF+CE＝　 　.

14．如图，图1是由若干个相同的图形（图2）组成的美丽图案的一部分，图2中，图形的相关数据：半径OA=2cm，∠AOB=120°．则图2的周长为　 　cm（结果保留π）．

15．在矩形ABCD中，AB＝4，BC＝2，点E在线段BC上，连接AE，过点B作BF⊥AE交线段CD于点F.以BE和BF为邻边作平行四边形BEHF，当点E从B运动到C时，点H运动的路径长为　 　.

三、解答题
16．
（1）计算：；
（2）化简：.
17．2021年秋季教育部明确提出，要减轻义务教育阶段学生的作业负担，学生的校外培训负担.依据政策要求，初中书面作业平均完成时间不超过90分钟，学生每天的完成作业时长不能超过2小时.某中学为了积极推进教育部的新政策实施，对本校学生的作业情况进行了抽样调查，统计结果如图所示：

（1）这次抽样共调查了 ▲ 名学生，并补全条形统计图；
（2）计算扇形统计图中表示作业时长为2.5小时对应的扇形圆心角度数；
（3）若该中学共有学生3000人，请据此估计该校学生的作业时间不少于2小时的学生人数；
（4）通过本次调查，你认为该学校作业布置是否满足教育部的“双减”政策要求？请说明理由，并给出相应的建议.
18．弦切角定理（弦切角等于它所夹的弧所对的圆周角）在证明角相等、线段相等、线段成比例等问题时，有非常重要的作用，为了说明弦切角定理的正确性，小明同学进行了以下探索过程：
问题的提出：若一直线与圆相交，过交点作圆的切线，则此切线与直线的交角中的任意一个称为直线和圆的交角，其中所夹弧为劣弧的角为劣交角，所夹弧为优弧的角为优交角.直线和圆的交角有以下性质：直线和圆的交角等于所夹弧所对的圆周角.
问题的证明：（只证明劣交角即可）

（1）请将不完整的已知和求证补充完整，并写出证明过程；
已知：如图1，直线l与⊙O相交于点A，B，过点B作 ▲ .
求证：∠ABD＝ ▲ .
（2）如图2，直线l与⊙O相交于点A，B，AD为⊙O的直径，BC切⊙O于点B，交DA的延长线于点C，若AD＝BC，AC＝2，求⊙O的半径.
19．如图，点P为函数与函数图象的交点，点P的纵坐标为4，轴，垂足为点B.

（1）求m的值；
（2）点M是函数图象上一动点，过点M作于点D，若，求点M的坐标.
20．某汽车贸易公司销售A，B两种型号的新能源汽车，A型车进货价格为每台12万元，B型车进货价格为每台15万元，该公司销售2台A型车和5台B型车，可获利3.1万元，销售1台A型车和2台B型车，可获利1.3万元.
（1）求销售一台A型、一台B型新能源汽车的利润各是多少万元？
（2）该公司准备用300万元资金，采购A，B两种新能源汽车，可能有多少种采购方案？
（3）该公司准备用不超过300万，采购A，B两种新能源汽车共22台，问最少需要采购A型新能源汽车多少台？
21．小明根据学习函数的经验，对函数y＝|x2﹣2x|﹣2的图象与性质进行了探究，下面是小明的探究过程，请补充完整：
x
…
﹣2
﹣1
0
1
2
3
4
…
y
…
6
m
﹣2
﹣1
﹣2
n
6
…

（1）在给定的平面直角坐标系中；画出这个函数的图象，
①列表，其中m＝ ▲ ，n＝ ▲ .
②描点：请根据表中数据，在如图所示的平面直角坐标系中描点：
③连线：画出该函数的图象.
（2）写出该函数的两条性质：　 　.
（3）进一步探究函数图象，解决下列问题：
①若平行于x轴的一条直线y＝k与函数y＝|x2﹣2x|﹣2的图象有两个交点，则k的取值范围是 　 　；
②在网格中画出y＝x﹣2的图象，直接写出方程|x2﹣2x|﹣2＝x﹣2的解为 　 　.
22．如图，直线与x轴交于点A（3，0），与y轴交于点B，抛物线经过点A，B.

（1）求点B的坐标和抛物线的表达式；
（2）P（x1，y1），Q（4，y2）两点均在该抛物线上，若y1≥y2，求P点的横坐标x1的取值范围；
（3）点M为直线AB上一动点，将点M沿与y轴平行的方向平移一个单位长度得到点N，若线段MN与抛物线只有一个公共点，直接写出点M的横坐标的取值范围.
23．在△ABC中，∠ACB＝90°，AC＝BC，点D是直线AB上的一动点（不与点A，B重合），连接CD，在CD的右侧以CD为斜边作等腰直角三角形CDE，点H是BD的中点，连接EH.

（1）如图1，当点D是AB的中点时，线段EH与AD的数量关系是 　 　，EH与AD的位置关系是 　 　；
（2）如图2，当点D在边AB上且不是AB的中点时，（1）中的结论是否仍然成立？若成立，请仅就图2中的情况给出证明；若不成立，请说明理由；
（3）若AC＝BC＝2，其他条件不变，连接AE，BE.当△BCE是等边三角形时，请直接写出△ADE的面积.
答案解析部分
【解析】【解答】解：－2022的倒数是.
故答案为C.
【分析】根据倒数的定义求解即可。
【解析】【解答】解：A、 “双十一”期间某网店的当日销售额，适合普查，故选项A不合题意；
B、 神舟十三号飞船的零部件检查，适合普查，故选项B不合题意；
C、“7•20”特大暴雨河南省受损的农作物面积，适合普查，故选项C不合题意；
D、 东京奥运会乒乓球比赛用球的合格率，适合抽样调查，故选项D符合题意.
故答案为：D.
【分析】全面调查数据准确，但耗时费力；抽样调查省时省力，但数据不够准确；一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时，应选择抽样调查；对于精确度要求高的调查，事关重大的调查往往选用普查，据此判断即可.
【解析】【解答】解：A、俯视图为矩形，主视图也是矩形，
但是由于矩形的长宽高的具体值不知道，
因此俯视图和主视图不能一定判断一致，
故此选项错误，不符合题意；
B、俯视图为圆形，主视图也是圆形，
因为是一个球形，所以球的半径都是一致的，
因此主视图和俯视图一定是一致的，
故此选项正确，符合题意；
C、俯视图为圆形，并且圆形中心有一个点，主视图为三角形，
因此俯视图和主视图不一致，
故此选项错误，不符合题意；
D、俯视图为圆形，主视图为矩形，
因此俯视图和主视图不一致，
故此选项错误，不符合题意.
故答案为：B.
【分析】主视图就是从正面看得到的图形；俯视图就是从左面看得到的图形；据此判断出长方体、球、圆锥、圆柱的俯视图与主视图，然后进行判断.
【解析】【解答】解：∵AB//CD，
∴∠D=∠α=35°，
∵∠C＝∠D，
∴∠C=35°，
∵AB//CD，
∴∠C+∠A=180°，
∴∠A=180°-∠C=180°-35°=145°.
故答案为：B.
【分析】根据二直线平行，同位角相等得∠D=∠α=35°，结合∠C=∠D可得∠C=35°，由二直线平行，同旁内角互补得∠C+∠A=180°，据此计算.
【解析】【解答】解：100nm（1nm＝10﹣9m）用科学记数法表示为m.
故答案为：A.
【分析】用科学记数法表示绝对值非常小的数，一般表示成a×10-n的形式，其中1≤∣a∣＜10，n等原数左边第一个非0数字前面所有0的个数，包括小数点前面的那个0，根据方法即可得出答案.
【解析】【解答】解：设甲原有钱数为x，乙原有钱数为y，根据题意得：
.
故答案为：C.
【分析】设甲原有钱数为x，乙原有钱数为y，根据甲得乙半而钱五十可得方程x+ y=50；根据乙得甲太半而钱亦五十可得方程 x+y=50，联立可得方程组,
【解析】【解答】解：画树状图如下：

共有36种等可能结果，其中，两次摸到的球上的汉字是“小”和“康”的结果有2种
两次摸到的球上的汉字是“小”和“康”的概率为 .
故答案为：D.
【分析】此题是抽取放回类型，画出树状图，找出总情况数以及两次摸到的球上的汉字是“小”和“康”的情况数，然后利用概率公式进行计算.
【解析】【解答】解：观察函数图象可知：函数y=kx+b的图象经过第二、三、四象限，
∴k＜0，b＜0.
在方程 中，
△= ，
∴一元二次方程 有两个不相等的实数根.
故答案为：C.
【分析】由直线所在的象限可知k＜0，b＜0；然后计算关于x的一元二次方程的b2-4ac的值，由平方的非负性可知b2-4ac＞0，再根据一元二次方程的根的判别式“①当b2-4ac＞0时，方程有两个不相等的实数根；②当b2-4ac=0时，方程有两个相等的实数根；③当b2-4ac＜0时，方程没有实数根”可判断求解.
【解析】【解答】解：如图，连接AC，

∵四边形OABC是菱形，
∴，
∵，
∴是等边三角形，
∴，
∴，
∵，
∴，
画出第5次，第6次，第7次，翻转后的图形，
由图可知，每翻转6次，图形向右平移4个单位长度，
∵2021=336×6＋5，
∴点 向右平移1344（即336×4）个单位长度到点 ，
∵点 的坐标为 ，
∴点 的坐标为 ，
∴点 坐标为 .
故答案为：C.
【分析】连接AC，根据菱形的性质可得OA=AB=BC=OC，推出△ABC是等边三角形，得AC=AB，则AC=OA=1，画出第5次，第6次，第7次翻转后的图形，得到B5的坐标，然后根据B5向右平移1344个单位长度得到B2021就可得到对应的坐标.
【解析】【解答】解：∵在Rt△ABC中，∠ACB＝90°，AC＝BC＝2 ，
∴ ，
∵CD⊥AB，
∴ ，
∵PE⊥AC，PF⊥BC，
∴四边形CEPF是矩形，
∴ ，
∵点P运动的路程为x，
∴当点P从点A出发，沿A→D路径运动时，即 ， ，
∴ ，
∴ ，
∴四边形CEPF的面积为 ，
∴当 时，抛物线开口向下；
当点P沿D→C路径运动时，即 ，
∵CD是∠ACB的平分线，
∴PE=PF，
∴四边形CEPF是正方形，
∵AD=2，PD=x-2，
∴CP=4-x，
∴ ，
∴当 时，抛物线开口向上，
综上所述：能反映y与x之间函数关系的图象只有A选项符合；
故答案为：A．
【分析】先求出 ，再求出 ，最后求解即可。
【解析】【解答】解：∵，，
∴进行平方运算后结果在9到25之间的无理数都满足条件，
故满足条件的数有： ， ， 等，
故答案为： （任选一个满足条件的无理数即可）.
【分析】只要写出的正无理数的平方在9到25之间即可.
【解析】【解答】解：设一次函数解析式为
将 ，代入解得
∴一次函数解析式为y=x-1
故答案为：y=x-1.
【分析】设一次函数的解析式为y=x+b，将x=1、y=0代入求出b的值，进而可得函数解析式.
【解析】【解答】解：AB=BC=4，∠B=90°，
∴是等腰直角三角形，
∴AC= ；
中∠A＋∠AFD＋∠ADF=180°，∠A=45°，
∴∠AFD＋∠ADF=135°，
直线AC上∠CDE＋∠EDF＋∠ADF=180°，∠EDF=45°，
∴∠CDE＋∠ADF=135°，
∴∠AFD=∠CDE，
又∵∠A=∠C，DF=DE，
∴（AAS）
∴AF=CD，AD=CE，
∴AF+CE＝CD+AD=AC= .
故答案为： .
【分析】易得△ABC是等腰直角三角形，AC= ，根据内角和定理可得∠AFD＋∠ADF=135°，根据平角的概念可得∠CDE＋∠ADF=135°，推出∠AFD=∠CDE，然后利用AAS证明△AFD≌△CDE，得到AF=CD，AD=CE，据此计算.
【解析】【解答】解：由图1得： 的长+ 的长= 的长，
∵半径OA=2cm，∠AOB=120°
则图2的周长为： .
故答案为 ．
【分析】先根据图1确定：图2的周长=2个 的长，根据弧长公式可得结论．
【解析】【解答】解：如图，连接CH.

∵四边形ABCD是矩形，
∴∠ABC=∠BCF=90°，
∵BF⊥AE，
∴∠ABF+∠EBF=90°，∠ABF+∠EAB=90°，
∴∠EAB=∠CBF，
∴△ABE∽△BCF，
∴=2，
∵四边形BEHF是平行四边形，
∴FH=BE，FH∥BE，
∴∠HFC=∠BCF=90°，
∴=2，
∴tan∠HCF=2，
∴∠HCF是定值，
∴点H的运动轨迹是线段CH，
当点E从B运动到C时，
∴FH=BC=2，
∴CF=1，
∴CH= .
故答案为： .
【分析】连接CH，根据矩形的性质得∠ABC=∠BCF=90°，根据同角的余角相等得∠EAB=∠CBF，证明△ABE∽△BCF，由平行四边形的性质得FH=BE，FH∥BE，由平行线的性质得∠HFC=∠BCF=90°，然后求出tan∠HCF的值，推出点H的运动轨迹是线段CH，据此计算.
【解析】【分析】（1）根据算术平方根的概念、0次幂以及负整数指数幂的运算性质分别计算，然后根据有理数的加减法法则进行计算；
（2）首先对第一个分式的分母进行分解因式，对第二个分式的分子进行分解因式，然后将除法化为乘法，再约分可对前两项进行化简，接下来根据异分母分式减法法则计算即可.
【解析】【解答】解：（1）由两幅统计图可知：部分学生完成作业所需要的时间为2小时的有140人，占调查学生总数的28％，每天完成作业所需要的时间为1.5小时的占调查学生总数的36％，
∴这次抽样共调查了140÷28％=500（名）学生，
∴每天完成作业所需要的时间为1.5小时的有500×36％=180人.
故答案为：500；
【分析】（1）利用完成作业需要时间为2小时的人数除以所占的比例可得总人数，利用总人数乘以完成作业需要时间为1.5小时的人数所占的比例可得对应的人数，据此补全条形统计图；
（2）利用完成作业需要时间为2.5小时的人数除以总人数，然后乘以360°即可；
（3）首先求出样本中完成作业需要时间不少于2小时的人数所占的比例，然后乘以3000即可；
（4）求出每天完成作业时长超过2小时的学生所占的比例，作业平均完成时间，据此解答.
【解析】【解答】解： （1）由题意知：
已知：如图1，直线l与⊙O相交于点A，B，过点B作 的切线 .
求证：∠ABD＝ .
故答案为： 的切线 ，∠ABD＝ ；
【分析】（1）连接OA、OB、OC，由切线的性质得∠OBD=90°，故∠ABD=90°-∠OBA，容易得∠OAB=∠OBA，∠OCA=∠OAC，∠OCB=∠OBC，结合内角和定理得∠OCA+∠OCB=90°-∠OBA，然后根据∠ACB=∠OCA+∠OCB=90°-∠OBA即可得到结论；
（2）连接BD，易证△ABC∽△BDC，根据相似三角形的性质可得BC，进而可得半径.
【解析】【分析】（1）将y=4代入y=x+1中求出x的值，得到点P的坐标，然后代入y=中就可求出m；
（2）根据三角函数的概念可设PD=t，则PM=2t，当M点在P点右侧时， M（6+2t，4-t），根据点M在反比例函数的图象上可得t的值，得到点M的坐标；当M点在P点的左侧时，M（6-2t，4+t），同理可得t的值，得到点M的坐标.
【解析】【分析】（1）设一台A型、一台B型新能源汽车的利润分别为x、y万元，根据销售2台A型车和5台B型车，可获利3.1万元可得方程2x+5y=3.1，根据销售1台A型车和2台B型车，可获利1.3万元.可得方程x+2y=1.3，联立求解即可；
（2）设采购A，B两种新能源汽车分别为a、b台，根据300万元资金可得12a+15b=300，表示出b，然后根据a、b为正整数可得a、b的值，进而可得采购方案；
（3）设最少需要采购A型新能源汽车y台，则采购B型新能源汽车（22-y）台，根据台数y进价=总价列出关于y的不等式，求解即可.
【解析】【解答】解：（1）①将 代入解析式得
∴
将 代入解析式得
∴
故答案为：1，1；
（2）解题图象可知：①函数图象关于直线 对称；
②函数的最小值为-2；
故答案为： 图象关于直线 对称；函数的最小值为-2 ；
（3）①由图象可知：当 或 时，直线 与函数图象有两个交点；
故答案为： k＞-1或k=-2 ；
②如图3，

由题意知|x2﹣2x|﹣2＝x﹣2的解即为y＝|x2﹣2x|﹣2与y＝x﹣2图象交点的横坐标
∴由图象可知|x2﹣2x|﹣2＝x﹣2的解为 或 或 .
故答案为： x=0或x=1或x=3 .
【分析】（1）①将x=-1代入函数解析式中可得m的值；将x=3代入函数解析式中可得n的值；
②③利用描点、连线画图即可；
（2）根据对称性、最值写出两条性质即可；
（3）①根据图象解答即可；
②由题意知|x2-2x|-2＝x-2的解即为y＝|x2-2x|-2与y＝x-2图象交点的横坐标，据此解答.
【解析】【解答】解：（3）设点N在AB上方抛物线上N（x，）为满足条件的极高点，点M（x，）
∴MN=
∵MN=1，

∴
∴，
∴
当点N在AB下方抛物线上N（x， ）为满足条件的极低点，点M（x， ）
∴MN=
∵MN=1，

∴
∴，
∴
∵线段MN与抛物线只有一个公共点，
∴点M的横坐标的取值范围 或 .


【分析】（1）将A（3，0）代入y= x+a中求出a的值，据此可得直线解析式，然后令x=0，求出y的值，可得B（0，2），将A、B的坐标代入y=x2+bx+c中求出b、c的值，进而可得抛物线的解析式；
（2）将x=4代入抛物线解析式中可得y2，令y=-6，求出x的值，可得P、Q的坐标，然后判断出函数的增减性，进而可得x1的范围；
（3）设点N在AB上方抛物线上，N（x， x2+x+2）为满足条件的极高点，点M（x，x+2），表示出MN，根据MN=1可得x的值；当点N在AB下方抛物线上，N（x，x2+x+2）为满足条件的极低点，点M（x，x+2），同理可得x的值，进而可得点M的横坐标的取值范围.
【解析】【解答】解：（1）∵点D是AB的中点
∴，
∴是等腰直角三角形
∵是等腰直角三角形
∴为 中点
∵点H是BD的中点
∴是 的中位线
∴
∴
故答案为： ， ；
解：(3)分两种情况求解：①如图3，作 ，垂足为 ， ，垂足为

由题意知 ， ， ，
∴
∴，
∴
∴
由（2）知
∴

②如图4，作 ，垂足为 ， ，垂足为M， ，垂足为N， 与 的交点为 ，

由题意知
∴，
∴
∵
∴，
∴，
∴
∵
∴
∴
∴
解得
由（2）知
∴

综上所述，△ADE的面积为 或 .
【分析】（1）易得△BCD、△CDE是等腰直角三角形，则EF为△BCD的中位线，然后根据中位线的性质进行解答；
（2）过点D作DM⊥AC，垂足为M，由等腰直角三角形的性质得∠A=∠CDE=45°，AM=DM，AB= AC，AD=AM，CD=DE，根据角的和差关系可得∠ACD=∠EDH，表示出DH，证明△CDM∽△DEH，根据相似三角形的性质可得DM、EH，据此证明；
（3）①过点E作EH⊥BD，垂足为H，过点C作CM⊥AB，垂足为M，易得AB=4，CM=AM=2，
∠EAB=∠CEB=∠CBE=60°，∠EBD=75°，∠EDB=75°，∠CDM=30°，根据三角函数的概念求出MD，进而得到AD、EH，然后根据三角形的面积公式进行计算；
②作EH⊥BD，垂足为H，CM⊥AB，垂足为M，HN⊥BC，垂足为N，CE与AB的交点为O，同理求出CN、BN、CO、BO、EO的值，证明△EHO∽△CMO，根据相似三角形的性质可得EH，由（2）知AD=2EH，然后根据三角形的面积公式进行计算.