2022年北京市顺义区初中学业水平考试第一次统一练习（一模）数学试卷

顺义区2022届初三第一次统一练习

数学参考答案及评分参考

一、选择题

二、填空题

9. ；10. ； 11. ；12.；13. ；14. ；15. ；16.

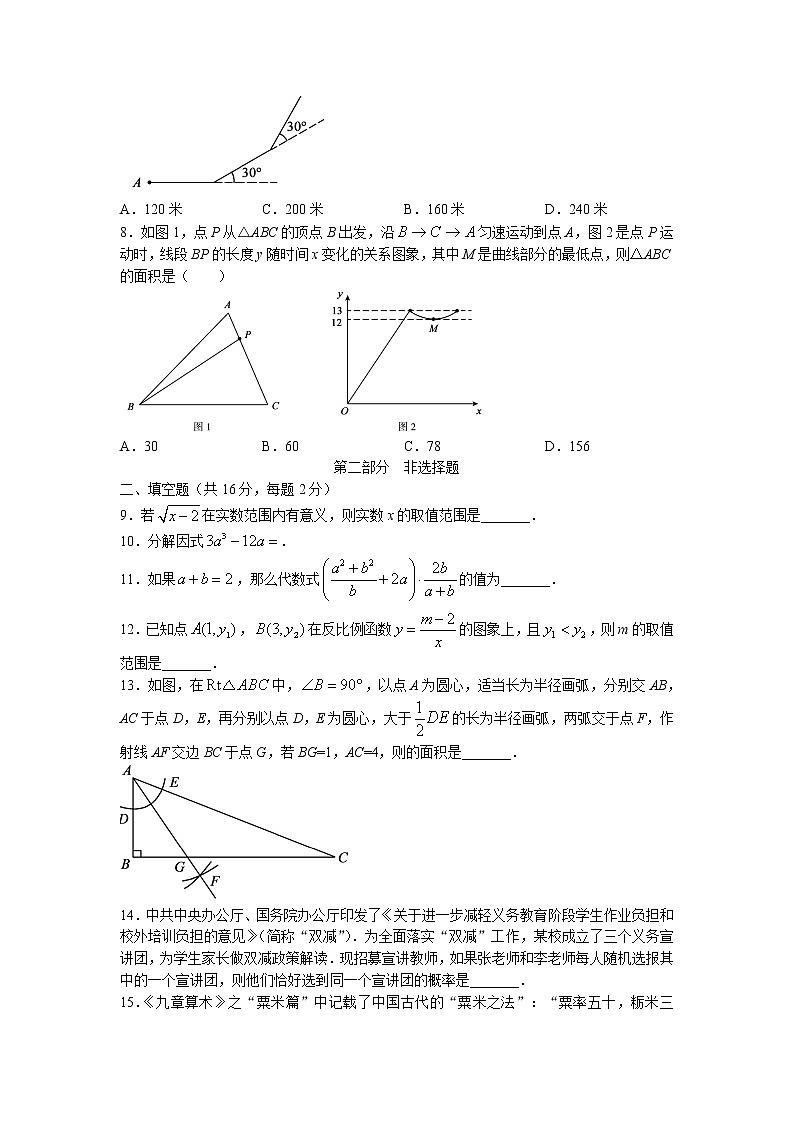
三、解答题

17. 解：原式=   …………………………………………4分

            =      ………………………………………………………………5分

18.解：解不等式，得………………………………………1分

解不等式，得   ……………………………………………2分

 所以不等式组的解集为  ……………………………………………4分

所以不等式组的所有整数解为﹣2、﹣1、0、1、2  ……………………………5分

19. 解：（1）

                                         ……………………………………………3分

（2）SSS                           ……………………………………………4分

          一条弧所对的圆周角等于它所对的圆心角的一半 ……………………………5分

        （或等边对等角，三角形的一个外角等于和它不相邻的两个内角的和）

20. 解：（1）∵关于x的一元二次方程有两个不相等的实数根

           ∴ ∆＞0 且m≠0

∆==………………………… 2分

∴ m>， 且m≠0 …………………………………………………3分

（2） ∵此方程有一个根是，

            ∴ ，

∴ ．           ………………………………………………… 4分

            ∴此方程为．

            ∴方程的另一根为．  ……………………………………………… 5分

21. （1）证明：∵ AC⊥BD， BD⊥DE ,

∴ AC∥DE.         ………………………………………………… 1分

∵ AD∥BC,

∴ 四边形ACED是平行四边形. ……………………………………… 2分

    （2）解： ∵ 四边形ACED是平行四边形,

∴ CE=AD=2 ， DE=AC=4.

∵  AC∥DE,

∴ ∠E=∠ACB.      

∴ cosE=cos∠ACB=.  …………………………………………………3分

在Rt△AED中

∵  cosE=,        ………………………………………………… 4分

∴ .

∴  BE=5.

∴  BC=BE－CE=5－2=3. …………………………………………………5分

22. 解：（1）∵ 一次函数的图象平行于直线，且经过点A(2 ，2)．

           ∴            …………………………………………………2分

 解得

           ∴ 这个一次函数的表达式为 …………………………………3分

（2）        …………………………………………………………5分

23. （1）证明：∵ 为的直径，切于A ，

              ∴ AB⊥AF，∠ADB=90°.     ……………………………………1分

              ∴ ∠BAF=90°.

∴ ∠DAF+∠DAB=90° ∠DBA+∠DAB=90°.

∴ ∠DAF=∠DBA.   ………………………………………………2分

∵ 点D为的中点,

∴ .

∴ ∠DBA=∠DAC.

∴ ∠DAC=∠DAF.    …………………………………………………3分

∵ ∠ADB=∠ADF=90º ，AD=AD,

∴△ADE≌△ADF.

∴ AE=AF.      …………………………………………………………4分

（2）解：∵ ∠DAF=∠DBA  , ∠F=∠F,

         ∴  △ADF∽△BAF

         ∴      ………………………………………………………5分

         ∵  AF=6 , BF=10

         ∴  DF=3.6

         ∵  △ADE≌△ADF

         ∴  DE=DF=3.6

         ∴  DE=BF－DF－DE=10－3.6－3.6=2.8  ………………………………6分

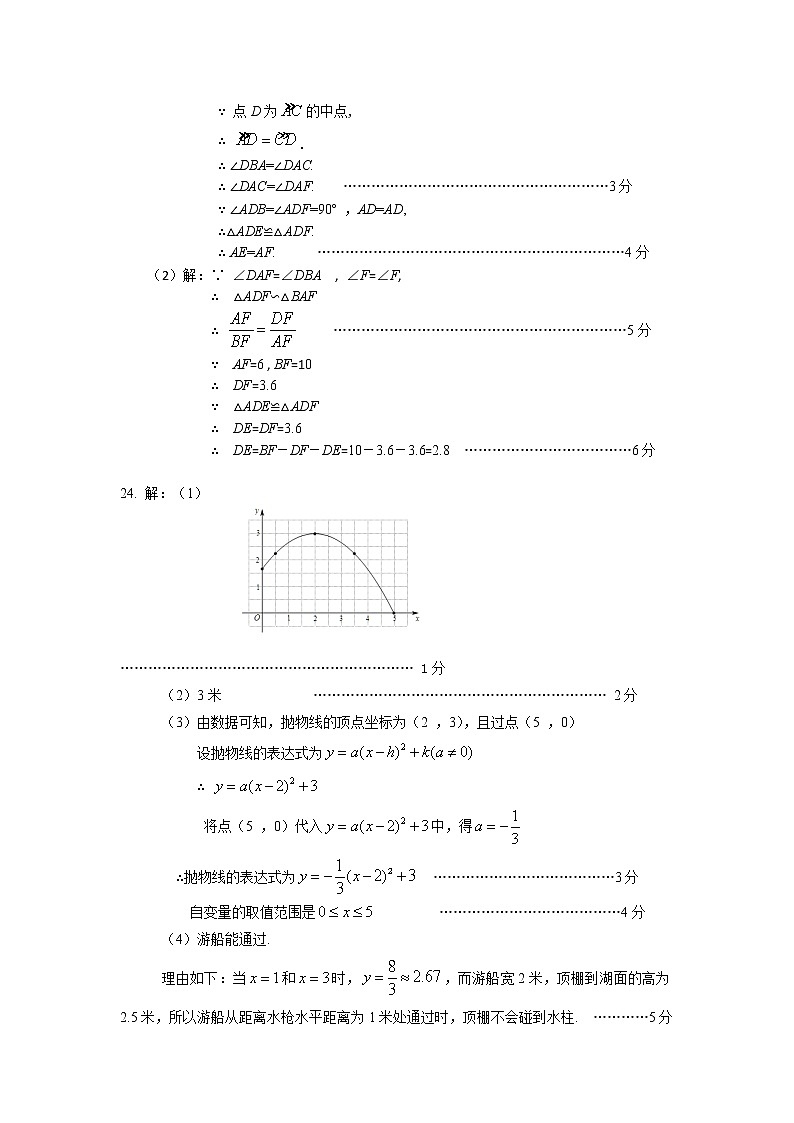
24. 解：（1）

                     ……………………………………………………… 1分

（2）3米             ……………………………………………………… 2分  

（3）由数据可知，抛物线的顶点坐标为（2 ，3），且过点（5 ，0）

     设抛物线的表达式为

     ∴

      将点（5 ，0）代入中，得

    ∴抛物线的表达式为  …………………………………3分

    自变量的取值范围是         …………………………………4分

（4）游船能通过.

理由如下：当和时，，而游船宽2米，顶棚到湖面的高为2.5米，所以游船从距离水枪水平距离为1米处通过时，顶棚不会碰到水柱.  …………5分

25.  解：（1）补全频数分布直方图如下            

                  ……………………………………………………… 1分

表中m的值为82   ……………………………………………………… 2分

         （2）此次七年级测试成绩达到优秀的学生为（人）

                                              ……………………………………3分

抽取八年级20名学生成绩的优秀率为

              此次八年级测试成绩达到优秀的学生为 （人）…… 4分

         （3）八年级的学生成绩较好.

理由是: 抽取的八年级20名学生的平均成绩为82，高于七年级, 两个年级的中位数接近，且八年级的学生成绩的方差小.    ………… 5分

26.  解：（1）法一∵令， 

                ∴，                                           

                ∴抛物线过点（0，），     ………………………………  1分

                ∵点在抛物线上

  ∴点（0，）和点是 抛物线上的对称点          

   ∴对称轴为.         ……………………………… 2分

        法二  ∵点在抛物线上           

∴

∴

∴对称轴为

（2）大小关系为 ，    ……………………………… 3分

理由如下 ：

∵对称轴是直线，，

            ∴点（，），（，）在对称轴的左侧，

             点（，）在对称轴的右侧， ………………… 4分

            设点（，）关于对称轴的对称点为（ ，）

           ∴

           ∴

           ∴点（，）关于对称轴的对称点为（，）

           ∵，

           ∴，                                  

           ，                               

                               …………………………   5分 

           ∵，

            ∴.                  …………………………   6分   

27.  

（1）证法一：∵EF垂直平分CD，

∴ED＝EC，FC＝FD．………………………………………………1分

又∵EF＝EF，

∴△ECF≌△EDF．   ………………………………………………2分

∴∠EDF＝∠ACB．

∵∠ACB＝90°，

∴∠EDF＝90°．   ………………………………………………3分

证法二：∵EF垂直平分CD，

∴ED＝EC，FC＝FD．  ………………………………………………1分

∴∠ECD＝∠EDC，∠FCD＝∠FDC．      ………………………2分

∴∠EDF＝∠EDC＋∠FDC＝∠ECD＋∠FCD＝∠ACB＝90°．……3分

（2）解：AE 2＋BF 2＝EF 2．     ……………………………………………………4分

延长FD至G，使DG＝DF，连接AG、EG．

∵AD＝BD，∠ADG＝∠BDF，DG＝DF，

∴△ADG≌△BDF．…………………………………………………5分

∴AG＝BF，∠DAG＝∠B．

∴AG∥BC，

∴∠EAG＝180°－∠ACB＝90°．

∴AE 2＋AG 2＝EG 2．  ………………………………………………6分

∵∠EDF＝90°，DG＝DF，

∴ED垂直平分FG．

∴EF＝EG．

∴AE 2＋BF 2＝EF 2．   ………………………………………………7分

28. 解:

  （1）B1C1，B2C2.    ………………………………………………2分

（2）如图，DE是BC的以直线l为轴的⊙O的“关联线段”，则△ADE是边长为a的等边三角形，此时，显然有DF=EF=，因此AF=，在Rt△ODF中，OD=2，DF=，OF=，根据勾股定理，可以得出，求解得到，舍去负值，得到.    …………………………………4分

如图 ，GH是BC的以直线l为轴的⊙O的“关联线段”，则△AGH是边长为a的等边三角形，此时，显然有GK=HK=，因此AK=，在Rt△OGK中，OG=2，GK=，OK=，根据勾股定理，可以得出，求解得到，舍去负值，得到.

综上，.    ………………………………………………5分

（3）或.     …………………………………………7分