基础知识重点、考点选择题专练--2022年初中数学中考备考二轮专题复习（一）

基础知识重点考点选择题专练（一）

一、单选题

1．抛物线y＝（x﹣1）2﹣2的顶点坐标为（       ）

A．（1，2） B．（1，﹣2） C．（﹣1，2） D．（﹣1，﹣2）

2．在平面直角坐标系中，点关于轴对称的点的坐标为（       ）

A． B． C． D．

3．某小组英语听力口语考试的分数依次为：25，29，27，25，22，30，26，这组数据的中位数是（       ）

A．27 B．26 C．25.5 D．25

4．﹣3的相反数是（　　）

A．3 B．±3 C． D．﹣

5．在－5，－2，0，1四个数中，比－3小的数是（       ）

A．1 B．－2 C．0 D．－5

6．已知2x＝3y（y≠0），则下面结论成立的是（             ）

A． B． C． D．

7．下列运算结果正确的是（       ）

A． B． C． D．

8．如图，小慧的眼睛离地面的距离为，她用三角尺测量广场上的旗杆高度，仰角恰与三角板角的边重合，量得小慧与旗杆之间的距离为，则旗杆的高度（单位：）为（       ）

A．6.6 B．11.6 C． D．

9．北京2022年冬奥会一共有超过1.9万名赛会志愿者，还有20余万人次的城市志愿者，他们是温暖这个冬天的雪花，他们把自己的志愿化成一道冬日的光，凝聚成温暖世界的力量．将20万用科学记数法表示应为（　　）

A．20×104 B．2×104 C．2×105 D．0.2×106

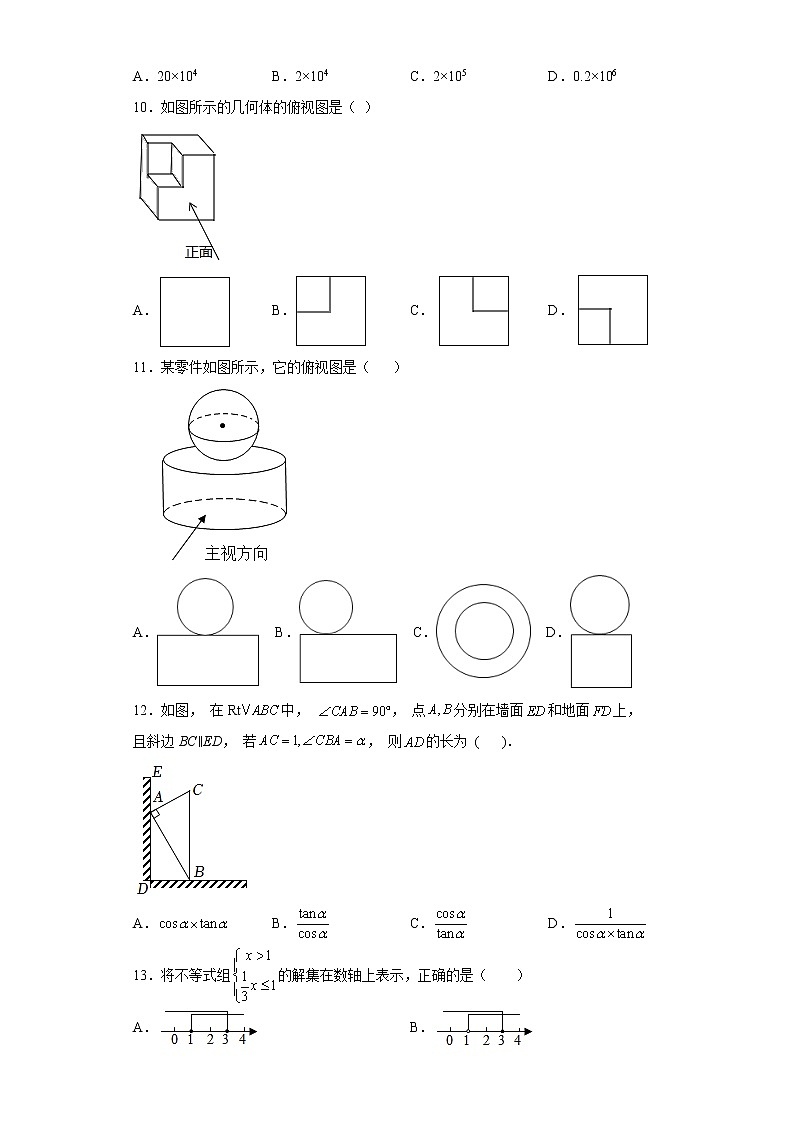
10．如图所示的几何体的俯视图是（ ）

A． B． C． D．

11．某零件如图所示，它的俯视图是（       ）

A．  B．  C．  D．

12．如图， 在Rt中， ， 点分别在墙面和地面上， 且斜边BC∥ED， 若， 则的长为 (       )．

A． B． C． D．

13．将不等式组的解集在数轴上表示，正确的是（　　）

A． B．

C． D．

14．下列运算正确的是（       ）

A． B． C． D．

15．若，那么（       ）

A．1 B．-1 C．-3 D．-5

16．方程组的解是（       ）

A． B． C． D．

17．如图，⊙O中，半径OC＝2，弦AB垂直平分OC，则AB的长是（　　）

A．3 B．4 C．2 D．4

18．下列运算正确的是（　　）

A． B．

C． D．

19．估计的值在（       ）

A．4到5之间 B．5到6之间 C．6到7之间 D．7到8之间

20．一次函数与二次函数在同一平面直角坐标系中的图象可能是（       ）

A． B．

C． D．

21．把抛物线y=-2x2向上平移1个单位，再向右平移1个单位，得到的抛物线是（     ）

A． B．

C． D．

22．如图，在正方形ABCD中，AB＝3，点E，F分别在边AB，CD上，∠EFD＝60°．若将四边形EBCF沿EF折叠，点B′恰好落在AD边上，则BE的长度为（       ）

A．1 B． C． D．2

23．一个数的相反数是5，则这个数是（　　）

A．5 B．﹣5 C． D．

24．如图，在⊙O中，点A在上，∠ABO＝50°，∠BAC＝110°，则∠ACO＝（　　）

A．80° B．70° C．60° D．55°

25．如图，菱形OABC的边OA在x轴上，点B坐标为（9，3），分别以点B、C为圆心，以大于BC的长为半径画弧，两弧交于点D、E，作直线DE，交x轴于点F，则点F的坐标是（       ）

A．（7.5，0） B．（6.5，0） C．（7，0） D．（8，0）

26．某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后卸完物品再另装货物共用45分钟，立即按原路以另一速度匀速返回，直至与货车相遇．已知货车的速度为60千米/时，两车之间的距离（千米）与货车行驶时间（小时）之间的函数图象如图所示，现有以下4个结论：

①快递车从甲地到乙地的速度为80千米/时；

②甲、乙两地之间的距离为120千米；

③图中点的坐标为；

④快递车从乙地返回时的速度为90千米/时．

以上4个结论中正确的是（     ）

A．①③④ B．①②④ C．②③④ D．③④

27．如图，矩形ABCD中，AD=2，AB=，对角线AC上有一点G（异于A，C），连接 DG，将△AGD绕点A 逆时针旋转60°得到△AEF，则BF的长为（     ）

A． B．2 C． D．2

28．如图，某大楼DE楼顶挂着“众志成城，抗击疫情”的大型宣传牌，为了测量宣传牌的高度CD，小江从楼底点E向前行走30米到达点A，在A处测得宣传牌下端D的仰角为60°．小江再沿斜坡AB行走26米到达点B，在点B测得宣传牌的上端C的仰角为43°，已知斜坡AB的坡度i＝1：2.4，点A、B、C、D、E在同一平面内，CD⊥AE，宣传牌CD的高度约为（　　）（参考数据：sin43°≈0.68，cos43°≈0.73，tan43°≈0.93，≈1.73）

A．8.3米 B．8.5米 C．8.7米 D．8.9米

29．已知关于x的分式方程无解，且关于y的不等式组有且只有三个偶数解，则符合条件的整数m有（　　）个．

A．0 B．1 C．2 D．3

30．古希腊数学家帕普斯利用反比例函数的图象和性质解决了三等分角问题，其方法如下：如图，在直角坐标系中，锐角的边OB在x轴正半轴上，边OA与的图象交于点A，以A为圆心，2OA为半径作圆弧交函数图象于点C，取AC的中点P，则．若，则k的值为（       ）

A． B． C． D．

1．B

【详解】

解：抛物线y＝（x﹣1）2﹣2的顶点坐标是（1，-2）．

2．D

【详解】

点关于轴对称的点的坐标为（3，-2），

3．B

【详解】

将这组数据从小到大重新排列为22，25，25，26，27，29，30，

∴这组数据的中位数为26，

4．A

【详解】

解：﹣3的相反数是3，

5．D

【详解】

解：∵|−5|=5，|−3|=3，

∴比−3小的数是：−5，

6．A

【详解】

A： 可以推出：2x＝3y，本选项正确；

B ：可以推出：xy＝6；本选项错误；

C：   可以推出：3x＝2y；本选项错误；

D：   可以推出：3x＝2y；本选项错误；

7．D

【详解】

解：A. ，原选项不正确，不符合题意；

B. ，原选项不正确，不符合题意；

C. ，原选项不正确，不符合题意；

D. ，原选项正确，符合题意；

8．D

【详解】

根据题意可知米，．

∵，

∴在中，米．

∴米．

9．C

【详解】

20万=200000，故20万用科学计数法可表示为：．

10．D

【详解】

解：从上面看是一个大正方形，大正方形内部的左下角是一个小正方形，

故选D．

11．C

【详解】

解：由题可知，从上面看零件是由两个同心圆组成的图形，故C正确．

12．C

【详解】

由题意得，

，

，

，

在

13．B

【详解】

解不等式x≤1，得：x≤3，

∴不等式组的解集为1＜x≤3，

∴不等式组的解集在数轴上表示出来如图所示：

．

14．A

【详解】

解：A、a2⋅a3=a5，故此选项符合题意；

B、a6÷a2=a4，故此选项不符合题意；

C、6a−2a=4a，故此选项不符合题意；

D、(−ab3)2=a2b6，故此选项不符合题意，

15．D

【详解】

解： ，

且，

解得，，

，

16．D

【详解】

解：

①+②得，

解得，

把代入①得，

解得，

所以，方程组的解为

17．C

【详解】

如图；连接OA

由圆的性质可知，OA=OC=2

∵AB垂直平分OC

∴OE=OC=×2=1

根据勾股定理，

由垂径定理可知AE=BE

∴

18．D

【详解】

不能化简，故A错误，不符合题意；

当a、b都为负数时，不成立，故B错误，不符合题意；

，故C错误，不符合题意；

，故D正确，符合题意；

19．B

【详解】

解：

=

=

∵

∴

∴

∴

20．B

【详解】

解：A、∵二次函数图象开口向上，对称轴在y轴右侧，抛物线与y轴的交点在x轴上方

∴a>0，b＜0，

∴一次函数图象应该过第一、三、四象限，A错误；

B、∵二次函数图象开口向上，对称轴在y轴左侧，抛物线与y轴的交点在x轴上方

∴a>0，b>0，

∴一次函数图象应该过第一、二、三象限，B正确；

C、∵二次函数图象开口向下，对称轴在y轴右侧，抛物线与y轴的交点在x轴上方

∴a<0，b>0，

∴一次函数图象应该过第一、二、四象限，C错误；

D、∵二次函数图象开口向下，对称轴在y轴左侧，抛物线与y轴的交点在x轴上方

∴a＜0，b＜0，

∴一次函数图象应该过第二、三、四象限，D错误．

21．B

【详解】

抛物线向上平移1个单位，可得，再向右平移1个单位得到的抛物线是．

22．D

【详解】

解：∵四边形ABCD是正方形，

∴AB∥CD，∠A=90°，

∴∠EFD=∠BEF=60°，

∵将四边形EBCF沿EF折叠，点B'恰好落在AD边上，

∴∠BEF=∠FEB'=60°，BE=B'E，

∴∠AEB'=180°-∠BEF-∠FEB'=60°，

∴B'E=2AE，

设BE=x，则B'E=x，AE=3-x，

∴2（3-x）=x，

解得x=2．

23．B

【详解】

解：根据相反数的定义，则这个数的相反数是﹣5．

24．C

【详解】

如图，在⊙O上取一点D，连接CD，BD，四边形ABDC为圆内接四边形，

则∠D+∠BAC＝180°，

∵∠BAC＝110°，

∴∠D＝70°，

∴∠BOC＝2∠D＝140°，

∵∠ABO＝50°，

∴∠ACO＝360°﹣∠BOC﹣∠ABO﹣∠BAC＝360°﹣140°﹣50°﹣110°＝60°，

25．B

【详解】

如图，过点B作BH⊥x轴于点H，设OA＝AB＝x．

∵B（9，3），

∴BH＝3，OH＝9，AH＝9﹣x，

在Rt△ABH中，则有x2＝32+（9﹣x）2，

∴x＝5，

∴OA＝AB＝BC＝5，

∴A（5，0），

∴DE垂直平分线段BC，

∴FH＝BC＝2.5，

∴OF＝6.5，

∴F（6.5，0），

26．D

【详解】

解：①设快递车从甲地到乙地的速度为x千米//时，则

3(x−60)=120，

x=100，故①不正确；

②因为120千米是快递车到达乙地后两车之间的距离，不是甲、乙两地之间的距离，故②错误；

③因为快递车到达乙地后缷完物品再另装货物共用45分钟，

所以图中点B的横坐标为，

纵坐标为，故③正确；

④设快递车从乙地返回时的速度为y千米//时，则返回时与货车共同行驶的时间为小时，此时两车还相距75千米，由题意，得

，

解得y=90，故④正确．

故其中正确的是：③④，

27．A

【详解】

解：如图，过点F作FH⊥BA交BA的延长线于点H，则∠FHA=90°，

∵△AGD绕点A 逆时针旋转60°得到△AEF

∴∠FAD=60°，AF=AD=2，

∵ 四边形ABCD是矩形

∴ ∠BAD=90°

∴∠BAF=∠FAD+ ∠BAD=150°

∴∠FAH=180°－∠BAF=30°

在Rt△AFH中，FH=AF=1

由勾股定理得

AH=

在Rt△BFH中，FH=1，BH=AH+AB=2

由勾股定理得

BF=

故BF的长．

28．A

【详解】

解：过B作BF⊥AE，交EA的延长线于F，作BG⊥DE于G．

Rt△ABF中，i=tan∠BAF=＝，AB=26米，

∴BF=10（米），AF=24（米），

∴BG=AF+AE=54（米），

Rt△BGC中，∠CBG=43°，

∴CG=BG•tan43°≈54×0.93=50.22（米），

Rt△ADE中，∠DAE=60°，AE=30米，

∴DE=AE=30（米），

∴CD=CG+GE-DE=50.22+10-30≈8.3（米）．

29．C

【详解】

解：分式方程去分母得：mx+2x﹣12＝3x﹣6，

移项合并得：（m﹣1）x＝6，

当m﹣1＝0，即m＝1时，方程无解；

当m﹣1≠0，即m≠1时，解得：x＝ ，

由分式方程无解，得到＝2或＝6，

解得：m＝4或m＝2，

不等式组整理得：，即﹣8≤y＜m﹣4，

由不等式组有且只有三个偶数解，得到整数解为﹣8，﹣7，﹣6，﹣5，﹣4，﹣3，

可得﹣4＜m﹣4≤﹣2，即0＜m≤2，

则符合题意m的值为1、2．

30．B

【详解】

解：作AE⊥OB于E，AD∥OB，CD∥AE，交直线OB于Q，两平行线交于点D，作CF∥AD，交AE于F，则四边形AFCD是矩形；FD经过点P，

设点A、点C坐标分别为，，则D点坐标为，F点坐标为，

设OD解析式为，把代入得，，

解得，，OD解析式为，

把代入得，，

则点F在直线OD上，

∵，

∴，

∵四边形AFCD是矩形，AC的中点为P，

∴，

∴，，

∵EF∥DQ，

∴△OEF∽△OQD，

∴，即，，

∵F点坐标为，点A坐标分别，

∴，，

把代入得，，

解得：（负值舍去），

故选：B．