小学数学8 数学广角——数与形单元测试课时训练

这是一份小学数学8 数学广角——数与形单元测试课时训练，共10页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
人教版六年级数学上册《8.数学广角——数与形》单元测试2   一、单选题(总分：25分本大题共5小题，共25分)1.(本题5分)如图，小明用3根小棒搭成一个三角形，5根小棒搭成2个三角形，找这样搭5个三角形需要（　　）根小棒．A.10
B.11
C.122.(本题5分)按图中的规律接着画下去，第（5）个图形一共有（　　）个这样的圆点．
 A.20
B.21
C.23
D.263.(本题5分)在下图中，矩形方框内有（ ）个三角形
 A.12
B.13
C.16
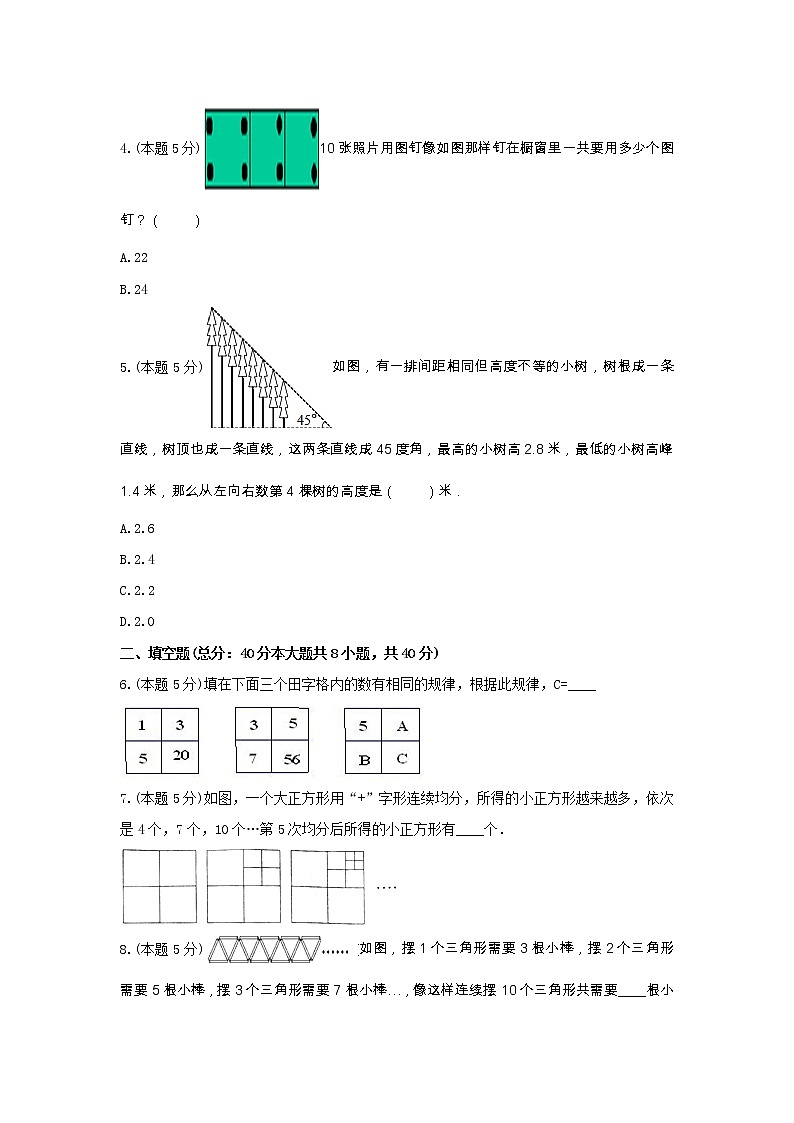
D.154.(本题5分)10张照片用图钉像如图那样钉在橱窗里一共要用多少个图钉？（　　）A.22
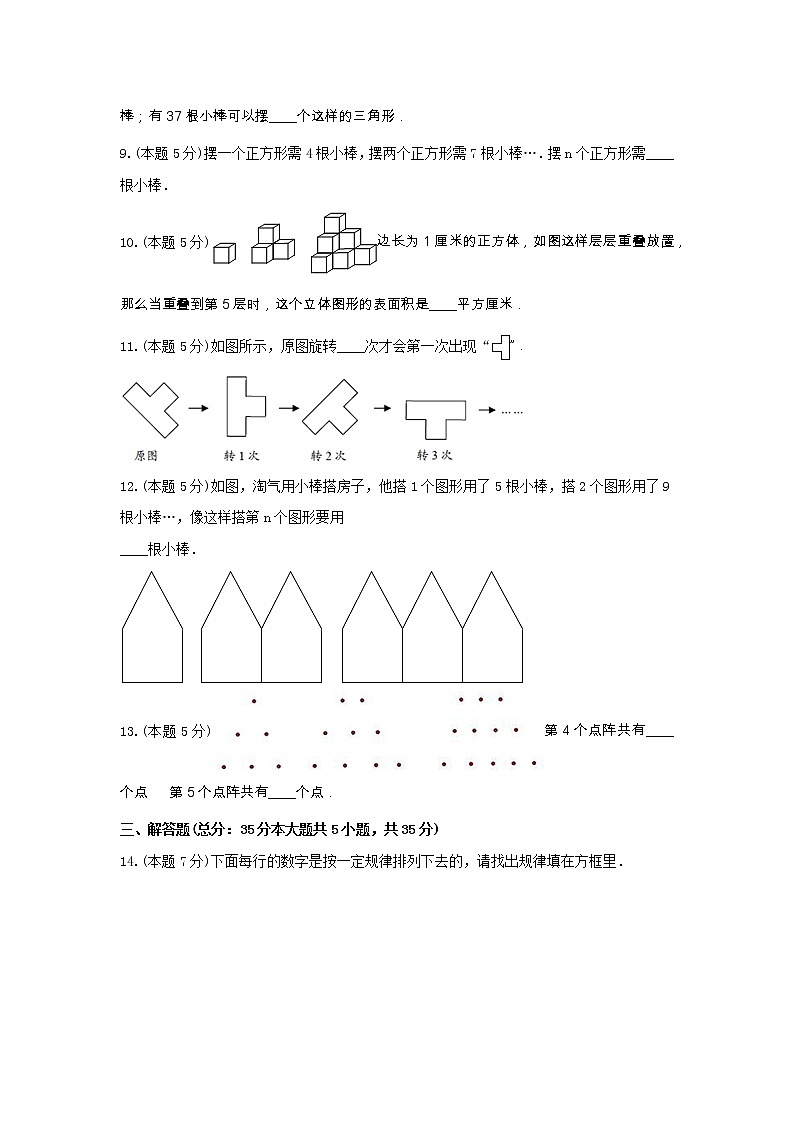
B.245.(本题5分)如图，有一排间距相同但高度不等的小树，树根成一条直线，树顶也成一条直线，这两条直线成45度角，最高的小树高2.8米，最低的小树高峰1.4米，那么从左向右数第4棵树的高度是（　　）米．A.2.6
B.2.4
C.2.2
D.2.0二、填空题(总分：40分本大题共8小题，共40分)6.(本题5分)填在下面三个田字格内的数有相同的规律，根据此规律，C=____
 7.(本题5分)如图，一个大正方形用“+”字形连续均分，所得的小正方形越来越多，依次是4个，7个，10个…第5次均分后所得的小正方形有____个．
 8.(本题5分)如图，摆1个三角形需要3根小棒，摆2个三角形需要5根小棒，摆3个三角形需要7根小棒…，像这样连续摆10个三角形共需要____根小棒；有37根小棒可以摆____个这样的三角形．9.(本题5分)摆一个正方形需4根小棒，摆两个正方形需7根小棒…．摆n个正方形需____根小棒．10.(本题5分)边长为1厘米的正方体，如图这样层层重叠放置，那么当重叠到第5层时，这个立体图形的表面积是____平方厘米．11.(本题5分)如图所示，原图旋转____次才会第一次出现“”．
 12.(本题5分)如图，淘气用小棒搭房子，他搭1个图形用了5根小棒，搭2个图形用了9根小棒…，像这样搭第n个图形要用
____根小棒．
 13.(本题5分)第4个点阵共有____个点   第5个点阵共有____个点．三、解答题(总分：35分本大题共5小题，共35分)14.(本题7分)下面每行的数字是按一定规律排列下去的，请找出规律填在方框里．
 15.(本题7分)如图的方式，2008根火柴棒能摆成多少个正方形？
 16.(本题7分)先画出第五个图形并填空．再想一想：后面的第10个方框里有____个点，第51个方框里有____个点．
 17.(本题7分)观察下面图中小圆圈的摆放规律，并按照这样的规律继续摆放，第15个图形中小圆圈的个数有多少个？
 18.(本题7分)观察各题中数的变化规律，再填数．
 
人教版六年级数学上册《8.数学广角——数与形》单元测试2参考答案与试题解析1.【答案】：B;【解析】：解：一个三角形需要3根火柴，
2个三角形需要3+2=5根火柴，
3个三角形需要3+2×2=7根火柴，
…
5个三角形需要3+2×（5-1）=11根火柴．
答：像这样摆5个同样的三角形需要11根小棒．
故选：B．2.【答案】：B;【解析】：解：根据分析可得：
第（5）个图形一共有圆点的个数是：
1+（5-1）×5
=1+20
=21（个）
故选：B．3.【答案】：C;【解析】：三角形的个数=图形个数×图形个数，那么第四个图形中三角形的个数就是4×4.4.【答案】：A;【解析】：解：10-1=9（张）
4+9×2=22（个）
故答案选：A．5.【答案】：C;【解析】：解：因为：
树根成一条直线，树顶也成一条直线
∠A=45°，最高的小树高2.8米，最低的小树高峰1.4米
所以AC=2.8米，AB=1.4米，BC=AC-AB=1.4米
又因为：这排树的间距相同
所以：
1.4÷7=0.2（米）
0.2×4+1.4
=0.8+1.4
=2.2（米）
答：那么从左向右数第4棵树的高度是2.2米．
故选：C．6.【答案】：108;【解析】：解：根据前两个图形的规律可知：
A=7，B=9，
所以：
C=9×（5+7）
=9×12
=108
故答案为：108．7.【答案】：16;【解析】：解：根据题干分析可得：第1次均分后得到的小正方形是3×1+1=4个
第2次均分后得到的小正方形是3×2+1=7个
第3次均分后得到的小正方形是3×3+1=10个
第4次均分后得到的小正方形是3×4+1=13个
则第n次均分后得到的小正方形是3n+1个；
那么第5次均分后得到的小正方形是
3n+1
=3×5+1
=16（个）
答：第5次均分后所得的小正方形有 16个．
故答案为：16．8.【答案】：21;18;【解析】：解：结合图形，发现：搭第n个图形，需要3+2（n-1）=2n+1（根）．
摆这样的10个小三角形，需要2×10+1=21根
有37根小棒，可以摆
2n+1=37
  2n=37-1
  2n=36
   n=18
答：摆这样的10个小三角形，需要21根小棒．有37根小棒，可以摆18个这样的小三角形．
故答案为：21；18．9.【答案】：3n+1;【解析】：解：第一个正方形由四根火柴摆成，以后加三根就可加一个正方形，摆n个正方形需要3n+1根小棒．
故答案为：3n+1．10.【答案】：90;【解析】：解：当重叠到5层时，
有1+3+6+10+15=35个正方体，
表面积为：
（1+2+3+4+5）×6=90（平方厘米）．
答：这个立体图形的表面积是90平方厘米．
故答案为：90．11.【答案】：6;【解析】：解：根据题干分析可得，第一次凸起指向右，第2次指向右下，第3次指向下，第4次指向左下，第5次指向左，则第6次就出现原图，
故答案为：6．12.【答案】：1+4n;【解析】：解：搭一间房用5根小棒，可以写成1+1×4；
2间房用9根小棒，可以写成1+2×4；
3间房用13根小棒，可以写成1+3×4；…
所以搭n间房子需要1+4n根小棒．
答：搭n间房子要用1+4n根小棒．
故答案为：1+4n．13.【答案】：15;18;【解析】：解：如图把每幅图中的点进行如下划分，则第一幅图中的点数为：3+1×3；第二幅图中点数为：3+2×3；第三幅图中点数为：3+3×3，…
由此可得第n幅图中点数为：3+3n，
当n=4时，3+3×4=15（个），
当n=5时，3+3×5=18（个）；
答：第4个点阵中有15个点，第5点阵中有18个点．
故答案为：15；18．
 14.【答案】：解：如图：
;【解析】：观察图形可知，每一行的第一个数和最后一个数都是1，其它的数是上面一行中的相邻的两个数的和，由此计算即可填空．15.【答案】：解：根据题干分析可得：摆n个正方形需要4+3（n-1）=3n+1根火柴棒，
当3n+1=2008时，
    3n=2007
     n=669
答：2008根火柴棒能摆成669个正方形．;【解析】：观察图形可知，摆一个正方形需要4根火柴棒，以后每多摆一个，需要3根火柴棒，所以摆n个正方形需要4+3（n-1）=3n+1根火柴棒，据此即可解答问题．16.【答案】：37201;【解析】：解：第五个图形有1+4×4个点，如图：

因为第n个图中共有1+4（n-1）个点，
所以第10个图中有1+4×（10-1）=37个点，
则第51个图共有1+4×（51-1）=201个点．
答：后面的第10个方框里有 37个点，第51个方框里有 201个点．
故答案为：37；201．17.【答案】：解：根据图形分析可知：（用s表示图中小黑点的个数）
n=1时，s=1；
n=2时，s=3=2×1+1；
n=3时，s=7=3×2+1；
n=4时，s=13=4×3+1；
n=5时，s=21=5×4+1；
…；
第n个图中小黑点的个数为n（n-1）+1．
第15个图形中的小黑点个数是
15×（15-1）+1
=15×14+1
=210+1
=211．
答：第15个图形中小圆圈的个数有211个．;【解析】：经过对一组图形进行分析比较，找出规律，再经过计算得出第n个图形中小黑点的个数，进一步即可求解．18.【答案】：解：13+14-9=18
故答案为：
;【解析】：由题意可得：每个正方形中对角上的两个数的和分别相等，如5+14=9+10、7+16=11+12，据此即可解答问题．