福建省莆田市仙游县郊尾、枫亭七校教研小片区2020-2021学年七年级（下）第一次月考数学试卷（含解析）

福建省莆田市仙游县郊尾、枫亭七校教研小片区2020-2021学年七年级（下）第一次月考数学试卷

一、选择题（本大题共10小题，共40.0分）

1. 81的平方根是

A.  B.  C. 9 D.

2. 如图，点P到直线l的距离是
    

A. 线段PA的长度 B. 线段PB的长度 C. 线段PC的长度 D. 线段PD的长度

3. 实数，，，，中，无理数的个数有

A. 1个 B. 2个 C. 3个 D. 4个

4. 如图所示，下列说法正确的是

A. 和是内错角
B. 和是同位角
C. 和是同旁内角
D. 和是内错角
 

5. 如图，直线AB与CD相交于点O，，，则的度数为
    

A.  B.  C.  D.

6. 下列说法中不正确的个数为
   ①在同一平面内，两条直线的位置关系只有两种：相交和垂直．
   ②有且只有一条直线垂直于已知直线．
   ③如果两条直线都与第三条直线平行，那么这两条直线也互相平行．
   ④从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离．
   ⑤过一点，有且只有一条直线与已知直线平行．

A. 2个 B. 3个 C. 4个 D. 5个

7. 如图，是由经过平移后得到的，且B，E，C，F在同一直线上，则平移的距离是

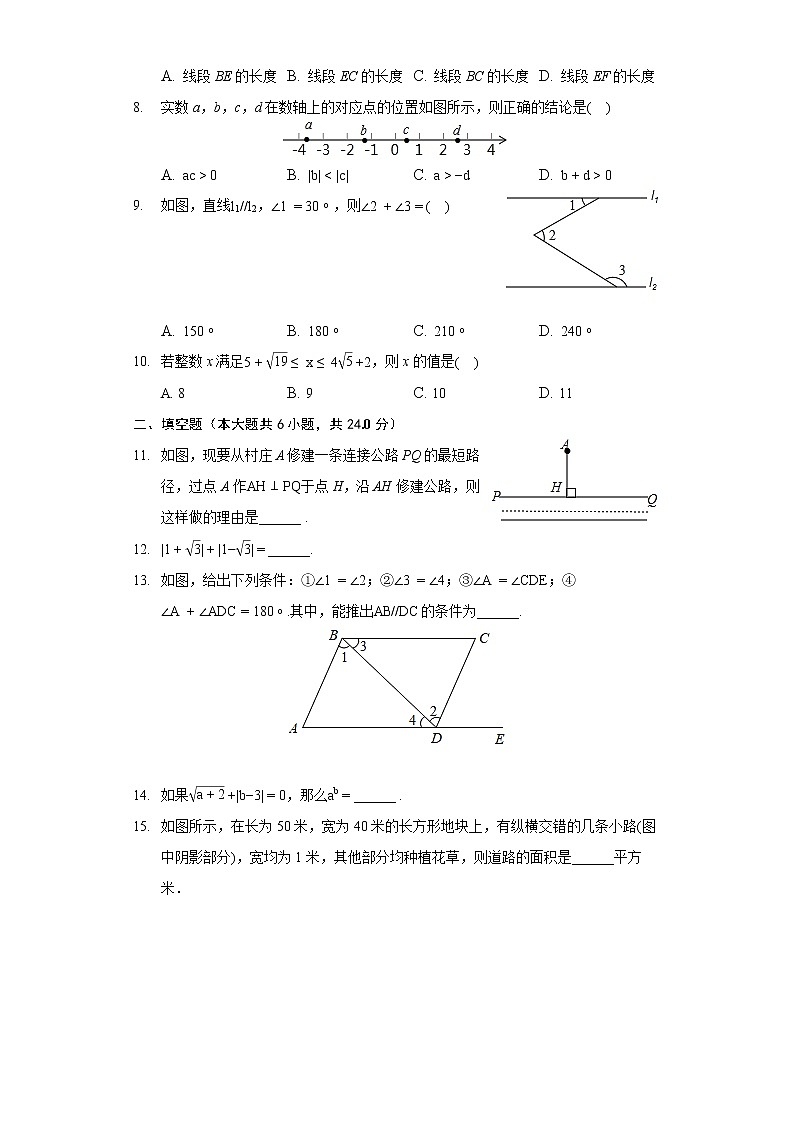
A. 线段BE的长度 B. 线段EC的长度 C. 线段BC的长度 D. 线段EF的长度

8. 实数a，b，c，d在数轴上的对应点的位置如图所示，则正确的结论是

A.  B.  C.  D.

9. 如图，直线，，则
   
   
    

A.  B.  C.  D.

10. 若整数x满足，则x的值是

1. 8 B. 9 C. 10 D. 11

二、填空题（本大题共6小题，共24.0分）

11. 如图，现要从村庄A修建一条连接公路PQ的最短路径，过点A作于点H，沿AH修建公路，则这样做的理由是______ .
12. ______.
13. 如图，给出下列条件：①；②；③；④其中，能推出的条件为______.

14. 如果，那么______ .
15. 如图所示，在长为50米，宽为40米的长方形地块上，有纵横交错的几条小路图中阴影部分，宽均为1米，其他部分均种植花草，则道路的面积是______平方米．

16. 观察下列各式：，，，…请利用你所发现的规律，计算…，其结果为______.

三、计算题（本大题共1小题，共14.0分）

17. 计算：；
    求x的值：

四、解答题（本大题共8小题，共72.0分）

18. 已知，如图所示，于D，于F，，说明AD是的角平分线请你完成下列说理过程在横线上填上适当的内容，在括号内写出说理依据
    理由：，已知
    ______，
    ______，
    ____________，
    ____________，
    又已知
    ____________，
    即AD是的角平分线．
    
    
    
    
    
    
     
19. 正数x的两个平方根分别是，
    求a的值；
    求这个数的立方根．
    
    
    
    
    
    
     
20. 如图，，AD平分，你能确定与的数量关系吗？请说明理由．
    
    
     

21. 如图，方格纸中每个小正方形的边长为1cm，点A、B、C均为格点．
    根据要求画图：
    ①过C点画直线；②过点C画AB的垂线，垂足为D点．
    图中线段______的长度表示点A到直线CD的距离；
    三角形ABC的面积=______
    
     

22. 阅读下面的文字，解答问题：大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部地写出来，于是小明用来表示的小数部分，因为的整数部分是1，将这个数减去其整数部分，差就是小数部分又例如：因为，即，所以的整数部分为2，小数部分为
    请解答：
    的整数部分是______，小数部分是______；
    如果的小数部分为a，的整数部分为b，求的值．
    
    
    
    
    
    
     
23. 如图，在四边形ABCD中，，连接BD，点E在BC边上，点F在DC边上，且
    求证：；
    若DB平分，，求的度数．
    
    
    
    
    
    
     
24. 如图所示，数轴上表示1和的对应点分别为A、B，点B关于点A的对称点是C，O为原点．
    分别求出线段AB、AC、OC长度；
    设C点表示的数为x，试求的值．
    
    
    
    
    
    
     
25. 如图，，BC平分，设为，点E是射线BC上的一个动点．
    若时，且，求的度数；
    若点E运动到上方，且满足，：：1，求a的值；
    若：，求的度数用含n和的代数式表示

答案和解析

1.【答案】D
 

【解析】解：，
的平方根是
故选：
根据平方根的定义进行解答即可．
本题考查了平方根的定义．解题的关键是掌握平方根的定义，即如果一个数的平方等于a，这个数就叫做a的平方根，也叫做a的二次方根．
 

2.【答案】C
 

【解析】解：点P到直线l的距离是线段PC的长度，
故选：
根据垂线段的性质“直线外和直线上所有点的连线中，垂线段最短”作答．
本题考查了点到直线的距离问题，关键是根据点到直线的距离的定义和垂线段的性质解答．
 

3.【答案】B
 

【解析】解：因为是整数，是有限小数，
所以、都是有理数；
因为，是循环小数，
所以是有理数；
因为，…，…，…都是无限不循环小数，
所以，都是无理数，
所以无理数的个数是2个：，
故选：
有理数能写成有限小数和无限循环小数，而无理数只能写成无限不循环小数，据此判断出无理数有哪些即可．
此题主要考查了无理数和有理数的特征和区别，要熟练掌握，解答此题的关键是要明确：有理数能写成有限小数和无限循环小数，而无理数只能写成无限不循环小数．
 

4.【答案】C
 

【解析】解：A、和是同旁内角，故错误；
B、和是不是同位角，故错误；
C、和是同旁内角，正确；
D、和不是同旁内角，故错误，
故选：
利用“三线八角”的定义分别判断后即可确定正确的选项．
本题考查了同位角、内错角及同旁内角的定义，解题的关键是了解三类角的定义，难度不大．
 

5.【答案】B
 

【解析】解：，
，
，
，
，
故选：
根据已知可得，再利用对顶角相等求出即可解答．
本题考查了垂线，对顶角与邻补角，根据题目的已知条件并结合图形分析是解题的关键．
 

6.【答案】C
 

【解析】解：因为在同一平面内，两条直线的位置关系只有两种：相交和平行，故①不正确；
因为过直线外一点有且只有一条直线垂直于已知直线．故②不正确；
如果两条直线都与第三条直线平行，那么这两条直线也互相平行．故③正确；
从直线外一点到这条直线的垂线段的长度，叫做这点到这条直线的距离．故④不正确；
⑤过直线外一点，有且只有一条直线与已知直线平行．故⑤不正确．
所以不正确的有①②④⑤四个．
故选：
根据在同一平面内，两条直线的位置关系，垂直的性质，平行线平行公理及推论，点到直线的距离等逐一进行判断即可．
本题考查了平行线的判定与性质、点到直线的距离、平行线、平行公理及推论，解决本题的关键是综合以上知识．
 

7.【答案】A
 

【解析】解：观察图形可知：是由沿BC向右移动BE的长度后得到的，
平移距离就是线段BE的长度．
故选：
根据平移的性质，结合图形可直接求解．
本题利用了平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．
 

8.【答案】D
 

【解析】解：根据数轴，，，，，
，，，故A错误；
，，，，故，故B错误；
，，，故，故C错误；
，，，故D正确．
故选：
首先根据数轴，写出a，b，c，d的取值范围，然后根据四个现象进行逐个判断
本题主要考查实数与数轴以及实数的大小比较，熟练实数相关知识点是解答此题的关键．
 

9.【答案】C
 

【解析】

【分析】
此题考查平行线的性质，关键是根据平行线的性质解答．
过点E作，利用平行线的性质解答即可．
【解答】
解：过点E作，

，，
，
，，
，
故选：  

10.【答案】C
 

【解析】解：，
，
，
，
，
，
，
，
整数x为
故选：
根据算术平方根的定义得到，，则，，然后把、9、10、11代入进行检验可得到时满足两个条件．
本题考查了估算无理数的大小：利用完全平方数和算术平方根对无理数的大小进行估算．也考查了算术平方根．
 

11.【答案】垂线段最短
 

【解析】解：从直线外一点到这条直线上各点所连线段中，垂线段最短，
过点A作于点H，这样做的理由是垂线段最短．
故答案为：垂线段最短．
根据垂线段的性质：垂线段最短可得结论．
本题主要考查了垂线段的性质，从直线外一点引一条直线的垂线，这点和垂足之间的线段叫做垂线段．
 

12.【答案】
 

【解析】解：
故答案为：
先依据各数的符号化去绝对值，再合并同类二次根式即可．
本题主要考查了实数的性质，正实数a的绝对值是它本身，负实数的绝对值是它的相反数，0的绝对值是
 

13.【答案】①③④
 

【解析】解：①，，故本选项符合题意；
②，，故本选项不符合题意；
③，，故本选项符合题意；
④，，故本选项符合题意．
故答案为：①③④．
直接根据平行线的判定定理对各小题进行逐一分析即可．
本题考查的是平行线的判定，掌握平行线的判定方法：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行是解题的关键．
 

14.【答案】
 

【解析】解：根据题意得，，，
解得，，
所以，
故答案为：
根据非负数的性质列式求出a、b的值，然后代入代数式进行计算即可得解．
本题主要考查了非负数的性质．根据非负数的性质：几个非负数的和为0时，这几个非负数都为0，求出a、b的值是解题的关键．
 

15.【答案】89
 

【解析】解：由题意可得，
道路的面积为：平方米
故答案为：
可以根据平移的性质，此小路相当于一条横向长为50米与一条纵向长为40米的小路，道路的面积=横纵小路的面积-小路交叉处的面积，计算即可．
本题考查了图形的平移的性质．解题的关键是掌握图形的平移的性质，要注意小路的交叉处算了两次，这是容易出错的地方．
 

16.【答案】
 

【解析】解：由题意可得，
…
…
…
…


，
故答案为：
根据题目中的式子，可以计算出所求式子的值，本题得以解决．
本题考查数字的变化类，解答本题的关键是明确题意，发现式子的特点，求出所求式子的值．
 

17.【答案】解：原式
；
根据平方根的定义得：
或，
或
 

【解析】根据立方根，有理数的乘方，算术平方根的定义计算即可；
根据平方根的定义解答．
本题考查了实数的运算，平方根，掌握一个正数的平方根有2个是解题的关键，不要漏解．
 

18.【答案】垂直的定义  同位角相等，两直线平行  两直线平行，同位角相等  两直线平行，内错角相等  等量代换
 

【解析】证明：，已知
，垂直的定义
同位角相等，两直线平行，
两直线平行，同位角相等，
两直线平行，内错角相等
又已知，
等量代换，
平分角平分线的定义
故答案为：垂直的定义，同位角相等，两直线平行，，两直线平行，同位角相等，，两直线平行，内错角相等，，等量代换．
先根据平行线的判定定理得出，由平新线的性质得出，，再由可得出，故可得出结论．
本题考查的是平行线的判定与性质，熟知平行线的判定定理是解答此题的关键．
 

19.【答案】解：正数x的两个平方根分别是和，
，
解得：，
即a的值是5；
，
，
这个正数的两个平方根是，
这个正数是
，
的立方根是
即这个数的立方根是
 

【解析】此题考查了立方根，平方根．解题的关键是掌握立方根、平方根的定义，注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．
根据一个正数有两个平方根，它们互为相反数，求出a的值；
根据a的值得出这个正数的两个平方根，即可得出这个正数，计算出的值，再根据立方根的定义即可解答．
 

20.【答案】解：与的数量关系是：
证明：平分
角平分线的定义
已知 
，两直线平行，同位角相等  
等量代换 
 

【解析】由角平分线的定义，平行线的性质可得
本题主要考查了角平分线的定义以及两直线平行，内错角相等、同位角相等这两个性质．
 

21.【答案】
 

【解析】解：如图，

①直线MN即为所求作的图形；
②AB的垂线CD即为所求；
图中线段AD的长度表示点A到直线CD的距离；
故答案为AD；
三角形ABC的面积为：


故答案为
①过C点画直线即可；
②过点C画AB的垂线，垂足为D点即可；
根据作图可得图中线段AD的长度表示点A到直线CD的距离；
根据网格即可求出三角形ABC的面积．
本题考查了作图-应用与设计作图、点到直线的距离、平行线的判定和性质、三角形的面积，解决本题的关键是准确画图．
 

22.【答案】
 

【解析】解：，
的整数部分是3，小数部分是，
故答案为：3，；

，，
，
，

根据解答即可；
根据得出a，根据得出b，再把a，b的值代入计算即可．
此题主要考查了估算无理数的大小，正确得出各无理数的小数部分是解题关键．
 

23.【答案】证明：如图，

已知，
两直线平行，内错角相等
，
等量代换
同位角相等，两直线平行

解：已知，
两直线平行，同旁内角互补
已知，

平分已知，


在中，三角形内角和定理，，

 

【解析】由知，结合得，据此即可得证；
由、知，再根据平分线定义及知，由三角形的内角和定理可得答案．
本题主要考查多边形的内角与外角、平行线的判定与性质，解题的关键是掌握平行线的判定与性质、三角形的内角和定理及角平分线的性质．
 

24.【答案】解：由数轴可得，，
点B关于点A的对称点是C，
，
；
答：，，；
由得，，
原式
 

【解析】用表示点B的数减去表示点A的数即可；根据对称性，；先表示点C的数，然后用表示点C的数减去表示点0的数即可；
先比较大小可得，然后根据绝对轴的性质进行计算即可得解．
本题考查了实数与数轴，绝对值以及两点间的距离的求解，求数轴上两点间的距离，用右边的数减去左边的数即可．
 

25.【答案】解：，，
，
平分，
，
，
又，
；
根据题意画图，如图1所示，
，：：1，
，
，
，
，
又平分，
，
；
①如图2所示，
，
，
平分，
，
，
又：，
：，
：，
解得；
②如图3所示，
，
，
平分，
，
，
又：，
：，
：，
解得
综上的度数为或
 

【解析】根据平行线的性质可得的度数，再根据角平分线的性质可得ABE的度数，应用三角形内角和计算的度数，由已知条件，可计算出的度数；
根据题意画出图形，先根据：：1可计算出的度数，由可计算出的度数，再根据平行线的性质和角平分线的性质，计算出的度数，即可得出结论；
根据题意可分两种情况，
①若点E运动到上方，根据平行线的性质由可计算出的度数，再根据角平分线的性质和平行线的性质，计算出的度数，再：，，列出等量关系求解即可等处结论；
②若点E运动到下方，根据平行线的性质由可计算出的度数，再根据角平分线的性质和平行线的性质，计算出的度数，再：，列出等量关系求解即可等处结论．
本题主要考查平行线的性质和角平分线的性质，两直线平行，同位角相等．两直线平行，同旁内角互补． 两直线平行，内错角相等．合理应用平行线的性质是解决本题的关键．