七年级下册第六章 实数综合与测试单元测试精练

这是一份七年级下册第六章 实数综合与测试单元测试精练，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
 第6章 实数 单元测试卷 一、选择题（本大题共10小题，共30分）在实数，，，，，，中无理数有A.  个 B.  个 C.  个 D.  个下列说法中错误的是A. 的平方根是 B. 是的一个平方根
C. 是的一个平方根 D. 的平方根是下列说法中，正确的是A. 任意两个有理数的和必是有理数
B. 任意有理数的绝对值必是正有理数
C. 任意两个无理数的和必是无理数
D. 任意有理数的平方必定大于或等于它本身如图，数轴上的点，，，，对应的数分别为，，，，，那么与实数对应的点在A. 线段上 B. 线段上 C. 线段上 D. 线段上已知，分别是的整数部分和小数部分，则A. ， B. ，
C. ， D. ，如图，每个小正方形的边长为，把阴影部分剪下来，用剪下来的阴影部分拼成一个正方形，那么新正方形的边长是A.
B.
C.
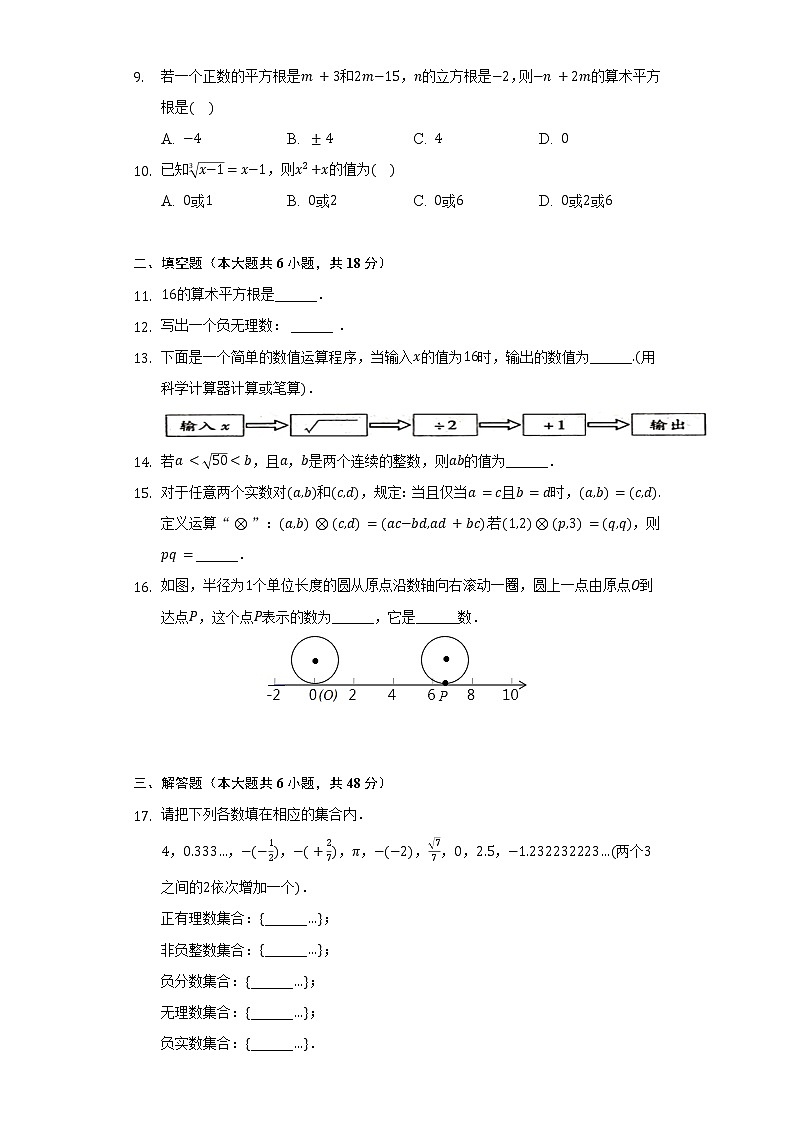
D. 若是的平方根，则A.  B.  C. 或 D. 和下列各式正确的是A.  B.  C.  D. 若一个正数的平方根是和，的立方根是，则的算术平方根是A.  B.  C.  D. 已知，则的值为A. 或 B. 或 C. 或 D. 或或 二、填空题（本大题共6小题，共18分）的算术平方根是______．写出一个负无理数： ______ ．下面是一个简单的数值运算程序，当输入的值为时，输出的数值为______用科学计算器计算或笔算．
 若，且，是两个连续的整数，则的值为______．对于任意两个实数对和，规定：当且仅当且时，定义运算“”：若，则______．如图，半径为个单位长度的圆从原点沿数轴向右滚动一圈，圆上一点由原点到达点，这个点表示的数为______，它是______数．
 三、解答题（本大题共6小题，共48分）请把下列各数填在相应的集合内．
，，，，，，，，，两个之间的依次增加一个．
正有理数集合：______；
非负整数集合：______；
负分数集合：______；
无理数集合：______；
负实数集合：______．






 计算：
．
．






 求下列各式中的值：
；
；
．






 已知，是有理数，且，满足等式，求的值．






 已知，，且．
如果的算术平方根为，求的值及的平方根．
如果，都是同一个数的平方根，求这个数．






 阅读下面的文字，解答问题：大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部写出来，而于是可用来表示的小数部分请解答下列问题：
的整数部分是______ ，小数部分是______ ；
如果的小数部分为，的整数部分为，求的值．







答案和解析 1.【答案】
 【解析】解：，，是整数，属于有理数；
是分数，属于有理数；
是有限小数，属于有理数；
无理数有，，共有个．
故选：．
无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
本题主要考查了无理数的定义，其中初中范围内学习的无理数有：，等；开方开不尽的数；以及像每两个之间依次多个，等有这样规律的数．
 2.【答案】
 【解析】解：、的平方根是，此选项正确；
B、的平方根是和，是的一个平方根，此选项正确；
C、由可知，是的一个平方根，此选项正确；
D、的平方根是，此选项错误；
故选：．
根据平方根的定义和性质逐一判断即可．
本题主要考查平方根，熟练掌握平方根得定义和性质是解题的关键．
 3.【答案】
 【解析】解：、任意两个有理数的和必是有理数，正确；
B、任意有理数的绝对值必是正有理数，错误，利用的绝对值等于；
C、任意两个无理数的和必是无理数，错误，利用；
D、任意有理数的平方必定大于或等于它本身，错误，例如．
故选：．
直接利用有理数的性质以及无理数的性质分别分析得出答案．
此题主要考查了实数运算，正确掌握相关性质是解题关键．
 4.【答案】
 【解析】解：，
，
那么与实数对应的点在线段上，
故选：．
先估算的大小，再确定的大小，可得结论．
本题考查了两点间的距离，数轴，无理数大小的估算，正确的理解题意是解题的关键．
 5.【答案】
 【解析】解：，
，
，
，；
故选：．
先求出范围，再两边都乘以，再两边都加上，即可求出、；．
本题考查了估算无理数的大小和有理数的混合运算的应用，关键是根据学生的计算能力进行解答．
 6.【答案】
 【解析】【分析】
本题考查了不规则图形的面积的求解方法：割补法．本题中阴影部分可分割成一个小正方形和一个等腰梯形．
本题中阴影部分可分割成一个小正方形和一个等腰梯形，，即重新拼成的正方形的面积为，则此正方形的边长为．
【解答】
解：阴影部分由一个小正方形和一个等腰梯形组成，
，
新正方形的边长
新正方形的边长，
故选：．  7.【答案】
 【解析】解：是的平方根，
或，
或．
故选：．
利用平方根的定义可得的值，再根据立方根的定义解答即可．
本题考查立方根、平方很，解答本题的关键掌握它们各自的含义．
 8.【答案】
 【解析】解：，故选项A错误，
，故选项B错误，
已经是最简的三次根式，故选项C错误，
，故选项D正确，
故选：．
根据各个选项中的式子可以计算出正确的结果，从而可以解答本题．
本题考查立方根、平方根、算术平方根，解答本题的关键是明确它们各自的计算方法．
 9.【答案】
 【解析】解：一个正数的两个平方根分别是和，
，
解得：，
的立方根是，
，
把，代入，
所以的算术平方根是．
故选：．
首先根据平方根的定义，求出值，再根据立方根的定义求出，代入，求出这个值的算术平方根即可．
本题考查了平方根、算术平方根、立方根．解题的关键是掌握平方根、算术平方根、立方根的定义，能够利用定义求出、值，然后再求的算术平方根，特别是最终求值，是本题的易错点．题目整体较难，适合课后培优训练．
 10.【答案】
 【解析】解：，
或或，
解得或或，
的值为或或．
故选：．
根据立方根等于它表示的数有和解答即可．
本题考查了立方根，掌握立方根的定义是解答本题的关键．
 11.【答案】
 【解析】【分析】
此题主要考查了算术平方根的定义．一个正数的算术平方根就是其正的平方根．根据算术平方根的定义即可求出结果．
【解答】
解：，
．
故答案为：．  12.【答案】答案不唯一
 【解析】【分析】
此题主要考查了无理数的定义，其中初中范围内学习的无理数有：，等；开方开不尽的数；以及像，等有这样规律的数．
无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称，即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．
【解答】解：写出一个负无理数，
故答案为：答案不唯一．  13.【答案】
 【解析】解：解：由题图可得代数式为．
当时，原式．
故答案为：
当输入的值为时，，，．
此题考查了代数式求值，此类题要能正确表示出代数式，然后代值计算，解答本题的关键就是弄清楚题目给出的计算程序．
 14.【答案】
 【解析】解：，，其中、为两个连续的整数，
，，
．
故答案为：．
直接利用的取值范围得出，的值，进而得出答案．
此题主要考查了估算无理数的大小，正确得出，的值是解题关键．
 15.【答案】
 【解析】解：根据题中的新定义化简得：，，
解得：，，
则，
故答案为：．
已知等式利用已知的新定义化简，计算即可求出所求．
此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
 16.【答案】  无理
 【解析】解：半径为，
周长；
从原点出发向右走了个单位，
所以点表示的数是．
是无限不循环小数，
是无理数．
故答案为：，无理．
根据半径求出圆的周长，即可确定点表示的数，它是无理数．
本题考查了在数轴上表示无理数，求解圆的周长是本题的关键．
 17.【答案】，，，，  ，，   ，，两个之间的依次增加一个  ，两个之间的依次增加一个
 【解析】解：正有理数集合：，
非负整数集合：，
负分数集合：
无理数集合：两个之间的依次增加一个，
负实数集合：两个之间的依次增加一个，
故答案为：，，，，；
，，；
；
，，两个之间的依次增加一个；
，两个之间的依次增加一个．
根据实数的分类解答即可．
本题考查了实数，熟练掌握有理数、无理数，正实数、负实数的概念是解题的关键．
 18.【答案】解：

；


．
 【解析】先化简各式，然后再进行计算即可解答；
先化简各式，然后再进行计算即可解答．
本题考查了实数的运算，准确熟练地化简各式是解题的关键．
 19.【答案】解：，
；
，
，
，
；
，
，
或．
 【解析】根据立方根的定义解决此题；
根据立方根的定义解决此题；
根据平方根的定义解决此题．
本题主要考查平方根、立方根，熟练掌握平方根、立方根的定义是解决本题的关键．
 20.【答案】解：，是有理数，并且满足等式，
，
得：，
．
 【解析】直接利用已知等式得出关于，的等式，进而得出答案．
此题主要考查了实数运算，正确得出关于，的值是解题关键．
 21.【答案】解：的算术平方根是，
，
解得；
，

故的平方根．
，都是同一个数的平方根，且，

解得，
，
答：这个数是．
 【解析】根据平方运算，可得，根据解一元一次方程，可得答案；
根据同一个数的平方根相等或互为相反数，可得的值，根据平方运算，可得答案．
本题考查了平方根和算术平方根，解题的关键是注意一个正数的平方根有两个，以防漏掉．
 22.【答案】 
 【解析】解：，
，
的整数部分为，小数部分为，
故答案为：，；
，
，
的小数部分，
，
，
，
的整数部分为，
．
估算的近似值，即可得出的整数部分和小数部分；
求出、的值，再代入计算即可．
本题考查无理数的估算，掌握算术平方根的意义是正确估算的前提．