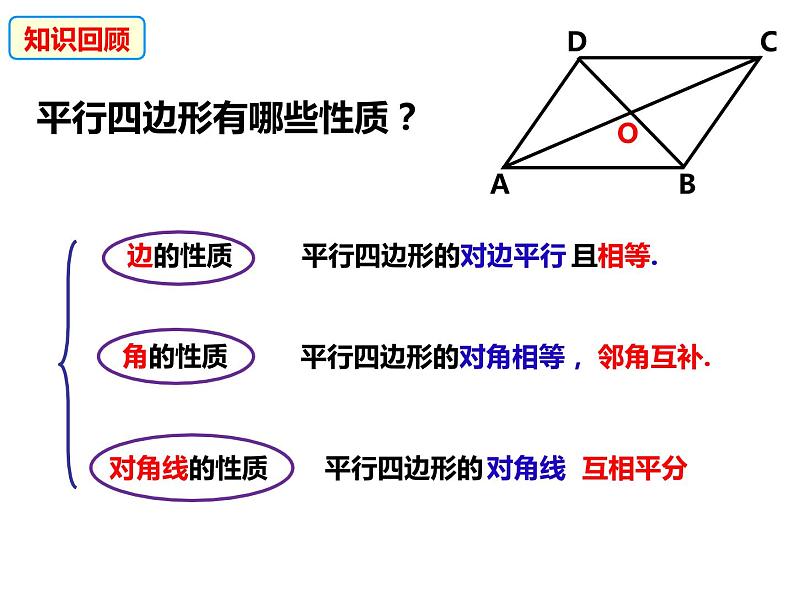
数学八年级下册19.3 矩形 菱形 正方形说课ppt课件

这是一份数学八年级下册19.3 矩形 菱形 正方形说课ppt课件，共41页。PPT课件主要包含了从边来判定，平行四边形的判定方法，知识回顾，从角来判定，从对角线来判定，判定定理1，判定定理2，本教材没有给出，判定定理3，连接三角形等内容，欢迎下载使用。

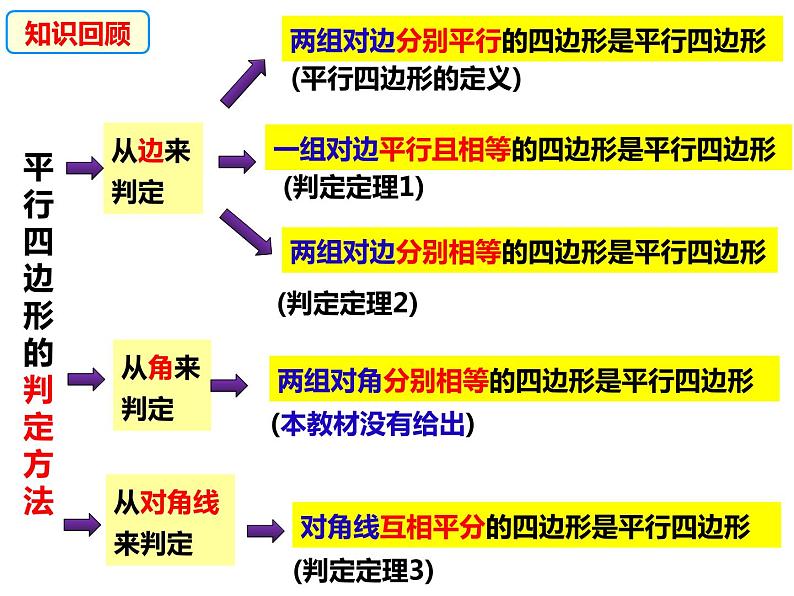
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
(平行四边形的定义)
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
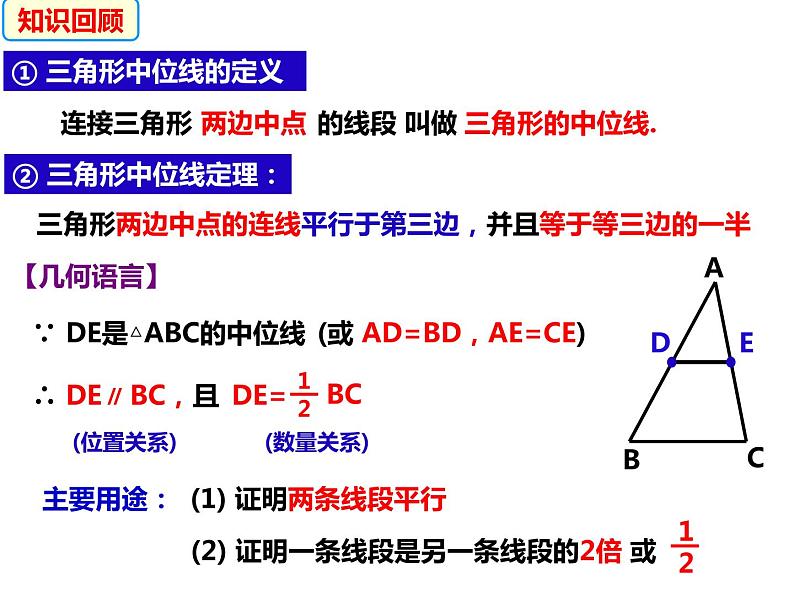
① 三角形中位线的定义
三角形两边中点的连线平行于第三边，并且等于等三边的一半
② 三角形中位线定理：
(2) 证明一条线段是另一条线段的2倍 或
∵ DE是△ABC的中位线
(或 AD=BD，AE=CE)
(1) 证明两条线段平行
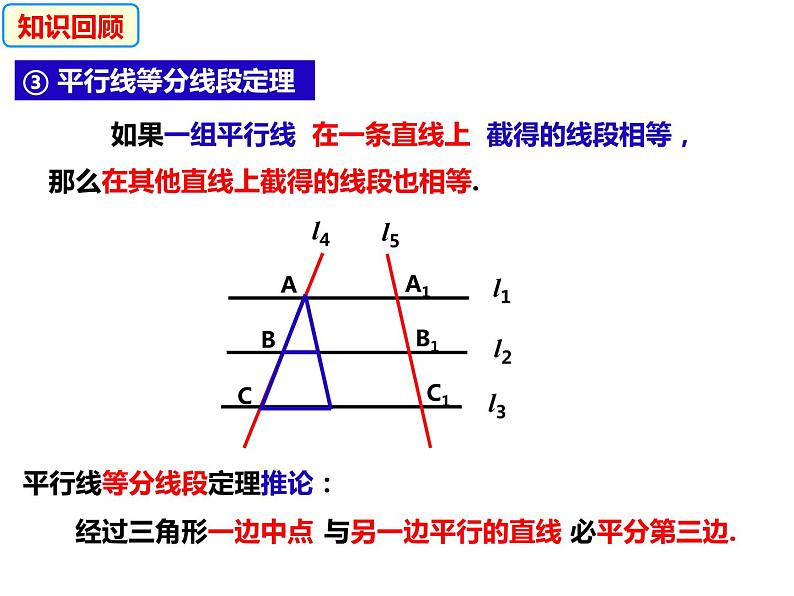
那么在其他直线上截得的线段也相等.
③ 平行线等分线段定理
平行线等分线段定理推论：
19.3.1 矩形及其性质
电脑、电视机的显示屏是什么形状？本书的封面是什么形状？
小学阶段我们称这些图形为长方形
思考：矩形跟我们前面学习的平行四边形有什么关系？
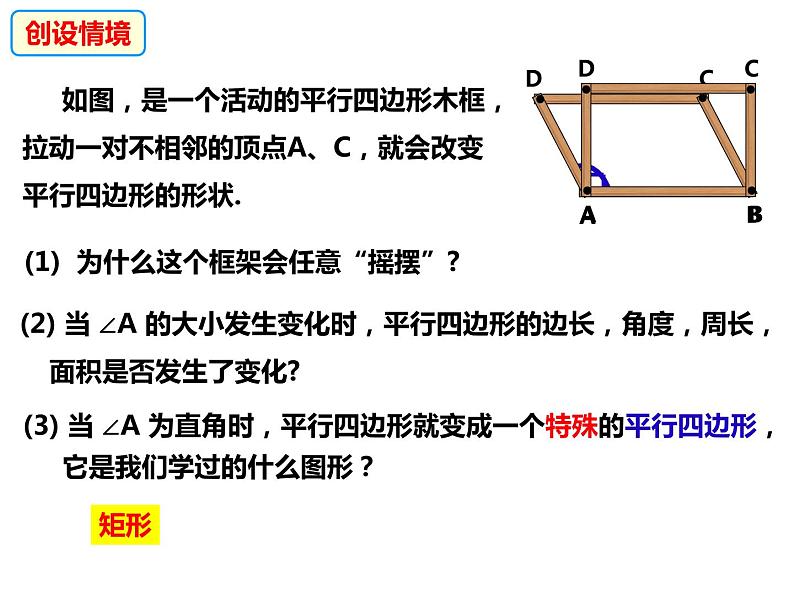
如图，是一个活动的平行四边形木框，拉动一对不相邻的顶点A、C，就会改变平行四边形的形状.
(2) 当 ∠A 的大小发生变化时，平行四边形的边长，角度，周长，面积是否发生了变化?
(3) 当 ∠A 为直角时，平行四边形就变成一个特殊的平行四边形， 它是我们学过的什么图形？
(1) 为什么这个框架会任意“摇摆”?
叫做 .
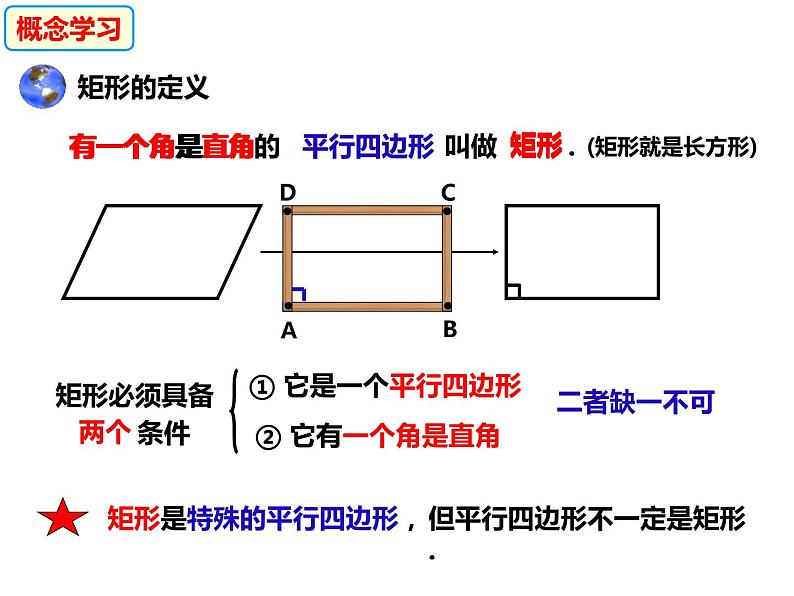
① 它是一个平行四边形
但平行四边形不一定是矩形.
有一个角是直角的平行四边形叫做矩形.
∵ 在 ABCD中，
∴  ABCD是矩形
∴ 四边形ABCD是平行四边形，
∵ 四边形ABCD是矩形
既是矩形的一种判定方法，
对应练习：下列哪个图形能够反映四边形、平行四边形、矩形的关系
因此矩形就具有平行四边形的一切性质.
我们知道矩形是一种特殊的平行四边形，
它的边、角和对角线还具有哪些特殊的性质呢？
思考：矩形除了具有一般平行四边形的性质外，
猜想1：矩形的四个角都是直角.
猜想2：矩形的对角线相等．
∵ 四边形 ABCD 是矩形
∴ ∠A=∠C=90°，
矩形的四个角都是直角.
∠A=∠B=∠C=∠D=90°
如图，四边形 ABCD 是矩形.
矩形必有一个角是直角，
∴ ∠B=180°-90°=90°
∴ ∠A=∠B=∠C=∠D=90°
即 矩形 ABCD 的四个角都是直角.
在矩形ABCD中，对角线AC和BD相交于点O.
∴ △ABC≌△DCB
∠ABC = ∠DCB = 90°
(矩形的四个角都是直角)
在△ABC和△DCB中
矩形的四个角都是直角．
矩形的两条对角线相等．
∵ 四边形ABCD是矩形∴ ∠ABC=∠BCD=∠CDA=∠DAB=90°
∵ 四边形ABCD是矩形∴ AC=BD
(矩形的两条对角线相等)
∵ 四边形ABCD是矩形∴ AC=BD，
∵ 四边形ABCD是矩形∴ AB CD，
1、矩形具有而一般平行四边形不具有的性质是 ( ) A.对角相等 B.对边相等 C.对角线相等 D.对角线互相平分
2、如图，矩形 ABCD 的对角线 AC、BD 相交于点 O，图中有多少个直角三角形？有多少个等腰三角形？
把矩形分成两个直角三角形，
将矩形分成四个等腰三角形.
矩形问题
直角三角形和等腰三角形中来解决
3、如图，EF过矩形ABCD对角线的交点O，且分别交AB、CD于E、F，那么阴影部分的面积是矩形ABCD面积的_________.
　　　　　　　　　　　　　
4、已知：如图，矩形 ABCD 的两条对角线相交于点 O，∠AOB=120°，AD=4cm. 求矩形对角线的长.
又∵ ∠AOB=120°
∵ 在Rt△ABD中，∠OBA=30°，AD=4cm.
5、已知矩形的一条对角线长8cm，两条对角线的夹角为60°，矩形相邻两边的长各为多少？
6、如图，在矩形 ABCD 中，∠BAD 的平分线交 BC 于点 E，O 为对角线 AC、BD 的交点，且 ∠CAE=15°(1) 求证：△AOB 为等边三角形；(2) 求 ∠AOE 度数．
如图，一张矩形纸片，画出两条对角线，沿着对角线 AC 剪去一半.
问题：在 Rt△ABC 中， BO 是一条怎样的线段？它的长度与斜边 AC 有什么关系？
直角三角形斜边上的中线等于斜边的一半.
OB = AC .
∴ 四边形ABCD是平行四边形
∵ ∠ABC=90°
∴ 平行四边形ABCD是矩形
∵ OA=OC， OD=OB
直角三角形斜边上的中线定理：
∵ 在Rt△ABC中，
(或 OB=OA=OC， )
7、如图，在△ABC中，∠ABC = 90°，BD 是斜边 AC 上的中线. (1) 若 BD=3cm，则AC =_____cm; (2) 若∠C = 30°，AB =5cm，则AC =_____cm, BD = _____cm. (3) 若∠C=35°，则 ∠ABD= .
8、如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=6cm，BC=8cm，则EF=______cm．
9、如图，DE 为 △ABC 的中位线，点 F 在 DE 上，且∠AFB=90°，若 AB=5，BC=8，则 EF 的长为 ．
10、如图，在△ABC中，AD是高，E、F分别是AB、AC的中点． (1)若AB＝10，AC＝8，求四边形AEDF的周长；
∵ 在Rt△ADB中，
∵ AD是△ABC的高
∴ ∠ADB=∠ADC=90°
又∵ 在Rt△ADC中，
AE＋DE＋DF＋AF
∴ 四边形AEDF的周长为
点E为斜边AB的中点，
点F为斜边AC的中点，
可联想直角三角形斜边上的中线的性质进行求解．
当已知条件含有线段的中点、
直角三角形的条件时，
(2) 求证：EF垂直平分AD.
∴ E、F在线段AD的垂直平分线上
DE＝AE，DF＝AF
(与线段两端距离相等的点在这条线段的垂直平分线上）
11、 如图，已知BD，CE是△ABC不同边上的高，点G，F分别是BC，DE的中点，试说明 GF⊥DE.
∵ 在Rt△BEC 中，
∵ BD，CE 分别为△ABC边上的高
∴ ∠BEC=∠BDC=90°
又∵ 在Rt△BDC中，
12、如图，在矩形ABCD中，AB=6，AD=8，P是AD上的动点，PE⊥AC，PF⊥BD于F，求PE+PF的值.
∴ ∠DAB=90°，
OA=OB=OC=OD
∴ S△AOD=S△DOC=S△AOB=S△BOC
= S矩形ABCD
= ×6×8=12
∵ 在Rt△ABD中，AB=6，AD=8
又∵ S△APO+S△DPO=S△AOD
13、如图，将矩形ABCD沿着直线BD折叠，使点C落在C′处，BC′交AD于点E，AD＝8，AB＝4，求△BED的面积．
解:∵ 四边形ABCD是矩形 ∴ AD∥ BC， ∴ ∠2＝∠3 由折叠知 ∠1＝∠2 ∴ ∠1＝∠3 ∴ BE＝DE 设BE＝DE＝x， ∵ 在Rt△ABE中，AB2＋AE2＝BE2 ∴ 42＋(8－x)2＝x2， 解得 x＝5 ∴ S△BED＝
矩形的折叠问题常与勾股定理结合考查
14、如图，点 P 是矩形 ABCD 的对角线 AC 上一点，过点 P 作EF∥BC，分别交 AB，CD 于 E、F，连接 PB、PD．若 AE=2，PF=8．则图中阴影部分的面积为（　　） A.10 B.12 C.16 D.18
15、如图，在矩形ABCD中，点M在DC上，AM=AB，且BN⊥AM，垂足为N．(1) 求证：△ABN≌△MAD；(2) 若AD=2，AN=4，求四边形BCMN的面积．
16、如图，在矩形 ABCD 中，AE⊥BD 于 E，∠DAE：∠BAE＝3:1，求 ∠BAO 和 ∠EAO 的度数．
∴ ∠DAE＝67.5°，
=67.5°-22.5°