





高中2.3 圆与圆的位置关系图文课件ppt
展开1.了解圆与圆的位置关系.2.掌握圆与圆的位置关系的判断方法.3.能用圆与圆的位置关系解决一些简单问题.
日食是一种天文现象,在民间称此现象为天狗食日.日食只在月球与太阳呈现合的状态时发生.日食分为日偏食、日全食、日环食、全环食.我们将月亮与太阳抽象为圆,观察到的这些圆在变化的过程中位置关系是怎样的?
前面我们运用直线的方程、圆的方程研究了直线与圆的位置关系,现在我们类比上述研究方法,运用圆的方程,通过定量计算研究圆与圆的位置关系.
一、圆与圆的位置关系的判断
1.代数法:设两圆的一般方程为
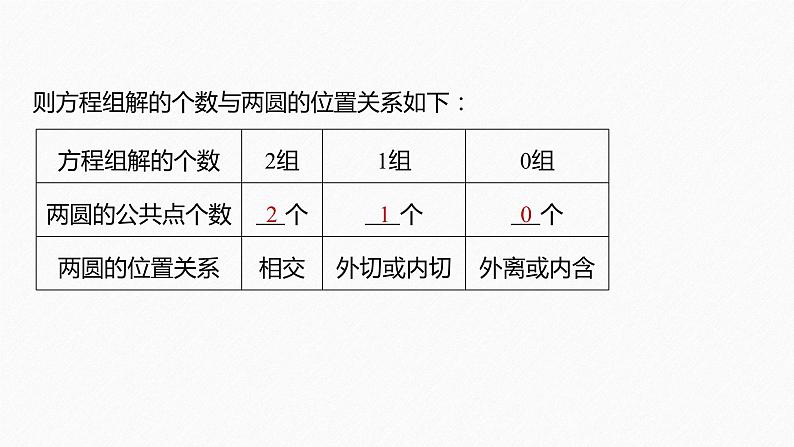
则方程组解的个数与两圆的位置关系如下:
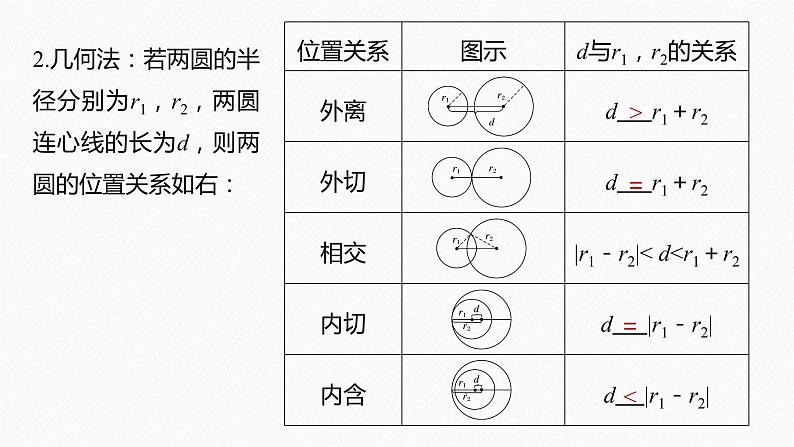
2.几何法:若两圆的半径分别为r1,r2,两圆连心线的长为d,则两圆的位置关系如右:
注意点:(1)利用代数法判断两圆位置关系时,当方程无解或有一解时,无法判断两圆的位置关系.(2)在判断两圆的位置关系时,优先使用几何法.
例1 当实数k为何值时,两圆C1:x2+y2+4x-6y+12=0,C2:x2+y2-2x-14y+k=0相交、相切、外离?
解 将两圆的一般方程化为标准方程,C1:(x+2)2+(y-3)2=1,C2:(x-1)2+(y-7)2=50-k.圆C1的圆心为C1(-2,3),半径长r1=1;
反思感悟 判断两圆的位置关系或利用两圆的位置关系求参数的取值范围有以下几个步骤(1)化成圆的标准方程,写出圆心和半径.(2)计算两圆圆心的距离d.(3)通过d,r1+r2,|r1-r2|的关系来判断两圆的位置关系或求参数的范围,必要时可借助于图形,数形结合.
跟踪训练1 已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x-2my+m2-3=0.(1)当m为何值时,圆C1与圆C2外切?
解 对于圆C1与圆C2的方程,经配方后,有C1:(x-m)2+(y+2)2=9.C2:(x+1)2+(y-m)2=4.∴两圆的圆心C1(m,-2),C2(-1,m),半径r1=3,r2=2,
若圆C1与圆C2相外切,则C1C2=r1+r2,
解得m=-5或m=2.
(2)当圆C1与圆C2内含时,求m的取值范围?
解 若圆C1与圆C2内含,则0≤C1C2<|r2-r1|=1,
问题1 圆与圆相切包含哪几种情况?
提示 内切和外切两种情况.
问题2 两圆相切可用什么方法求解?
提示 (1)几何法.利用圆心距d与两半径R,r之间的关系求得,d=R+r为外切,d=|R-r|为内切.(2)代数法.将两圆联立消去x或y得到关于y或x的一元二次方程,利用Δ=0求解.
处理两圆相切问题的两个步骤(1)定性,即必须准确把握是内切还是外切,若只是告诉相切,则必须分两圆内切还是外切两种情况讨论.(2)转化思想,即将两圆相切的问题转化为两圆的圆心距等于两圆半径之差的绝对值(内切时)或两圆半径之和(外切时).
例2 求半径为4,与圆(x-2)2+(y-1)2=9相切,且和直线y=0相切的圆的方程.
解 设所求圆的方程为(x-a)2+(y-b)2=16,由圆与直线y=0相切、半径为4,得圆心C的坐标为C1(a,4)或C2(a,-4).已知圆(x-2)2+(y-1)2=9的圆心A的坐标为(2,1),半径为3.由两圆相切,得CA=4+3=7或CA=4-3=1.①当圆心为C1(a,4)时,(a-2)2+(4-1)2=72或(a-2)2+(4-1)2=12(无解),
②当圆心为C2(a,-4)时,(a-2)2+(-4-1)2=72或(a-2)2+(-4-1)2=12(无解),
反思感悟 通过直线与圆,圆与圆的位置关系,建立数学模型,利用方程思想,解决求圆的方程问题.
解 已知圆的方程可化为(x-1)2+y2=1,则圆心为C(1,0),半径为1.设所求圆的方程为(x-a)2+(y-b)2=r2(r>0).
问题3 两圆相交时,如何求出公共弦所在的直线方程?
提示 将两个方程化成一般式,然后作差即可求得.
问题4 两圆公共弦长如何求得?
提示 将公共弦所在直线的方程与其中一个圆方程联立,
例3 已知圆C1:x2+y2+6x-4=0和圆C2:x2+y2+6y-28=0.(1)求两圆公共弦所在直线的方程及弦长;
解 设两圆交点为A(x1,y1),B(x2,y2),
①-②,得x-y+4=0.∵A,B两点的坐标都满足此方程,∴x-y+4=0即为两圆公共弦所在直线的方程.
(2)求经过两圆交点且圆心在直线x-y-4=0上的圆的方程.
得两圆的交点A(-1,3),B(-6,-2).设所求圆的圆心为(a,b),因为圆心在直线x-y-4=0上,故b=a-4.
即x2+y2-x+7y-32=0.
方法二 设所求圆的方程为x2+y2+6x-4+λ(x2+y2+6y-28)=0(λ≠-1),
解得λ=-7.故所求圆的方程为x2+y2-x+7y-32=0.
反思感悟 (1)求两圆的公共弦所在直线的方程的方法:将两圆方程相减即得两圆公共弦所在直线的方程,但必须注意只有当两圆方程中二次项系数相同时,才能如此求解,否则应先调整系数.(2)求两圆公共弦长的方法:一是联立两圆方程求出交点坐标,再用距离公式求解;二是先求出两圆公共弦所在的直线方程,再利用半径长、弦心距和弦长的一半构成的直角三角形求解.(3)已知圆C1:x2+y2+D1x+E1y+F1=0与圆C2:x2+y2+D2x+E2y+F2=0相交,则过两圆交点的圆的方程可设为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ≠-1).
跟踪训练3 圆心在直线x-y-4=0上,且经过圆x2+y2-4x-6=0与圆x2+y2-4y-6=0的交点的圆的方程为_____________________________________________.
(x-3)2+(y+1)2=16(或x2+y2-6x
所以圆x2+y2-4x-6=0与圆x2+y2-4y-6=0的交点分别为A(-1,-1),B(3,3),连接AB,则线段AB的垂直平分线的方程为y-1=-(x-1).
所以所求圆的圆心坐标为(3,-1),
所以所求圆的方程为(x-3)2+(y+1)2=16.方法二 同方法一求得A(-1,-1),B(3,3),设所求圆的方程为(x-a)2+(y-b)2=r2,
所以所求圆的方程为(x-3)2+(y+1)2=16.
方法三 设所求圆的方程为x2+y2-4x-6+λ(x2+y2-4y-6)=0,
所以所求圆的方程为x2+y2-6x+2y-6=0.
1.知识清单:(1)两圆的位置关系.(2)两圆的公共弦.(3)圆系方程.2.方法归纳:几何法、代数法.3.常见误区:将两圆内切和外切相混.
1.圆C1:x2+y2+2x+8y-8=0与圆C2:x2+y2-4x-4y-1=0的位置关系是A.外离 B.外切 C.相交 D.内含
解析 将圆的一般方程化为标准方程得C1:(x+1)2+(y+4)2=25,C2:(x-2)2+(y-2)2=9,∴C1(-1,-4),C2(2,2),r1=5,r2=3.
∴r1-r2<C1C2<r1+r2.因此两圆的位置关系为相交.故选C.
2.圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则AB的垂直平分线的方程是A.x+y+3=0 B.2x-y-5=0C.3x-y-9=0 D.4x-3y+7=0
解析 AB的垂直平分线过两圆的圆心,把圆心(2,-3)代入,即可排除A,B,D.故选C.
3.已知点P在圆O:x2+y2=1上运动,点Q在圆C:(x-3)2+y2=1上运动,则PQ的最小值为____.
解析 O(0,0),C(3,0),两圆半径均为1,
∴PQ的最小值为3-1-1=1.
4.已知圆C1:(x-1)2+(y-2)2=4,圆C2:x2+y2=1,则过圆C1与圆C2的两个交点且过原点O的圆的方程为__________________.
解析 设所求圆的方程为x2+y2-2x-4y+1+λ(x2+y2-1)=0(λ≠-1),把原点代入可得1-λ=0,所以λ=1,即可得过圆C1与圆C2的两个交点且过原点O的圆的方程为x2+y2-x-2y=0.
x2+y2-x-2y=0
1.圆x2+y2=2与圆x2+y2+2x-2y=0的位置关系是A.相交 B.内切C.外切 D.外离
解析 由题意得,圆x2+y2=2的圆心O1(0,0),圆x2+y2+2x-2y=0的圆心O2(-1,1),
故|r1-r2|
解析 圆C1的圆心为(1,0),半径为1;圆C2化为(x-4)2+(y+4)2=32-m,表示以(4,-4)为圆心,
由题意,两个圆相内切时,两圆的圆心距等于半径之差的绝对值,
综上,m的值为-4或16.
两个圆相外切,两圆的圆心距等于半径之和,
3.已知直线3x+4y+4=0与圆M:x2+y2-2ax=0(a>0)相切,则圆M和圆N:(x-1)2+ (y-1)2=1的位置关系是A.外离 B.外切C.相交 D.内切
解析 圆M的标准方程为(x-a)2+y2=a2(a>0),则圆心为(a,0),半径R=a,因为直线3x+4y+4=0与圆M:x2+y2-2ax=0(a>0)相切,
则圆M的圆心为(2,0),半径R=2,圆N的圆心为N(1,1),半径r=1,
因为R+r=3,R-r=1,所以R-r
解析 圆C1的圆心为(-1,-1),半径为1,圆C2的圆心为(3,4),半径为3,
5.圆C1:(x-1)2+y2=4与圆C2:(x+1)2+(y-3)2=9的相交弦所在的直线为l,则直线l被圆O:x2+y2=4截得的弦长为
解析 由圆C1与圆C2的方程相减得l:2x-3y+2=0.
6.(多选)下列圆中与圆C:x2+y2+2x-4y+1=0相切的是A.(x+2)2+(y+2)2=9 B.(x-2)2+(y+2)2=9C.(x-2)2+(y-2)2=25 D.(x-2)2+(y+2)2=49
解析 由圆C:x2+y2+2x-4y+1=0,可知圆心C的坐标为(-1,2),半径r=2.A项,圆心C1(-2,-2),半径r1=3.
∴两圆相交;B项,圆心C2(2,-2),半径r2=3,∵C2C=5=r+r2,∴两圆外切,满足条件;
C项,圆心C3(2,2),半径r3=5,∵C3C=3=r3-r,∴两圆内切;D项,圆心C4(2,-2),半径r4=7,∵C4C=5=r4-r,∴两圆内切.
7.经过直线x+y+1=0与圆x2+y2=2的交点,且过点(1,2)的圆的方程为______________________.
解析 由已知可设所求圆的方程为x2+y2-2+λ(x+y+1)=0,将(1,2)代入,
8.过两圆x2+y2-2y-4=0与x2+y2-4x+2y=0的交点,且圆心在直线l:2x+4y-1=0上的圆的方程是____________________.
解析 设圆的方程为x2+y2-4x+2y+λ(x2+y2-2y-4)=0(λ≠-1),则(1+λ)x2-4x+(1+λ)y2+(2-2λ)y-4λ=0,
x2+y2-3x+y-1=0
所以所求圆的方程为x2+y2-3x+y-1=0.
所以圆O2的圆心在直线y=x上,不妨设为(a,a),因为圆O2过点A(0,-4),所以圆O2与圆O1外切,
所以a=0,所以圆O2的方程为x2+y2=16.
10.已知两圆C1:x2+y2=4,C2:(x-1)2+(y-2)2=r2(r>0),直线l:x+2y=0.(1)当圆C1与圆C2相交且公共弦长为4时,求r的值;
解 由圆C1:x2+y2=4,知圆心C1(0,0),半径r1=2,又由圆C2:(x-1)2+(y-2)2=r2(r>0),可得x2+y2-2x-4y+5-r2=0,两式相减可得公共弦所在的直线方程为2x+4y-9+r2=0.因为圆C1与圆C2相交且公共弦长为4,所以此时相交弦过圆心C1(0,0),即r2=9(r>0),解得r=3.
(2)当r=1时,求经过圆C1与圆C2的交点且和直线l相切的圆的方程.
解 设过圆C1与圆C2的圆系方程为(x-1)2+(y-2)2-1+λ(x2+y2-4)=0(λ≠-1),即(1+λ)x2+(1+λ)·y2-2x-4y+4(1-λ)=0,
由圆心到直线x+2y=0的距离等于圆的半径,
故所求圆的方程为x2+y2-x-2y=0.
11.过点P(2,3)向圆C:x2+y2=1上作两条切线PA,PB,则弦AB所在的直线方程为A.2x-3y-1=0 B.2x+3y-1=0C.3x+2y-1=0 D.3x-2y-1=0
解析 因为PC垂直平分AB,故弦AB可以看作是以PC为直径的圆与圆x2+y2=1的公共弦,
根据两圆的公共弦的求法,
整理可得2x+3y-1=0.
12.(多选)圆O1:x2+y2-2x=0和圆O2:x2+y2+2x-4y=0的交点为A,B,则有A.公共弦AB所在直线的方程为x-y=0B.线段AB中垂线的方程为x+y-1=0
解析 对于A,由圆O1:x2+y2-2x=0与圆O2:x2+y2+2x-4y=0的交点为A,B,两式作差可得4x-4y=0,即公共弦AB所在直线的方程为x-y=0,故A正确;对于B,圆O1:x2+y2-2x=0的圆心为(1,0),又kAB=1,则线段AB中垂线的斜率为-1,即线段AB中垂线的方程为y-0=-1×(x-1),整理可得x+y-1=0,故B正确;
对于C,圆O1:x2+y2-2x=0,
对于D,P为圆O1上一动点,
13.已知两圆C1、C2和x轴正半轴、y轴正半轴及直线x+y=2都相切,则两圆圆心的距离C1C2=______.
解析 因为两圆C1,C2和x轴正半轴、y轴正半轴及直线x+y=2都相切,所以两圆圆心都在直线y=x上,设C1(a,a),则圆C1的方程为(x-a)2+(y-a)2=a2,设C2(b,b),则圆C2的方程为(x-b)2+(y-b)2=b2,因为两圆均与直线x+y-2=0相切,
14.在平面直角坐标系xOy中,已知圆C1 : x2 +y2=8与圆C2 : x2+y2+2x+y-a=0相交于A,B两点.若圆C1上存在点P,使得△ABP为等腰直角三角形,则实数a的值组成的集合为_____________________.
解析 由题意知,直线AB为2x+y+8-a=0,当∠PAB=90°或∠PBA=90°时,设C1到AB的距离为d,因为△ABP为等腰直角三角形,
当∠APB=90°时,AB经过圆心C1,则8-a=0,即a=8.
解析 设圆C1的半径为r=1,
16.已知圆C:x2+y2-6x-8y+21=0.(1)若直线l1过定点A(1,1),且与圆C相切,求l1的方程;
解 圆C:x2+y2-6x-8y+21=0化为标准方程为(x-3)2+(y-4)2=4,所以圆C的圆心为(3,4),半径为2.①若直线l1的斜率不存在,即直线为x=1,符合题意.②若直线l1的斜率存在,设直线l1的方程为y-1=k(x-1).即kx-y-k+1=0.由题意知,圆心(3,4)到已知直线l1的距离等于半径2,
综上,所求l1的方程为x=1或5x-12y+7=0.
高中数学苏教版 (2019)选择性必修第一册2.3 圆与圆的位置关系授课ppt课件: 这是一份高中数学苏教版 (2019)选择性必修第一册2.3 圆与圆的位置关系授课ppt课件,共22页。PPT课件主要包含了知识点4圆系方程等内容,欢迎下载使用。
高中数学人教A版 (2019)选择性必修 第一册第二章 直线和圆的方程2.5 直线与圆、圆与圆的位置图片课件ppt: 这是一份高中数学人教A版 (2019)选择性必修 第一册第二章 直线和圆的方程2.5 直线与圆、圆与圆的位置图片课件ppt,共51页。PPT课件主要包含了知识特训,能力特训等内容,欢迎下载使用。
苏教版 (2019)选择性必修第一册第2章 圆与方程2.3 圆与圆的位置关系授课课件ppt: 这是一份苏教版 (2019)选择性必修第一册第2章 圆与方程2.3 圆与圆的位置关系授课课件ppt,文件包含23圆与圆的位置关系pptx、23圆与圆的位置关系doc等2份课件配套教学资源,其中PPT共47页, 欢迎下载使用。













