苏教版 (2019)选择性必修第一册5.3 导数在研究函数中的应用教案配套课件ppt

这是一份苏教版 (2019)选择性必修第一册5.3 导数在研究函数中的应用教案配套课件ppt，共60页。PPT课件主要包含了学习目标，随堂演练，课时对点练，极值与最值的关系，求函数的最值，内容索引，提示如图，最大值，最小值，令f′x＝0等内容，欢迎下载使用。
1.理解最值的概念，了解其与函数极值的区别与联系.2.会求某闭区间上的最值并能解决生活中的最值问题.
同学们，上节课我们在群山之间穿梭，感受了每一个山峰与山谷的优美之处，而今天我们誓要寻找最高的山峰和最低的峡谷，我们既要有俯视一切的雄心和气概，拿出“会当凌绝顶，一览众山小”的气势，也要有仰望一切的谦虚和胸怀，更要有“可上九天揽月，可下五洋捉鳖”的勇气，这其实就是我们今天要探究的函数的最值.
三、用导数解决实际问题
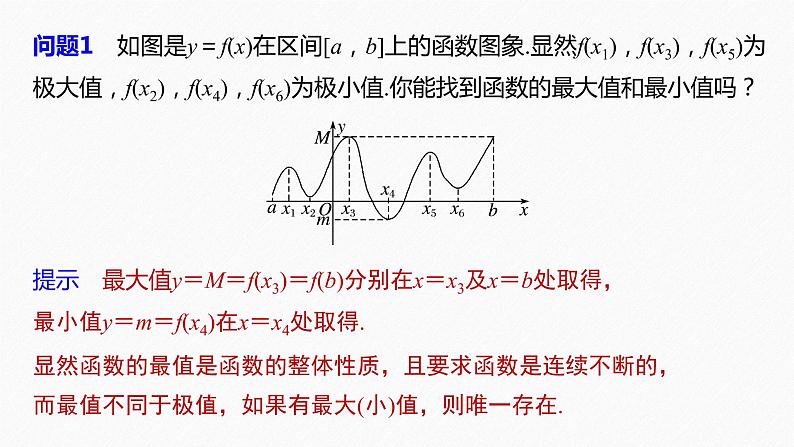
问题1　如图是y＝f(x)在区间[a，b]上的函数图象.显然f(x1)，f(x3)，f(x5)为极大值，f(x2)，f(x4)，f(x6)为极小值.你能找到函数的最大值和最小值吗？
提示　最大值y＝M＝f(x3)＝f(b)分别在x＝x3及x＝b处取得，最小值y＝m＝f(x4)在x＝x4处取得.显然函数的最值是函数的整体性质，且要求函数是连续不断的，而最值不同于极值，如果有最大(小)值，则唯一存在.
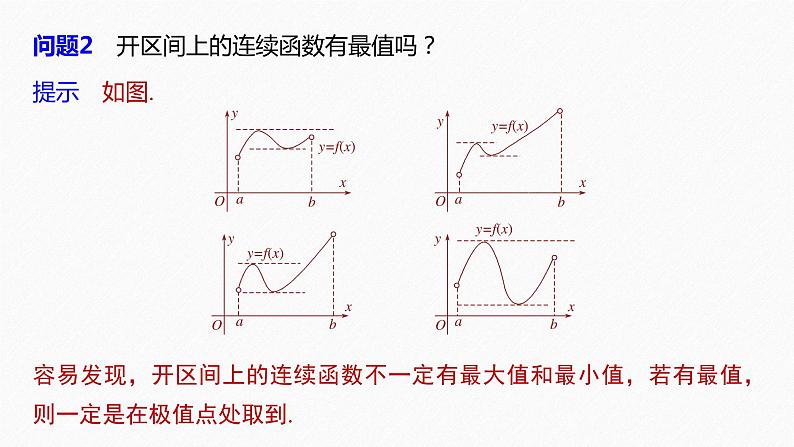
问题2　开区间上的连续函数有最值吗？
容易发现，开区间上的连续函数不一定有最大值和最小值，若有最值，则一定是在极值点处取到.
函数最值的定义(1)一般地，如果在区间[a，b]上函数y＝f(x)的图象是一条连续不断的曲线，那么它必有最大值和最小值.(2)如果在函数定义域I内存在x0，使得对任意x∈I，总有f(x)≤f(x0)，那么f(x0)为函数在定义域上的最大值；如果在函数定义域I内存在x0，使得对任意x∈I，总有f(x)≥f(x0)，那么f(x0)为函数在定义域内的最小值.注意点：(1)开区间不一定有最值，闭区间上的连续函数一定有最值；(2)函数f(x)在闭区间[a，b]上连续是f(x)在闭区间[a，b]上有最大值和最小值的充分不必要条件.
例1　如图是函数y＝f(x)在区间[a，b]上的图象，写出函数的极大值、极小值、最大值和最小值.
解　由题图可知，y＝f(x)在x1，x3处取得极小值，在x2处取得极大值，
最大值在b处取得，最大值为f(b).
反思感悟　最值与极值的区别与联系(1)极值是对某一点附近(即局部)而言，最值是对函数的定义区间的整体而言.(2)在函数的定义区间内，极大(小)值可能有多个，但最大(小)值只有一个(或者没有).(3)函数f(x)的极值点为定义域中的内点，而最值点可以是区间的端点.(4)对于可导函数，函数的最大(小)值必在极大(小)值点或区间端点处取得.
跟踪训练1　设f(x)是区间[a，b]上的连续函数，且在(a，b)内可导，则下列结论中正确的是A.f(x)的极值点一定是最值点B.f(x)的最值点一定是极值点C.f(x)在区间[a，b]上可能没有极值点D.f(x)在区间[a，b]上可能没有最值点
解析　根据函数的极值与最值的概念知，f(x)的极值点不一定是最值点，f(x)的最值点不一定是极值点.可能是区间的端点，连续可导函数在闭区间上一定有最值，所以选项A，B，D都不正确，若函数f(x)在区间[a，b]上单调，则函数f(x)在区间[a，b]上没有极值点，所以C正确.
求f(x)在区间[a，b]上的最大值与最小值的步骤：(1)求f(x)在区间(a，b)上的 ；(2)将(1)中求得的极值与f(a)，f(b) ，得到f(x)在区间[a，b]上的 与 .
例2　求下列函数的最值：(1)f(x)＝2x3－12x，x∈[－2,3]；
解　因为f(x)＝2x3－12x，x∈[－2,3]，
因为f(－2)＝8，f(3)＝18，
当x＝3时，f(x)取得最大值18.
因为f(0)＝1，f(2π)＝π＋1，
所以当x＝2π时，f(x)有最大值f(2π)＝π＋1，
反思感悟　求函数最值需注意的点(1)确定函数的定义域.(2)求出定义域内的每一个极值与最值.(3)比较所求的每一个极值与最值.(4)得出结论.
跟踪训练2　求下列函数的最值：(1)f(x)＝2x3－6x2＋3，x∈[－2,4]；
解　f′(x)＝6x2－12x＝6x(x－2).令f′(x)＝0，得x＝0或x＝2.又f(0)＝3，f(2)＝－5，f(4)＝35，f(－2)＝－37，∴当x＝4时，f(x)取最大值35.当x＝－2时，f(x)取最小值－37.即f(x)的最大值为35，最小值为－37.
当f′(x)＝0时，x＝2，当x变化时，f′(x)，f(x)的变化情况如表所示.
∴f(x)在(－∞，2)上是增函数，在(2，＋∞)上是减函数，
例3　如图所示，ABCD是边长为60 cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒.点E，F在边AB上，是被切去的一个等腰直角三角形斜边的两个端点.设AE＝FB＝x(cm).
某厂商要求包装盒的容积V(cm3)最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值.
令V′(x)＝0，得x＝0(舍去)或x＝20.∵当0