2020-2021学年广东省广州市番禺区桥城中学七年级（下）期中数学试卷（含解析）

这是一份2020-2021学年广东省广州市番禺区桥城中学七年级（下）期中数学试卷（含解析），共18页。试卷主要包含了5m2C，【答案】B，【答案】A，8080080008…等形式．，【答案】D，【答案】C等内容，欢迎下载使用。
 2020-2021学年广东省广州市番禺区桥城中学七年级（下）期中数学试卷副标题得分   下列图形中，与是内错角的是A.  B.  C.  D. 四个数，，，中，无理数的是A.  B.  C.  D. 如图，直线，，相交于一点，则的度数为
A.  B.  C.  D. 如图，轮船与灯塔相距，则下列说法中正确的是A. 轮船在灯塔的北偏西，处
B. 灯塔在轮船的北偏东，处
C. 轮船在灯塔的南偏东，处
D. 灯塔在轮船的南偏西，处
 如图，直线，将三角尺的直角顶点放在直线上，若，则等于
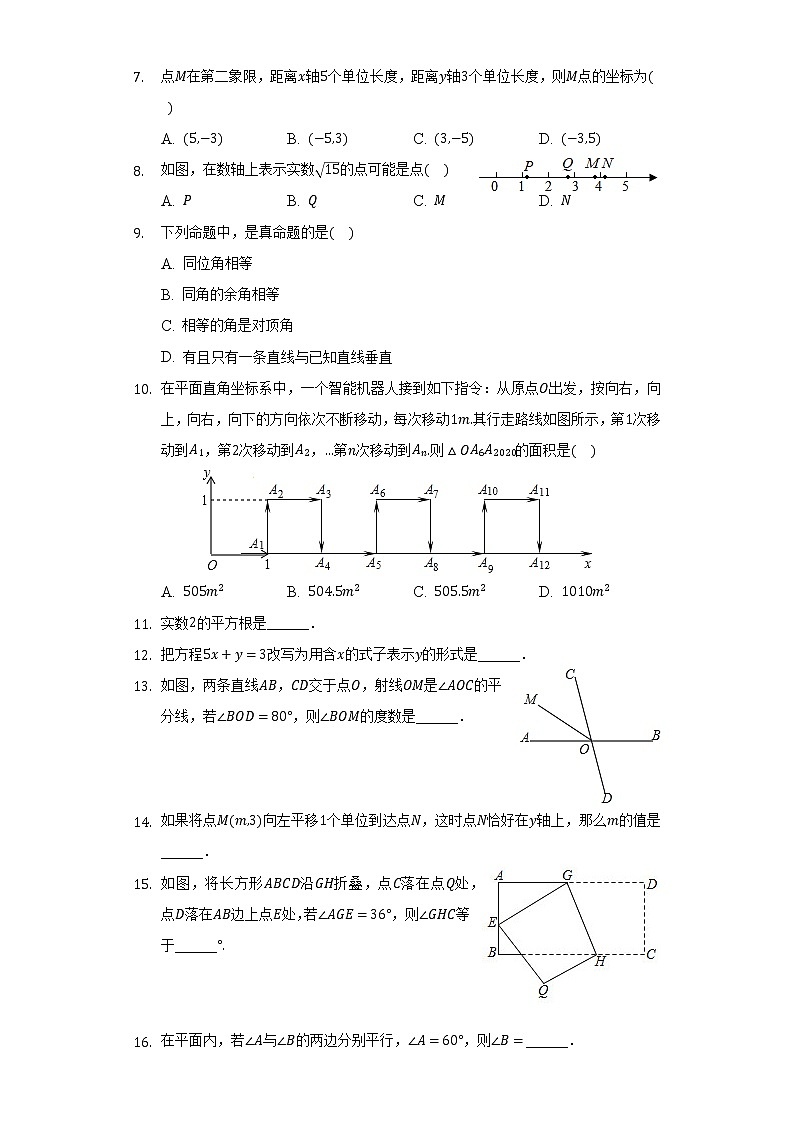
A.  B.  C.  D. 下列各组数中，是方程的解的是A.  B.  C.  D. 点在第二象限，距离轴个单位长度，距离轴个单位长度，则点的坐标为A.  B.  C.  D. 如图，在数轴上表示实数的点可能是点A.  B.  C.  D. 下列命题中，是真命题的是A. 同位角相等
B. 同角的余角相等
C. 相等的角是对顶角
D. 有且只有一条直线与已知直线垂直在平面直角坐标系中，一个智能机器人接到如下指令：从原点出发，按向右，向上，向右，向下的方向依次不断移动，每次移动其行走路线如图所示，第次移动到，第次移动到，第次移动到则的面积是
A.  B.  C.  D. 实数的平方根是______．把方程改写为用含的式子表示的形式是______．如图，两条直线，交于点，射线是的平分线，若，则的度数是______．

  如果将点向左平移个单位到达点，这时点恰好在轴上，那么的值是______．如图，将长方形沿折叠，点落在点处，点落在边上点处，若，则等于______

  在平面内，若与的两边分别平行，，则______．计算：．






 解方程组：






 在正方形网格中建立平面直角坐标系，使得，两点的坐标分别为，，过点作轴于点．
按照要求画出平面直角坐标系，线段，写出点的坐标；
求出以，，为顶点的三角形的面积．







 已知、满足，解关于的方程．






 如图，为直线上一点，为射线，，分别为，的平分线．
判断射线，的位置关系，并说明理由；
若，试说明为的平分线．






 列方程组解应用题
有大小两种货车，辆大货车与辆小货车一次可以运货吨，辆大货车与辆小货车一次可以运货吨，辆大货车与辆小货车一次可以运货多少吨？






 已知：如图，，．
判断与的位置关系，并说明理由．
若平分，平分，且，求的度数．







 当，都是实数，且满足，就称点为完美点．
判断点是否为完美点，并说明理由．
已知关于，的方程组，当为何值时，以方程组的解为坐标的点是完美点，请说明理由．






 如图，，直线与、分别交于点、，点在直线上，过点作，垂足为点．
求证：；
若点在线段上不与、、重合，连接，和的平分线交于点，请在图中补全图形，猜想并证明与的数量关系；
若直线的位置如图所示，中的结论是否成立？若成立，请证明；若不成立，请直接写出与的数量关系．








答案和解析 1.【答案】
 【解析】解：是同位角，故此选项错误；
B.是内错角，故此选项正确；
C.是同位角，故此选项错误；
D.不是内错角，故此选项错误；
故选B．
根据内错角的定义找出即可．
本题考查了同位角、内错角、同旁内角，熟记内错角的定义是解题的关键．
 2.【答案】
 【解析】解：，，是有理数，
是无理数，
故选：．
分别根据无理数、有理数的定义即可判定选择项．
此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如，，每两个之间依次多个等形式．
 3.【答案】
 【解析】解：如图，，

，
，
故选：．
根据对顶角的性质可，再根据平角的定义可求解．
本题主要考查对顶角，邻补角，掌握对顶角的性质是解题的关键．
 4.【答案】
 【解析】【分析】
本题考查了方向角的定义．用方向角描述方向时，通常以正北或正南方向为角的始边，以对象所处的射线为终边，故描述方向角时，一般先叙述北或南，再叙述偏东或偏西．注意几个方向的角平分线按日常习惯，即东北，东南，西北，西南，根据方向角的定义作出判断．
【解答】
解：灯塔在轮船的北偏东，处．
故选B．  5.【答案】
 【解析】解：如图，，
，
，
．
故选：．
根据平角的定义求出，再根据两直线平行，同位角相等可得．
本题考查了平行线的性质，熟记性质并准确识图是解题的关键．
 6.【答案】
 【解析】解：把，代入方程左边得：，右边，
左边右边，
则是方程的解．
故选：．
把各项中与的值代入方程检验即可．
此题考查了二元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值．
 7.【答案】
 【解析】解：点位于第二象限，
点的横坐标为负数，纵坐标为正数，
点距离轴个单位长度，距离轴个单位长度，
点的坐标为．
故选：．
首先确定点的横纵坐标的正负号，再根据距坐标轴的距离确定点的坐标．
此题主要考查了点的坐标，解决本题的关键是掌握好四个象限的点的坐标的特征：第一象限正正，第二象限负正，第三象限负负，第四象限正负．
 8.【答案】
 【解析】解：，
，
故选：．
估算出的范围即可得出答案．
本题考查了无理数的估算，无理数的估算常用夹逼法，用有理数夹逼无理数是解题的关键．
 9.【答案】
 【解析】解：、两直线平行，同位角相等，故此选项错误；
B、同角的余角相等，故此选项正确；
C、相等的角不一定是对顶角，故此选项错误；
D、过直线外一点，有且只有一条直线与已知直线垂直，故此选项错误．
故选：．
分析是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案．
此题主要考查了命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．
 10.【答案】
 【解析】解：由题意知，
，
，到轴距离为，
则的面积是
故选：．
由题意知，由，推出，到轴距离为，由此即可解决问题．
本题主要考查点的坐标的变化规律，解题的关键是根据图形得出下标为的倍数时对应长度即为下标的一半，据此可得．
 11.【答案】
 【解析】解：，
的平方根是．
故答案为：．
直接根据平方根的概念即可求解需注意一个正数有两个平方根．
本题主要考查了平方根的概念，比较简单．注意一个正数有两个平方根，它们互为相反数；的平方根是；负数没有平方根．
 12.【答案】
 【解析】解：，
．
故答案为：．
把看做已知数求出即可．
此题考查了解二元一次方程，解题的关键是将看做已知数求出．
 13.【答案】
 【解析】解：，
，，
射线是的平分线，
，
，
故答案为：．
先根据对顶角相等得出，再根据角平分线的定义得出，最后解答即可．
此题考查对顶角和角平分线的定义，关键是得出对顶角相等．
 14.【答案】
 【解析】解：将点向左平移个单位到达点，这时点恰好在轴上，
，
．
故答案为：．
根据向右平移横坐标加，向上平移纵坐标加即可得解．
本题考查了坐标与图形变化平移，熟记平移中点的变化规律：横坐标右移加，左移减；纵坐标上移加，下移减是解题的关键．
 15.【答案】
 【解析】解：，
，
由折叠可得，，
，
．
故答案为：．
由折叠可得，再根据平行线的性质即可得到．
本题主要考查了平行线的性质，解题时注意：两直线平行，同旁内角互补．
 16.【答案】或
 【解析】解：与的两边分别平行，
或，
，
，或．
故答案为：或．
由与的两边分别平行，可得或，继而求得答案．
此题考查了平行线的性质．注意由与的两边分别平行，可得与相等或互补是解题的关键．
 17.【答案】解：原式

．
 【解析】直接利用立方根的性质、二次根式的性质分别化简得出答案．
本题主要考查了立方根的性质、二次根式的性质、平方，正确化简各数是解题关键．
 18.【答案】解：
，得：，
解得：，
将代入，的：，
解得：，
则方程组的解为．
 【解析】利用加减消元法求解可得．
此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
 19.【答案】解：平面直角坐标系如图所示：

；
．
 【解析】根据、两点的坐标确定平面直角坐标系即可；
利用割补法，即可求出三角形的面积．
本题考查了坐标与图形的性质及三角形面积，掌握坐标的性质是解决问题的关键．
 20.【答案】解：，
，，
解得，，
，
．
 【解析】根据非负数的性质列出方程求出、的值，代入求方程的解即可．
本题考查了非负数的性质：几个非负数的和为时，这几个非负数都为．
 21.【答案】解：．
理由：，分别为，的平分线，
，，
，
，
．
，平分，

，
，
，
为的平分线．
 【解析】由角平分线的定义可求得，，结合平角的定义可求得，进而可说明与的关系；
由角平分线的定义可求解的度数，利用可求解的度数，进而可得，即可证明结论．
本题主要考查角平分线的定义，角的计算，灵活运用角平分线的定义求解角的关系是解题的关键．
 22.【答案】解：设一辆大货车一次可以运货吨，一辆小货车一次可以运货吨，
依题意，得：，
解得：，
．
答：辆大货车与辆小货车一次可以运货吨
 【解析】本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．
设一辆大货车一次可以运货吨，一辆小货车一次可以运货吨，根据“辆大货车与辆小货车一次可以运货吨，辆大货车与辆小货车一次可以运货吨”，即可得出关于，的二元一次方程组，解之即可得出，的值，再将其代入中即可得出结论．
 23.【答案】解：．
理由：，
，
又，
，
．

，
，
平分，
，
是的外角，
，
平分，
．
 【解析】根据平行线的性质即可得出，再根据条件，即可得到，进而判定．
根据平行线的性质，得到，根据三角形外角性质，即可得到，再根据角平分线的定义，即可得出的度数．
本题主要考查了平行线的性质与判定，角平分线的定义的综合应用，解题时注意：两直线平行，同位角相等；内错角相等，两直线平行．
 24.【答案】解：，可得，，可得，
，
不是完美点．

，
，
，可得，
，可得，
，
，
，
当时，点是完美点．
 【解析】根据完美点的定义判定即可；
用表示、，构建方程即可解决问题；
本题考查二元方程组，点的坐标等知识，解题的关键是理解题意，学会用转化的思想思考问题，属于创新题目．
 25.【答案】解：如图，，
，
是的外角，，
，
；

或，证明：
如图，当点在上时，

，
，
是的外角，
，
平分，平分，
，，
，
同理可得，，
，
又是的外角，
，
，即；
如图，当点在上时，

同理可得，，
又中，，
，即；

中的结论不成立．存在：；．
如图，当点在上时，由，可得：

，
，
，
又是的外角，
，
，
即；
如图，当在上时，

同理可得，，
，
，
又中，，
，
．
 【解析】依据平行线的性质以及三角形外角性质，即可得到；
分两种情况讨论：当点在上时，依据平行线的性质以及三角形外角性质，；当点在上时，依据平行线的性质以及三角形外角性质，；
分两种情况讨论：当点在上时，依据平行线的性质以及三角形外角性质，；当在上时，依据平行线的性质以及三角形外角性质，．
本题考查了平行线的性质，角平分线的定义的运用，准确识图并理清图中各角度之间的关系是解题的关键，难点在于利用三角形外角性质进行计算．