2020-2021学年黑龙江省哈尔滨市第十七中学八年级（下）期中教学质量检测数学试卷

哈十七中学八年级（下）期中教学质量检测数学试卷

一、选择题（每题3分，共计30分）

1. 下列方程中，一定是关于的一元二次方程的是（    ）

A.  B.

C.  D.

2. 如图所示的图象分别给出了x与y的对应关系，其中表示y是x的函数的是（　　）

A.  B.

C.  D.

3. 已知在中，，，，那么的长为（    ）

A. 2 B.  C. 3 D.

4. 下列满足条件的三角形中，不是直角三角形的是（    ）

A. 三内角之比为1∶2∶3 B. 三边长的平方之比为1∶2∶3

C. 三边长之比为3∶4∶5 D. 三内角之比为3∶4∶5

5. 下列四个命题中不正确是（    ）

A. 对角线相等的菱形是正方形 B. 有两边相等的平行四边形是菱形

C. 对角线相等的平行四边形是矩形 D. 对角线互相平分的四边形是平行四边形

6. 用配方法解方程3x2－4x－2＝0时，配方正确的是(    )

A. (x＋)2＝ B. (x－)2＝

C. (x＋)2＝ D. (x－)2＝

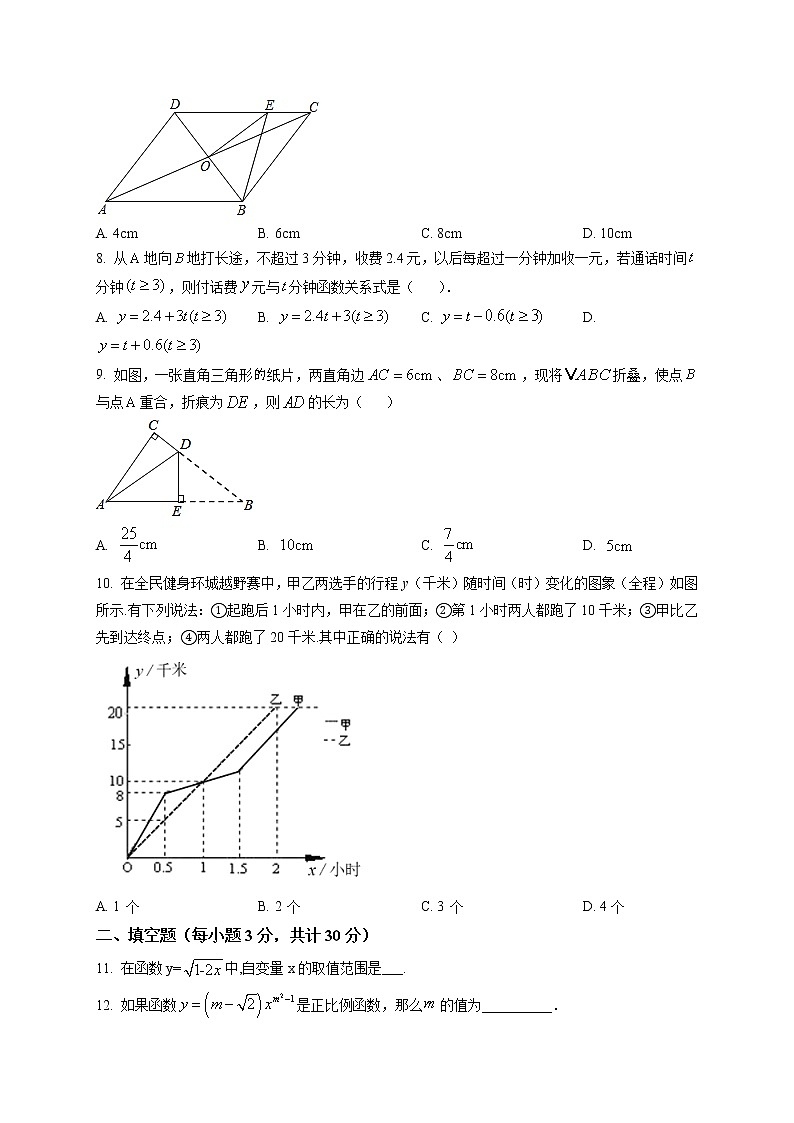
7. 如图，平行四边形周长为，对角线与相交于点，交于，连接，则的周长为（    ）

A. 4cm B. 6cm C. 8cm D. 10cm

8. 从地向地打长途，不超过3分钟，收费2.4元，以后每超过一分钟加收一元，若通话时间分钟，则付话费元与分钟函数关系式是（    ）．

A.  B.  C.  D.

9. 如图，一张直角三角形纸片，两直角边、，现将折叠，使点与点重合，折痕为，则的长为（    ）

A.  B.  C.  D.

10. 在全民健身环城越野赛中，甲乙两选手的行程y（千米）随时间（时）变化的图象（全程）如图所示.有下列说法：①起跑后1小时内，甲在乙的前面；②第1小时两人都跑了10千米；③甲比乙先到达终点；④两人都跑了20千米.其中正确的说法有（ ）

A. 1 个 B. 2 个 C. 3 个 D. 4个

二、填空题（每小题3分，共计30分）

11. 在函数y=中,自变量x的取值范围是___.

12. 如果函数是正比例函数，那么的值为__________．

13. 若是一元二次方程的一个根，则_______．

14. 正比例函数，随增大而减小，则的取值范围是_______．

15. 已知关于x的一元二次方程（m﹣1）x2+x+1=0有实数根,则m的取值范围是______________．

16. 如图，正方形，延长至，使，则的度数_______．

17. 有一间长20m，宽15m的会议室，在它的中间铺一块地毯，地毯的面积是会议室面积的，四周未铺地毯的留空宽度相同，则留空宽度为_____m．

18. 在平行四边形中，，、的平分线分别交于点、，，则平行四边形的周长为_______．

19. 如图，在直线上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是、、、，则_______．

20. 如图，四边形是菱形，，点是上一点，，点是延长线上一点，且，则菱形的周长是_______．

三、解答题（21、22题各7分，23、24题各8分，25-27题各10分，共计60分）

21. 解下列方程：（1）        （2）

22. 如图，在每个小正方形的边长为的方格纸中有线段和，点、、、均在小正方形的顶点上．

（1）在方格纸中画出菱形，点、均在小正方形的顶点上，且菱形的面积为；

（2）在方格纸中画出为斜边的等腰直角，点在正方形的顶点上；

（3）在（1）（2）条件下，连接，请直接写出的长．

23. 如图，一艘轮船位于灯塔B的正西方向A处，且A处与灯塔B相距60海里，轮船沿东北方向匀速航行，到达位于灯塔B的北偏东l5°方向上的C处．

(1)求∠ACB的度数；

(2)求灯塔B到C处的距离．(结果保留根号)

24. 如图1，在中，，平分，是的中点，连接，过点作，交的延长线于点，连接．

（1）求证：四边形是矩形；

（2）如图2，若是上一动点（点不与、重合），连接、、，在不添加任何辅助线的情况下，直接写出图2中与四边形面积相等的所有三角形和四边形（四边形除外）．

25. 随着人们环保意识的不断增强，我市家庭电动自行车的拥有量逐年增加，据统计，某小区2016年底拥有家庭电动自行车125辆，2018年底家庭电动自行车的拥有量达到180辆．

（1)若该小区2016年底到2018年底家庭电动自行车拥有量的平均增长率相同，按照这个增长速度该小区2019年底家庭电动自行车将达到多少辆？

（2）为了缓解停车矛盾，该小区决定再建40个停车位，据测算，建造费用分别为室内车位1000元/个，露天车位200元/个，考虑到实际因素，该小区计划投资费用不超过20000元，则该小区最多可建室内车位多少个？

26. 如图1，在中，，点、分别在、上，连接，点是延长线上一点，连接，．

（1）求证：；

（2）如图2，过点作交于点，延长与交于点，过点作交延长线于点，连接，，求证：；

（3）如图3，在（2）问条件下，延长分别交、延长线于点、，点是上一点，连接，当，，四边形面积为9时，求的长．

27. 如图1，在平面直角坐标系中，，点在第一象限且横坐标为，连接、，面积为6．

（1）求直线的解析式；

（2）如图2，点在上且横坐标为，连接，的面积用表示，求与的函数关系式（不需要写自变量取值范围）；

（3）如图3，在（2）问条件下，点在延长线上，连接、，点为OP上一点，连接并延长交于点，过点作于点，连接，当，，时，求的长．

参考答案

1-5. DDDDB       6-10. BCCAC

11. x≤     12.     13.      14.

15. m≤且m≠1       16.       17.

18. 32或40       19. 4               20. 84

21. 解：（1）∵，

∴，，，

∴，

∴，

∴，；

（2）∵，

∴，

∴，

∴，．

22. （1）如图所示：

∵AB=EF=5，AF=BE=

∴四边形ABEF菱形

（2）如图所示：

∵

∴是等腰直角三角形．

（3）．

23. （1）在△ABC中，∠CAB=45°，∠CBA=90°+15°=105°．则∠ACB=180°-45°-105°=30°，即∠ACB=30°；
 

（2）过点B作AC的垂线，垂足为D，依题意可得∠DAB=45°，∠DBA=45°，AB=60海里．

AD=BD=AB⋅sin45∘=60×.
在△BDC中，∠DBC=45°+15°=60°，∠BDC=90°，cos∠DBC==cos60°=．
∴BC=60（海里）．
答：灯塔B到C处的距离是60海里．

24. 解：（1）∵CE∥AD，∴∠DAO=∠ECO，∠ADO=∠CEO，

∵O是AC的中点，∴AO=CO，

∴△OCE≌△OAD（AAS），∴AD=CE，∴四边形ADCE是平行四边形，

∵AB=AC，AD平分∠ABC，∴AD⊥BC，∴∠ADC=90°，∴四边形ADCE是矩形；

（2）∵四边形ADCE是矩形，

∴AD∥CE，AE∥CD，

∴（同底等高），（同底等高）

∵四边形ABDF的面积，

∴四边形ABDF的面积，

∵AB=AC，AD平分∠ABC，

∴BD=CD，

∴,

∴四边形ABDF的面积，

综上所述，四边形ABDF的面积．

25. 解：（1）设该小区2016年底到2018年底家庭电动自行车拥有量的平均增长率为x，

依题意，得：125（1+x）2=180，

解得：x1=0.2=20%，x2=-2.2（舍去），

∴180×（1+x）=180×（1+20%）=216．

答：按照这个增长速度该小区2019年底家庭电动自行车将达到216辆．

（2）设该小区可建室内车位m个，则可建露天车位（40-m）个，

依题意，得：1000m+200（40-m）≤20000，

解得：m≤15．

答：该小区最多可建室内车位15个．

26. 解：（1）∵∠C=90°，

∴∠B+∠BAC=90°，

∵∠DAB=∠B−∠AEF，

∴∠DAB+∠AEF+∠BAC=90°，即∠DAE+∠AED=90°，

∴∠AED=180°-∠DAE-∠AED=90°，

∴AD⊥DE；

（2）∵∠C=90°，FN∥BC，

∴∠FNC=∠ANF=90°，∠NCM=90°

∴∠CNQ=90°，

∵QM⊥BM，

∴∠QMC=90°，

∴四边形CMQN是矩形，

∴CM=NQ，

∵AF=AQ，∠ANF=90°，

∴FN=NQ=CM，

∴

∴△FNE≌△MCE（AAS），

∴NE=CE；

（3）如图所示，过点R作RH⊥AK于H，

由（2）得△FNE≌△MCE，

∴NE=CE，FE=EM，CM=FN=NQ

∵PQ∥KM，

∴△DPF∽△DKM，

∴，

∵FM=6DF，

∴，

∴，

∵∠ACK=∠EDA=∠KHR=90°，

∴∠K+∠KAC=90°，∠AED+∠KAC=90°，

∴∠K=∠EAD，

又∵AE=KR=PR，

∴△HRK≌△DAE（AAS），KH=HP，

∴DE=AH=HP=EF+DF=4DF，

∴PK=PH+KH=8DF，

∴，

∴，

∴

设DF=x

∵∠PDF=∠ENF=90°，∠PFD=∠EFN，

∴△PFD∽EFN，

∴，

∴，，

∴

∵RH⊥AK，MD⊥AK，

∴HR∥MD，

∴△KHR∽△KDM，

∴，

∴，

∴，

∴，

∴，

∵，

∴，

解得，

∴．

27. （1）设解析式为，B纵坐标为y

的面积等于OA×y÷2=6

故有，解得，

将代入，得k=1

∴OB所在直线的解析式为

（2）P点横坐标为t，根据P处在直线，所以P点纵坐标为t

△POA的面积为OA×t÷2=

△OAB的面积为OA×÷2=÷2=6

△ABP的面积为：S=△OAB的面积-△POA的面积=12-=

故有S=

（3）∵B点在OB直线上

∴

∵P为平行四边形对角线中点

∴P点横纵坐标都是B点横纵坐标的

∴

设M（m,n）

∵PM=1

∴

∴ ①式

∵BM⊥AE

∴BM²+AM²=AB²

∴ ②式

联立①②得:；

设直线AM解析式为

∴ 解得

∴直线AM的解析式为：

∵四边形OABC为平行四边形

∴BC=OA

∴

设OC直线解析式为

代入点C坐标求得

∴OC直线解析式为

联立 得   

∴

∴ ∵四边形ABCO为平行四边形 ∴CO=AB=

∴