

中考复习之二次函数压轴之面积问题-含详细参考答案学案
展开二次函数压轴之面积问题
问题简介:
1.抛物线y=x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,直线y=kx-3,经过点B,C.
(1)求抛物线的解析式
(2)点P是直线BC下方抛物线上一动点,求PBC面积最大时点P的坐标;
2.如图,在平面直角坐标系中,已知抛物线y=x2﹣2x﹣3与x轴交于点A和点B,点A在点B的左侧,与y轴交于点C.
(1)求A点、C点的坐标;
(2)点P是第四象限内的抛物线上一点,连接AC,CP,BP,若四边形ACPB面积为请求出此时点P的坐标;
3.如图,抛物线y=与x轴交于A,B两点(点A在点B的左侧),顶点为D.点P为对称轴右侧抛物线上的一个动点,其横坐标为m,直线AD交y轴于点C,过点P作PF∥AD,交x轴于点F,PE∥x轴,交直线AD于点E,交直线DF于点M.
(1)求直线AD的表达式及点C的坐标;
(2)当四边形AFPE的面积与△ADF的面积相等时,求m的值;
4.如图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)设点Q是抛物线上的一个动点,是否存在一点Q,使S△QAB=S△CAB,若存在,直接写出Q点的坐标;若不存在,请说明理由.
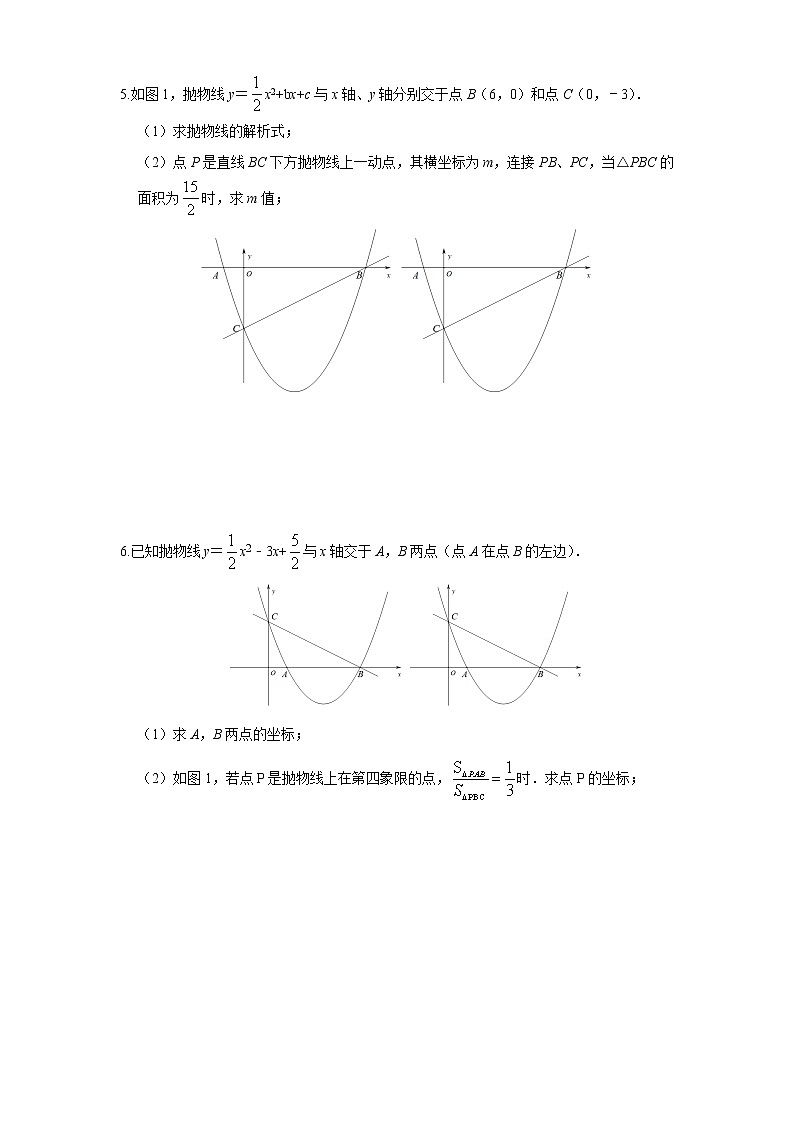
5.如图1,抛物线y=x2+bx+c与x轴、y轴分别交于点B(6,0)和点C(0,﹣3).
(1)求抛物线的解析式;
(2)点P是直线BC下方抛物线上一动点,其横坐标为m,连接PB、PC,当△PBC的面积为时,求m值;
6.已知抛物线y=x2﹣3x+与x轴交于A,B两点(点A在点B的左边).
(1)求A,B两点的坐标;
(2)如图1,若点P是抛物线上在第四象限的点,时.求点P的坐标;
7.已知二次函数y=ax2+bx+2(a≠0)交x轴于点A,B(点A在点B左侧),AB=3,交y轴于点C,设抛物线的对称轴为直线x=m,且m≥0.
(1)用含m的代数式表示出点A、点B的坐标;
(2)若抛物线上存在点P使得S△ABP=S△ABC=3(点P与点C不重合),且这样的点P恰好存在两个,求此时抛物线的解析式;
8.如图,在平面直角坐标系中,一抛物线的对称轴为直线x=﹣1,与y轴负半轴交于点C,与x轴交于A,B两点,其中点A的坐标为(﹣3,0),且OA=OC,D为抛物线的顶点.
(1)求抛物线的解析式;
(2)若M(﹣2,y)是抛物线上一点,P是抛物线上另一点(点P与点D不重合),当S△BDM=S△BPM时,求出此时点P的坐标;
9.如图,抛物线y=﹣x2+bx+c过点A(﹣1,0)和点B(3,0),与y轴交于点C在x轴上有一动点E(m,0)(其中m为实数,0<m<3),过动点E作直线l⊥x轴,交抛物线于点M.
(1)求抛物线解析式及点C的坐标;
(3)连接BM并延长交y轴于点N,连接AM,OM若△AEM的面积等于△MON面积的2倍,求m的值.
10.如图1,抛物线y=ax2﹣2ax+b(a<0)与x轴交于A、B两点(A点在B点的左边),与y轴的正半轴交于点C,顶点为D,OB=OC=3OA.
(1)求抛物线解析式;
(2)如图2,点E的坐标为(0,7),若过点E作一条直线与抛物线在对称轴右侧有且只有一个交点H,直线y=kx﹣2k﹣5(k≠0)与抛物线交于F、G两点,求当k为何值时,△FGH面积最小,并求出面积的最小值;
参考答案
- 解:方法一:过点P作PD||y轴交BC于点D,设P(m,m2-2m-3),易知BC的解析式为y=x-3,则D(m,m-3)铅垂高PD=m-3-(m2-2m-3)=-m2+3m水平宽xB-xC=3,S△PBC=(-m2+3m),当m=时,△PBC的面积取最大值,此时P(,)
方法二:将BC向下平移,当它与抛物线相切时,此时△PBC的面积最大设平移后的直线l解析式为y=x+m与抛物线y=x2-2x-3联立得x2-3x-(m+3)=0,此时△=0,即有9+4(m+3)=0,m=此时方程的根为x1=x2=,P点的坐标为(,)
方法三:过点P作EF||x轴,过点B作BF⊥EF于点F,设P(m,m2-2m-3)S△PBC=
S四EFBO-S△BOC-S△PCE-S△PBF=(-(m2-2m-3)-(3-m)(m2-2m-3)-m(-(m2-2m-3-3)=(-m2+3m),当m=时,△PBC的面积取最大值,此时P(,)
- 解:(1)A(-1,0),C(0,-3)
(2)易知AB=4,OC=3,故S△ABC=6,而S四ACBP=S△ABC+S△BCP,故S△BCP=设P(m,m2-2m-3),直线BC的解析式为y=x-3,过点P作PD||y轴交BC于点D,则D(m,m-3),PD=m-3-(m2-2m-3)=-m2+3m,S△BCP=(-m2+3m)=得m1=,m2=,此时P点的坐标为(,)或(,)
- 解:(1)y=x+,C(0,)
(2) 作DG、PH垂直于x轴于点G、H,P(m,),PH=||
SAFPE=AF∙PH,S△ADF=AF∙DG,即有||=2,解得m1=1+,m2=1-(舍去)m3=1+,m4=1-(舍去),故m的值为1+或1+
- 解:(1)y=-x2+2x+3
(2)作CD||y交AB于点D,易知直线AB的解析式为y=-x+3,故D(1,2),SABC=3,
方法一:设Q(m,-m2+2m+3)则E(m,-m+3),则QE=|-m2+2m+3-(-m+3)|=|-m2+3m|
SABQ=|-m2+3m|=3,解得m1=1,m2=2,m3=,m4=,故Q点的坐标为(1,4)或(2,3)或(,)或(,)
- 解:(1)y=x2-x-3
(3) 易知直线BC的解析式为y=x-3设P(m,m2-m-3),E(m,m-3),PE=m-3-(m2-m-3)=-m2+3m,SPBC=∙6∙(-m2+3m)=,解得m1=1,m2=5
- 解:(1)A(1,0),B(5,0)y=x2﹣3x+
(2)易知直线BC的解析式为y=-x+,设P(m,m2﹣3m+),则E(m,-m+),PE=-m+-(m2﹣3m+)=-m2+m,SPBC=(-m2+m),而SPAB=2(m2﹣3m+),得
- 解:(1)A(m-1.5,0)B(m+1.5,0)
(2)1.a<0时,x轴下方恰好存在两个纵坐标为-2的点,而x轴上方有且仅有一点C,则C为最高点时,满足题意,故b=0,对称轴为直线x=0,m=0,得a=-,抛物线的解析式为y=-x2+2
- a>0时,x轴上方有一个纵坐标为2的点,x轴下方有一个纵坐标为-2的点,故(m,-2)为其顶点,设y=a(x-m)2-2,点B(m+1.5,0)和(0,2)代入得a=,m=,故抛物线的解析式为y=(x-)2-2
- 解:(1)y=x2+2x-3
(2) 易知M(-2,-3)故直线BM的解析式为y=x-,D(-1,-4)过点D、P分别作DE、PF平行于y轴,E(-1,-),故DE=,S△BDM=∙3=,设P(m,m2+2m-3)则F(m,m-)
PF=|m--(m2+2m-3)|=|-m2+m+|,故S△BMP=∙3|-m2+m+|=,解得m1=0,m2=-3(舍),m3=,m4=,故点P的坐标为(0,-3)或(,)或(,)
- 解:(1)y=-x2+2x+3
(3) E(m,0),M(m,-m2+2m+3),直线BM的表达式为y=(-m-1)x+3m+3,x=0时,y=3m+3,
故N(0,3m+3),SAEM=,2SMON=(3m+3)m,即=(3m+3)m,解得m=-2或-1(舍去负值),故m=-2
- 解:(1)y=-x2+2x+3
(2) 设直线EH的解析式为y=mx+7,与抛物线y=-x2+2x+3联立得x2+(m-2)x+4=0,=0,即有(m-2)2=16,得m=-2或6(舍),y=-2x+7,H(2,3)而M(2,-5),HM=8;联立y=kx-2k-5抛物线y=-x2+2x+3得x2+(k-2)x-2k-8=0,xF+xG=2-k,xF∙xG=-2k-8, xG-xF=,
SFGH=4,当k=-2时,面积最小,最小值为16
数学八年级上册19.6 轨迹导学案及答案: 这是一份数学八年级上册19.6 轨迹导学案及答案,共7页。
2022中考数学压轴题复习之二次函数压轴之线段最值问题-含详细参考答案学案: 这是一份2022中考数学压轴题复习之二次函数压轴之线段最值问题-含详细参考答案学案,共13页。
中考复习之二次函数与几何综合学案-附练习题含参考答案: 这是一份中考复习之二次函数与几何综合学案-附练习题含参考答案,共7页。学案主要包含了知识与方法归纳,练习题等内容,欢迎下载使用。












