







2020-2021学年8.5 空间直线、平面的平行说课课件ppt
展开基本事实1过不在一条直线上的三个点,有且只有一个平面.基本事实1给出了确定一个平面的依据.它也可以简单说成“不共线的三点确定一个平面. 基本事实2如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内. 利用基本事实2,可以判断直线是否在平面内.
基本事实3如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线. 基本事实3告诉我们,如果两个平面有一个公共点,那么这两个平面一定相交于过这个公共点的一条直线.指出了两个平面相交成一条直线的事实. 上述三个关于平面的 基本事实是人们经过长期观察与实践总结出来的,是几何推理的基本依据,也是我们进一步研究立体图形的基础、
利用基本事实1和基本事实2,再结合“ 两点确定一条直线”, 可以得到下面三个推论. 推论1经过一条直线和这条直线外一点,有且只有一个平面.推论2经过两条相交直线,有且只有一个平面. 推论3经过两条平行直线,有且只有一个平面.
空间点、直线、平面之间的位置关系
1.空间中直线与直线的位置关系共面直线:相交直线:在同一平面内,有且只有一个公共点.平行直线:在同一平面内,没有公共点 异面直线:不同在任何一个平面内,没有公共点. 2.空间中直线与平面的位置关系 (1)直线在平面内一 有无数个公共点; (2) 直线与平面相交一 有且只有一个公共点;(3) 直线与平面平行一 没有公共点 3.空间中平面与平面的位置关系 (1)两个平面平行一 没有公共点;(2) 两个平面相交一 有一条公共直线.
在平面几何的学习中,我们研究过两条直线的位置关系,重点研究了两条直线平行,得到了这种特殊位置关系的性质,以及判定两条直线平行的定理.类似地,空间中直线、平面间的平行关系在生产和生活中有着广泛的应用,也是我们要重点研究的内容.
我们知道,在同一平面内,不相交的两条直线是平行直线,并且当两条直线都与第三条直线平行时,这两条直线互相平行.在空间中,是否也有类似的结论?
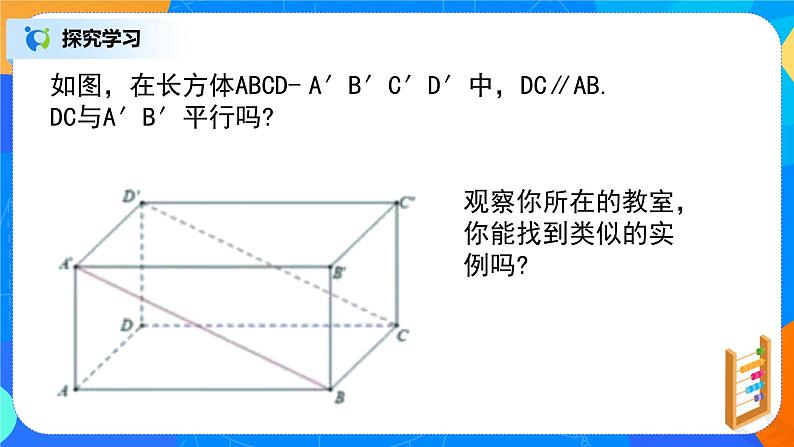
如图,在长方体ABCD- A′B′C′D′中,DC∥AB. DC与A′B′平行吗?
观察你所在的教室,你能找到类似的实例吗?
观察我们所在的教室黑板边所在直线AA′和门框所在直线CC′都平行于墙与墙的交线BB′,那么CC′∥AA′ 这说明空间中的平行直线具有与平面内的平行直线类似的性质.
基本事实4平行于同一直线的两条直线平行.
文字语言平行于同一条直 线的两条直线平行图形语言:
符号语言:直线a, b, Cc若a//b, b//c,则a∥c 作用:证明或判断两条直线平行 说明:基本事实4表述的性质通常叫做平行的传递性
观察:将一张纸如图进行折叠,则各折痕及边a, b, C, d, e...之间有何关系?
a//b //c //d //e //... 推广:在空间平行于一条已知直线的所有直线都互相平行.
它给出了判断空间两条直线平行的依据.
例1如图, 空间四边形ABCD中,E,F,G,H分别是边AB, BC, CD, DA的中点.求证:四边形EFGH是平行四边形.
分析:要证明四边形EFGH是平行四边形,只需证明它的一组对边平行且相等.而EH,FG分别是MABD和△CBD的中位线,从而它们都与BD平行且等于BD的一半.应用基本事实4,即可证明EH与FG平行且相等.
证明:连接BD.因为EH是AABD的 中位线, 所以EH//BD,且EH=(1/2)BD. 同理FG//BD, 且FG=(1/2)BD. 所以EH与FG平行 且相等. 所以四边形EFGH为平行四边形.
例2如图, 在正方体ABCD- ABCD中,M, M分别是棱AD和AD、的中点。
(1) 求证:四边形BBM.M为平行四边形; (2) 求证:∠BM,C =∠BMC.
分析: (1) 通过基本事实4证明MM,// BB,且MM = BB;(2) 由(1) 知B.M,// BM, 同理证得CM,//CM, 再由等角定理证得∠BMC=∠B、M,C.也可以通过证明ABCM与△BCM全等证出∠BMC=∠B,M,C.
证明: (1)在正方形ADD4中,M,M.分别为AD, AD的中点,所以MM,// AA.又AA// BB,所以MM // BB且MM, = BB,所以四边形BB.M,M为平行四边形. (2)方法一:由(1)知四边形BB.M.M为平行四边形,所以B.M//BM.由(1)同理可得四边形CCMM为平行四边形,所以CM, //CM.由平面几何知识可知,∠BMC和∠B.MC都是锐角,所以∠BMC=∠B.MC. 方法二:由(1) 知四边形BBM.M为平行四边形,所以B.M[// BM.由(1)同理可得四边形CCMM为平行四边形,所以CM = CM.又B,C= BC,所以△BCM与ABCM全等,所以∠BMC= CB,MC.
说明:证明角相等,利用空间等角定理是常用的思考方法;另外也可以 通过证明两个三角形全等或相似来证明两角相等.在应用等角定理时,应注意当两个角的两边分别对应平行且方向都相同或相反时,这两个角相等,否则这两个角互补.因此,在证明两个角相等时,只说明两个角的两边分别对应平行是不够的.
基本事实4:平行于同一直线的两条直线平行. 符号语言:直线a, b, c若a//b, b//c,则a∥c 作用:证明或判断两条直线平行 说明:基本事实4表述的性质通常叫做平行的传递性
人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行公开课ppt课件: 这是一份人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行公开课ppt课件,文件包含人教A版2019高一必修2数学851直线与直线平行课件pptx、人教A版2019高一必修2数学851直线与直线平行教案doc等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
人教A版 (2019)必修 第二册8.5 空间直线、平面的平行评课ppt课件: 这是一份人教A版 (2019)必修 第二册8.5 空间直线、平面的平行评课ppt课件,共24页。PPT课件主要包含了点与直线,点与平面,直线与直线,直线与平面,平面与平面,基本事实4,符号语言,公理作用,图形语言,等角定理等内容,欢迎下载使用。
人教A版 (2019)必修 第二册8.5 空间直线、平面的平行精品ppt课件: 这是一份人教A版 (2019)必修 第二册8.5 空间直线、平面的平行精品ppt课件














