高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.6 空间直线、平面的垂直课堂教学ppt课件

这是一份高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.6 空间直线、平面的垂直课堂教学ppt课件，文件包含8632平面与平面垂直pptx、8632平面与平面垂直docx等2份课件配套教学资源，其中PPT共15页， 欢迎下载使用。
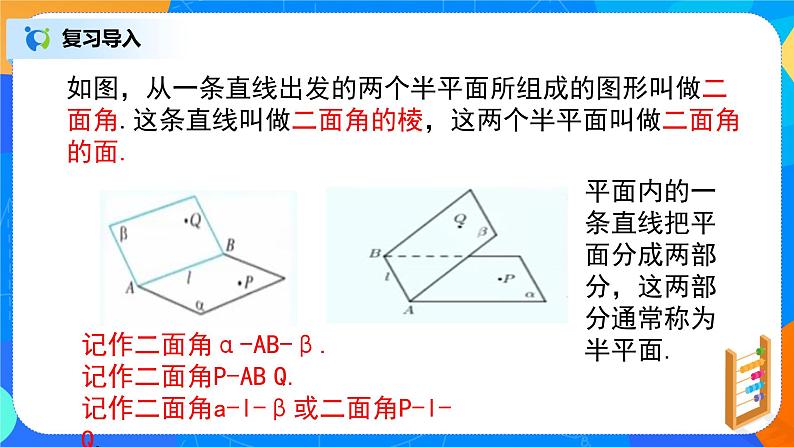
如图，从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱，这两个半平面叫做二面角的面.
记作二面角α-AB-β. 记作二面角P-AB Q. 记作二面角a-l-β或二面角P-l-Q.
平面内的一条直线把平面分成两部分，这两部分通常称为半平面.
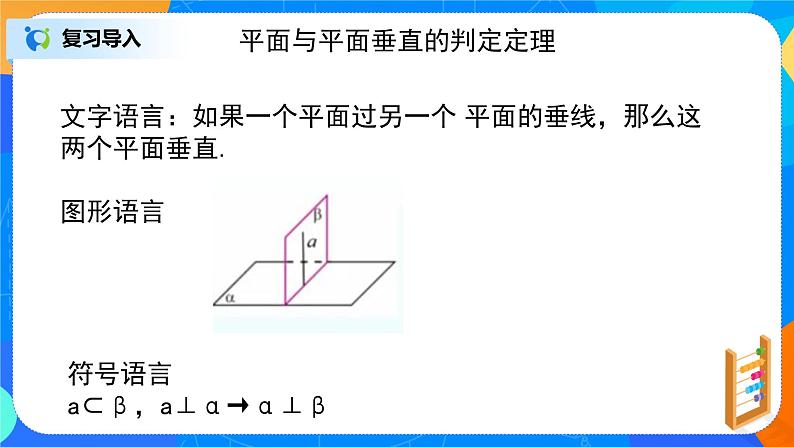
文字语言：如果一个平面过另一个 平面的垂线，那么这两个平面垂直. 图形语言
符号语言 a⊂β，a⊥α→α⊥β
平面与平面垂直的判定定理
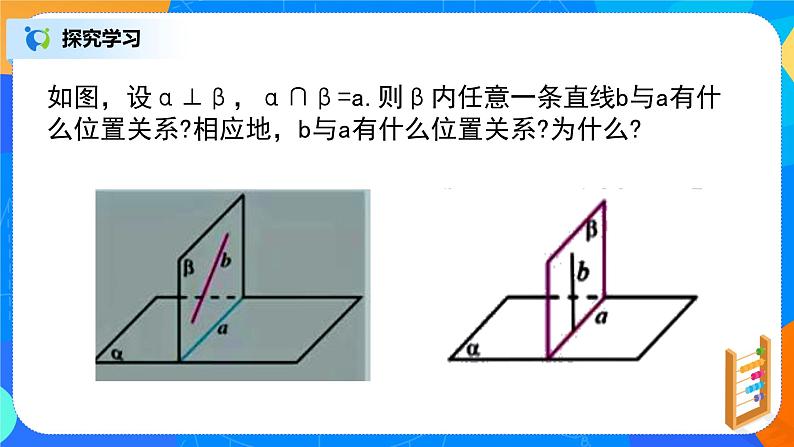
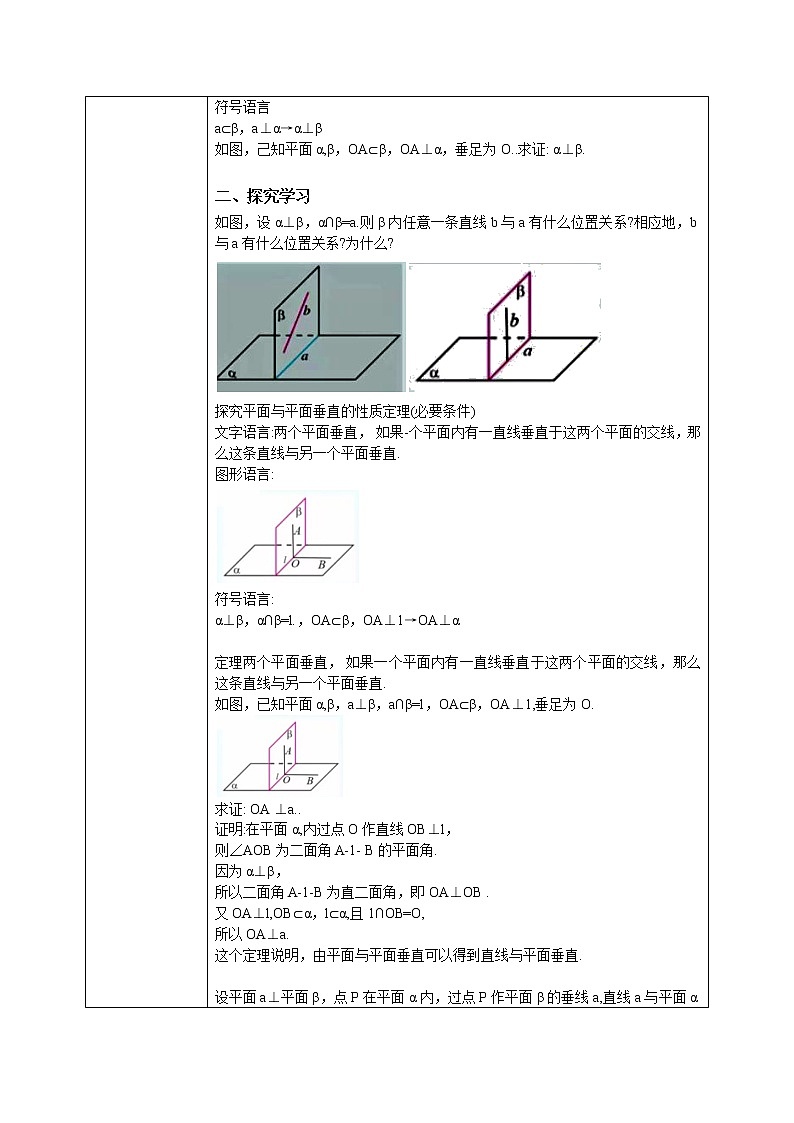
如图，设α⊥β，α∩β=a.则β内任意一条直线b与a有什么位置关系?相应地，b与a有什么位置关系?为什么?
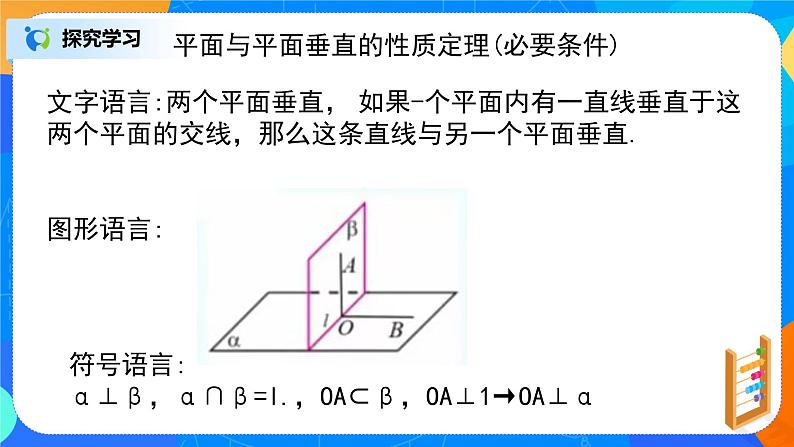
平面与平面垂直的性质定理(必要条件)
文字语言:两个平面垂直， 如果-个平面内有一直线垂直于这两个平面的交线，那么这条直线与另一个平面垂直. 图形语言:
符号语言: α⊥β，α∩β=l.，OA⊂β，OA⊥1→OA⊥α
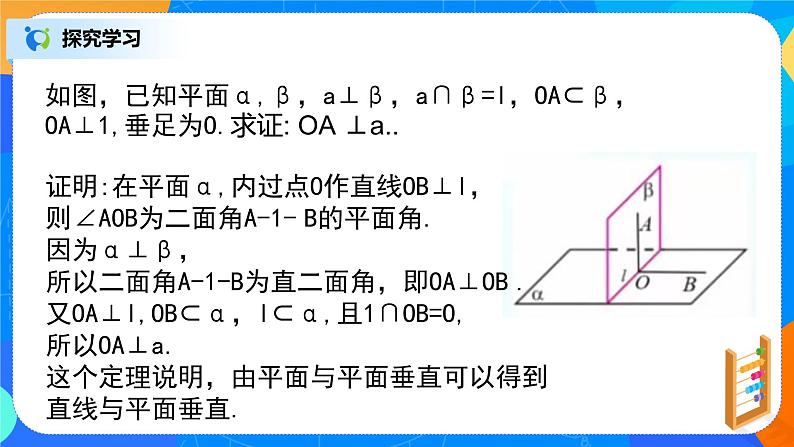
如图，已知平面α,β，a⊥β，a∩β=l，OA⊂β，OA⊥1,垂足为O.求证: OA ⊥a..
证明:在平面α,内过点O作直线OB⊥l， 则∠AOB为二面角A-1- B的平面角. 因为α⊥β， 所以二面角A-1-B为直二面角，即OA⊥OB . 又OA⊥l,OB⊂α，l⊂α,且1∩OB=O, 所以OA⊥a. 这个定理说明，由平面与平面垂直可以得到直线与平面垂直.
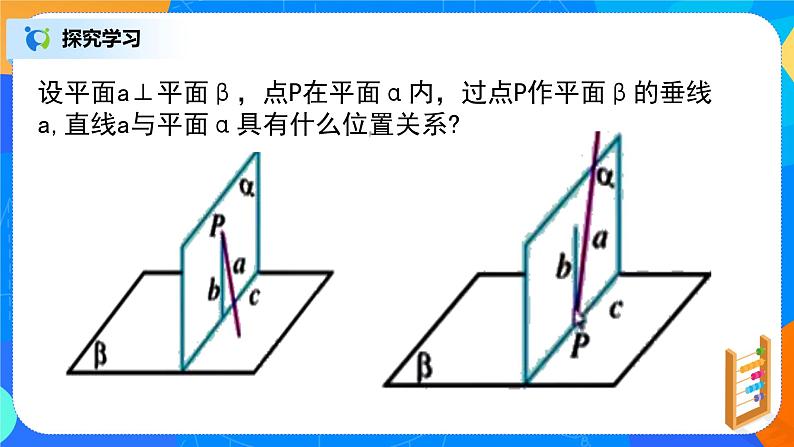
设平面a⊥平面β，点P在平面α内，过点P作平面β的垂线a,直线a与平面α具有什么位置关系?
如图，设a∩β=c，过点P在平面α内作直线b⊥c，根据平面与平面垂直的性质定理，b⊥β.因为过一点有且只有一条直线与平面β垂直，所以直线a与直线b重合，因此a⊂α.
例1如图， 已知平面α⊥平面β，直线a⊥β，a⊄α,判断a与α的位置关系.
解:设a∩β=1，在a内作直线b,满足b⊥1, 由α⊥β, 则b⊥β. 又a⊥β， 则a//b . 又a⊄α则 a//a.
例2如图， 已知PA⊥平面ABC，平面PAB⊥平面PBC，求证: BC⊥平面PAB.
证明:过点A作AE⊥PB，垂足为E. 由平面PAB⊥平面PBC，平面PAB∩平面PBC= PB, 则AE⊥平面PBC. 由BC⊂平面PBC, 则AE⊥BC. 由 PA⊥平面ABC，BC⊂平面ABC, 则 PA⊥BC. 又PA∩AE=A， 则 BC⊥平面PAB.