预测12 【精品】二次函数-2022年中考数学三轮冲刺过关（全国通用）

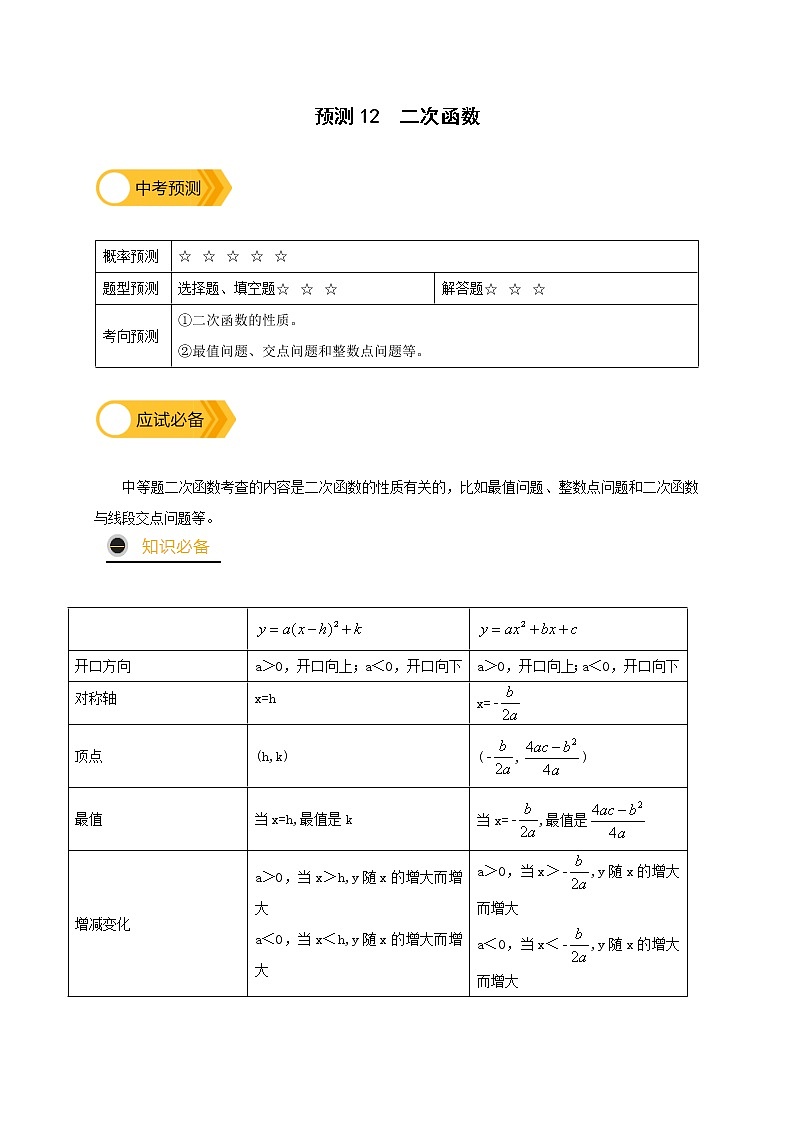
预测12  二次函数

中等题二次函数考查的内容是二次函数的性质有关的，比如最值问题、整数点问题和二次函数与线段交点问题等。

二次函数最值问题需要考虑是自变量在对称轴的同侧或异侧，分情况讨论，利用二次函数的性质去确定最值。二次函数与线段有交点问题，有时需要讨论二次函数与一次函数联立组成方程的△，因为自变量有范围，不仅需要讨论△，还要再做进一步的分析。

1.（2021·安徽中考真题）已知抛物线的对称轴为直线．

（1）求a的值；（2）若点M（x1，y1），N（x2，y2）都在此抛物线上，且，．比较y1与y2的大小，并说明理由；（3）设直线与抛物线交于点A、B，与抛物线交于点C，D，求线段AB与线段CD的长度之比．

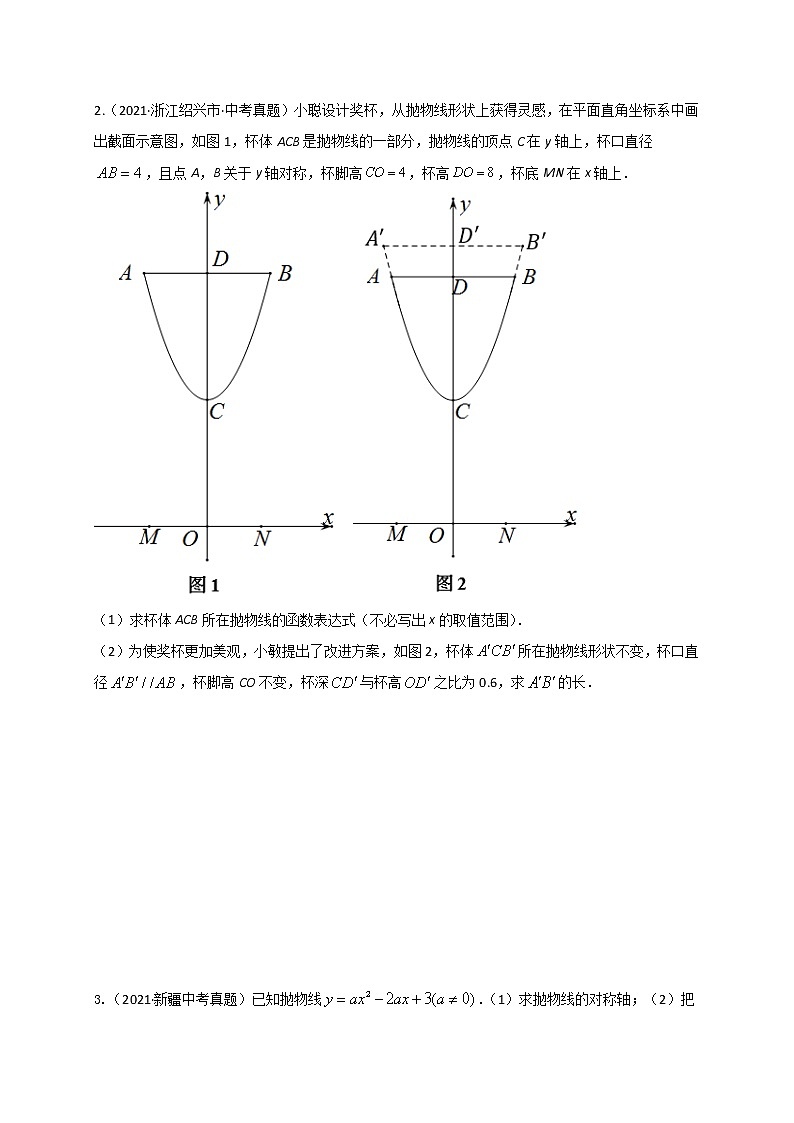
2.（2021·浙江绍兴市·中考真题）小聪设计奖杯，从抛物线形状上获得灵感，在平面直角坐标系中画出截面示意图，如图1，杯体ACB是抛物线的一部分，抛物线的顶点C在y轴上，杯口直径，且点A，B关于y轴对称，杯脚高，杯高，杯底MN在x轴上．

（1）求杯体ACB所在抛物线的函数表达式（不必写出x的取值范围）．

（2）为使奖杯更加美观，小敏提出了改进方案，如图2，杯体所在抛物线形状不变，杯口直径，杯脚高CO不变，杯深与杯高之比为0.6，求的长．

3.（2021·新疆中考真题）已知抛物线．（1）求抛物线的对称轴；（2）把抛物线沿y轴向下平移个单位，若抛物线的顶点落在x轴上，求a的值；（3）设点，在抛物线上，若，求a的取值范围．

4.（2021·湖南长沙市·中考真题）我们不妨约定：在平面直角坐标系中，若某函数图象上至少存在不同的两点关于轴对称，则把该函数称之为“T函数”，其图象上关于轴对称的不同两点叫做一对“T点”．根据该约定，完成下列各题．（1）若点与点是关于的“T函数”的图象上的一对“T点”，则______，______，______（将正确答案填在相应的横线上）；

（2）关于的函数（，是常数）是“T函数”吗？如果是，指出它有多少对“T点”；如果不是，请说明理由；（3）若关于的“T函数”（，且，，是常数）经过坐标原点，且与直线（，，且，是常数）交于，两点，当，满足时，直线是否总经过某一定点？若经过某一定点，求出该定点的坐标；否则，请说明理由．

5.（2021·陕西中考真题）已知抛物线与x轴交于点A、B（其中A在点B的左侧），与y轴交于点C．（1）求点B、C的坐标；（2）设点与点C关于该抛物线的对称轴对称在y轴上是否存在点P，使与相似且与是对应边？若存在，求点P的坐标；若不存在，请说明理由．

6.（2021·浙江杭州市·中考真题）在直角坐标系中，设函数（，是常数，）．

（1）若该函数的图象经过和两点，求函数的表达式，并写出函数图象的顶点坐标．

（2）写出一组，的值，使函数的图象与轴有两个不同的交点，并说明理由．

（3）已知，当（，是实数，）时，该函数对应的函数值分别为，．若，求证．

7.（2021·四川乐山市·中考真题）已知关于的一元二次方程．

（1）若方程有两个不相等的实数根，求的取值范围；

（2）二次函数的部分图象如图所示，求一元二次方程的解．

8.（2021·浙江温州市·中考真题）已知抛物线经过点．

（1）求抛物线的函数表达式和顶点坐标．

（2）直线交抛物线于点，，为正数．若点在抛物线上且在直线下方（不与点，重合），分别求出点横坐标与纵坐标的取值范围，

9.（2021·浙江嘉兴市·中考真题）已知二次函数．

（1）求二次函数图象的顶点坐标；（2）当时，函数的最大值和最小值分别为多少？

（3）当时，函数的最大值为，最小值为，m-n=3求的值．

10.（2021·浙江中考真题）如图，已知经过原点的抛物线与轴交于另一点A(2，0)．

（1）求的值和抛物线顶点的坐标；（2）求直线的解析式．

11.（2021·广东中考真题）已知抛物线

（1）当时，请判断点（2，4）是否在该抛物线上；

（2）该抛物线的顶点随着m的变化而移动，当顶点移动到最高处时，求该抛物线的顶点坐标；

（3）已知点、，若该抛物线与线段EF只有一个交点，求该抛物线顶点横坐标的取值范围．

12.（2021·山东中考真题）在平面直角坐标系中，抛物线的顶点为A．

（1）求顶点A的坐标（用含有字母m的代数式表示）；

（2）若点，在抛物线上，且，则m的取值范围是          ；（直接写出结果即可）

（3）当时，函数y的最小值等于6，求m的值．

13.（2021年河南中考真题）如图，抛物线与直线交于点A(2，0)和点．

（1）求和的值；

（2）求点的坐标，并结合图象写出不等式的解集；

（3）点是直线上的一个动点，将点向左平移个单位长度得到点，若线段与抛物线只有一个公共点，直接写出点的横坐标的取值范围．

1．（广东省广州市越秀区八一实验中学2020-2021学年九年级下学期中考数学二模试卷）已知抛物线，（，为常数）．

（1）若抛物线的顶点坐标为，求，的值；

（2）若抛物线上始终存在不重合的两点关于原点对称，求的取值范围；

（3）在（1）的条件下，存在正实数，，当时，恰好有，求，的值．

2．（2021年河南省南阳市淅川县九年级第一次模拟测试数学试题）在平面直角坐标系中，函数y＝x2－2ax－1（a为常数）的图象与y轴交于点A．

（1）求点A的坐标．

（2）当此函数图象经过点（1，2）时，求此函数的表达式，并写出函数值y随x的增大而增大时x的取值范围．

（3）当x≤0时，若函数y＝x2－2ax－1（a为常数）的图象的最低点到直线y＝2a的距离为2，求a的值．

3． （2021年福建省厦门市松柏中学九年级中考二模数学试题）已知，抛物线y＝ax2，其中a＞0

（1）若抛物线经过点A（－1，2），求此抛物线的解析式

（2）如图1，若点A、B是此抛物线上两点，且分属于y轴两侧，连接AB与y轴相交于点C，且∠AOB＝90°．求证：CO＝；

（3）如图2，若点A是此抛物线上一点，过点A的直线恰好与此抛物线仅有一个交点，且与y轴交于点B，与x轴相交于点C．求证：AC＝BC．

4.(吉林省第二实验学校2020-2021学年九年级下学期第二次模拟数学试题)已知，点是平面直角坐标系内的一点，将点绕坐标原点逆时针旋转得到点，经过、、三点的二次函数的图象记为．

（1）若点的坐标为．

①点的坐标为___________．

②求图象所对应的函数表达式．

（2）若点的坐标为，图象所对应的函数表达式为（、为常数，）．写出的值，并用含的代数式表示．（直接写出即可）

（3）在（2）条件下，直线与图象交于点，直线与图象交于点．图象在、之间的部分（包含、两点）记为．

①当图象在上的函数值随自变量的增大而增大时，设图象的最高点的纵坐标为，最低点的纵坐标为，记，求的取值范围．

②连结，当与图象围成的封闭图形与轴交于点（点不与坐标原点重合）．当时，直接写出的取值范围．

5.（2021年河南省三甲名校中考数学内部押题试卷（一））把抛物线先向右平移4个单位长度，再向下平移5个单位长度得到抛物线．

（1）直接写出抛物线的函数关系式；

（2）动点能否在拋物线上？请说明理由；

（3）若点都在抛物线上，且，比较的大小，并说明理由．

6.（2021年福建省泉州市惠安县中考数学质检试卷）已知抛物线与轴交于和两点，与轴交于点，且．对于该抛物线上的任意两点，，，，当时，总有．

（1）求抛物线的解析式；

（2）若过点的直线与该抛物线交于另一点，与线段交于点．作，与交于点，求的最大值，并求此时点的坐标；

（3）若直线与抛物线交于，两点，不与，重合），直线，分别与轴交于点，，设，两点的纵坐标分别为，，试探究、之间的数量关系．

7.（2021年河南省新乡市辉县市中考模拟数学试题）如图，在平面直角坐标系中，已知二次函数图象的顶点为A，与y轴交于点B，异于顶点A的点C(1，n)在该函数图象上．

（1）当m=5时，求n的值．

（2）当n=2时，若点A在第一象限内，结合图象，求当y时，自变量x的取值范围．

（3）作直线AC与y轴相交于点D.当点B在x轴上方，且在线段OD上时，求m的取值范围．