备战中考初中数学导练学案50讲—第04讲一元一次方程及其应用（讲练版）

这是一份备战中考初中数学导练学案50讲—第04讲一元一次方程及其应用（讲练版），共18页。学案主要包含了疑难点拨，基础训练，能力提升，探索发现等内容，欢迎下载使用。
备战中考初中数学导练学案50讲
第04讲 一元一次方程及其应用
【疑难点拨】
1.解一元一次方程的易错点：易错点1　移项不变号导致错误；易错点2　去括号漏乘导致错误；易错点3　去分母漏乘导致错误；易错点4　分母小数化整数多乘导致错误
2.一元一次方程应用题解题：（1）方法一、直列法。即由题中的“和”、“少”、“倍”等表示数量关系的字眼，直接列出相关的方程。（2）公式法。学生熟识的公式诸如“路程＝速度×时间”、“工作总量＝工作效率×工作时间”、“利润＝售价－进价”、“利润率＝利润/进价”等都是解答相关方程应用题的工具。（3）总分法。即根据总量等于各分量之和来列出方程，用此法要注意分量不可有所遗漏。（4）同一法。这类题目的解题原理是：如果同一个量能用两个不同的代数式表达，则这两个代数式必然相等。
【基础篇】
一、选择题：
1. 下列方程中，是一元一次方程的是（　　）
A．x2﹣4x=3 B．x=0 C．x+2y=1 D．x﹣1=
2. 方程2x+a﹣4=0的解是x=﹣2，则a等于（　　）
A．﹣8 B．0 C．2 D．8
3. （2018•临安区）中央电视台2套“开心辞典”栏目中，有一期的题目如图所示，两个天平都平衡，则三个球体的重量等于（　　）个正方体的重量．

A．2 B．3 C．4 D．5
4. （2018•四川成都•3分）已知 ，且 ，则的值为（ ）．
A．12 B．13 C．14 D．15
5. （2018•南通模拟）篮球比赛规定：胜一场得3分，负一场得1分，某篮球队共进行了6场比赛，得了12分，该队获胜的场数是（　　）
A．2 B．3 C．4 D．5
二、填空题：
6. 如果关x的方程与的解相同，那么m的值是 　．
7. （2018•曲靖）一个书包的标价为115元，按8折出售仍可获利15%，该书包的进价为　 　元．
8. （2018·湖北江汉·3分）某公司积极开展“爱心扶贫”的公益活动，现准备将6000件生活物资发往A，B两个贫困地区，其中发往A区的物资比B区的物资的1.5倍少1000件，则发往A区的生活物资为　 件．
三、解答与计算题：
9. （2018·四川省攀枝花）解方程：﹣=1．




10. （2018•张家界）列方程解应用题
《九章算术》中有“盈不足术”的问题，原文如下：“今有共買羊，人出五，不足四十五；人出七，不足三．问人数、羊價各幾何？”题意是：若干人共同出资买羊，每人出5元，则差45元；每人出7元，则差3元．求人数和羊价各是多少？





【能力篇】
一、选择题：
11. （2018•湖北恩施•3分）一商店在某一时间以每件120元的价格卖出两件衣服，其中一件盈利20%，另一件亏损20%，在这次买卖中，这家商店（　　）
A．不盈不亏 B．盈利20元 C．亏损10元 D．亏损30元
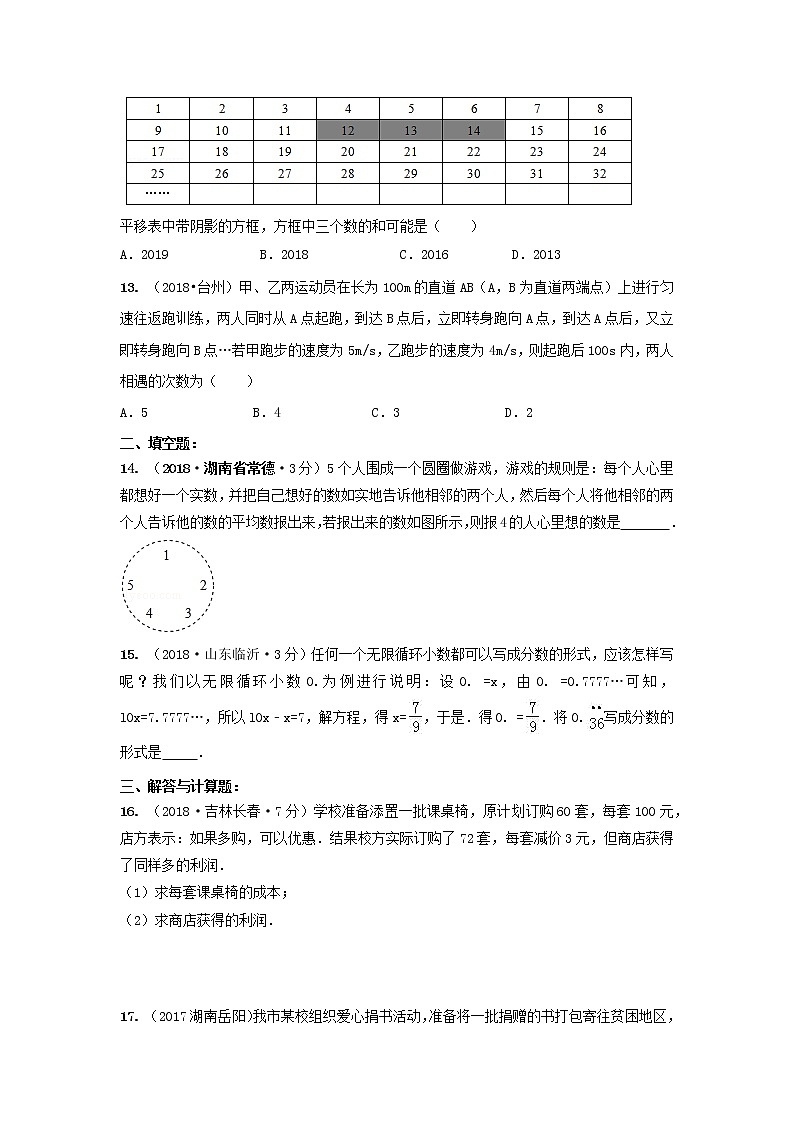
12. （2018·湖北省武汉·3分）将正整数1至2018按一定规律排列如下表：

平移表中带阴影的方框，方框中三个数的和可能是（　　）
A．2019 B．2018 C．2016 D．2013
13. （2018•台州）甲、乙两运动员在长为100m的直道AB（A，B为直道两端点）上进行匀速往返跑训练，两人同时从A点起跑，到达B点后，立即转身跑向A点，到达A点后，又立即转身跑向B点…若甲跑步的速度为5m/s，乙跑步的速度为4m/s，则起跑后100s内，两人相遇的次数为（　　）
A．5 B．4 C．3 D．2
二、填空题：
14. （2018·湖南省常德·3分）5个人围成一个圆圈做游戏，游戏的规则是：每个人心里都想好一个实数，并把自己想好的数如实地告诉他相邻的两个人，然后每个人将他相邻的两个人告诉他的数的平均数报出来，若报出来的数如图所示，则报4的人心里想的数是　 　．

15. （2018·山东临沂·3分）任何一个无限循环小数都可以写成分数的形式，应该怎样写呢？我们以无限循环小数0.为例进行说明：设0. =x，由0. =0.7777…可知，l0x=7.7777…，所以l0x﹣x=7，解方程，得x=，于是．得0. =．将0.写成分数的形式是　 　．
三、解答与计算题：
16. （2018·吉林长春·7分）学校准备添置一批课桌椅，原计划订购60套，每套100元，店方表示：如果多购，可以优惠．结果校方实际订购了72套，每套减价3元，但商店获得了同样多的利润．
（1）求每套课桌椅的成本；
（2）求商店获得的利润．


17. （2017湖南岳阳）我市某校组织爱心捐书活动，准备将一批捐赠的书打包寄往贫困地区，其中每包书的数目相等．第一次他们领来这批书的，结果打了16个包还多40本；第二次他们把剩下的书全部取来，连同第一次打包剩下的书一起，刚好又打了9个包，那么这批书共有多少本？




18. 公园门票价格规定如下表：
购票张数
1～50张
51～100张
100张以上
每张票的价格
13元
11元
9元
某校初一（1）、（2）两个班共104人去游公园，其中（1）班人数较少，不足50人．
经估算，如果两个班都以班为单位购票，则一共应付1240元，问：
（1）两班各有多少学生？
（2）如果两班联合起来，作为一个团体购票，可省多少钱？
（3）如果初一（1）班单独组织去游公园，作为组织者的你将如何购票才最省钱？






【探究篇】
19. （2018•随州）我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式（整数可看作分母为1的分数），那么无限循环小数如何表示为分数形式呢？请看以下示例：
例：将0.化为分数形式
由于0. =0.777…，设x=0.777…①
则10x=7.777…②
②﹣①得9x=7，解得x=，于是得0. =．
同理可得0. = =，1. =1+0. =1+=
根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）
【基础训练】
（1）0. =　　，5. =　　；
（2）将0. 化为分数形式，写出推导过程；
【能力提升】
（3）0. 1=　 　，2.0=　 　；
（注：0. 1=0.315315…，2.0=2.01818…）
【探索发现】
（4）①试比较0.与1的大小：0.　 　1（填“＞”、“＜”或“=”）
②若已知0. 8571=，则3. 1428=　 　．
（注：0. 857l=0.285714285714…）


20. 已知数轴上点A与16个单位长度，点A在原点的左侧，到原点的距离为26个单位长度，点B在点A的右侧，点C表示的数与点B表示的数互为相反数，动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．
（1）点A表示的数为___________，点B表示的数为___________，点C表示的数为___________．
（2）用含t的代数式表示P到点A和点C的距离： PA= ，PC=___________．

（3）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动， Q点到达C点后，再立即以同样的速度返回，运动到终点A．
①在点Q向点C运动过程中，能否追上点P?若能，请求出点Q运动几秒追上．


②在点Q开始运动后，P、Q两点之间的距离能否为2个单位？如果能，请求出此时点P表示的数；如果不能，请说明理由．




























第04讲 一元一次方程及其应用
【疑难点拨】
1.解一元一次方程的易错点：易错点1　移项不变号导致错误；易错点2　去括号漏乘导致错误；易错点3　去分母漏乘导致错误；易错点4　分母小数化整数多乘导致错误
2.一元一次方程应用题解题：（1）方法一、直列法。即由题中的“和”、“少”、“倍”等表示数量关系的字眼，直接列出相关的方程。（2）公式法。学生熟识的公式诸如“路程＝速度×时间”、“工作总量＝工作效率×工作时间”、“利润＝售价－进价”、“利润率＝利润/进价”等都是解答相关方程应用题的工具。（3）总分法。即根据总量等于各分量之和来列出方程，用此法要注意分量不可有所遗漏。（4）同一法。这类题目的解题原理是：如果同一个量能用两个不同的代数式表达，则这两个代数式必然相等。
【基础篇】
一、选择题：
1. 下列方程中，是一元一次方程的是（　　）
A．x2﹣4x=3 B．x=0 C．x+2y=1 D．x﹣1=
【考点】一元一次方程的定义．
【分析】只含有一个未知数（元），并且未知数的指数是1（次）的方程叫做一元一次方程．它的一般形式是ax+b=0（a，b是常数且a≠0）．
【解答】解：A、x2﹣4x=3的未知数的最高次数是2次，不是一元一次方程，故A错误；
B、x=0符合一元一次方程的定义，故B正确；
C、x+2y=1是二元一次方程，故C错误；
D、x﹣1=，分母中含有未知数，是分式方程，故D错误．
故选：B．
【点评】本题主要考查了一元一次方程的一般形式，只含有一个未知数，未知数的最高次数是1，一次项系数不是0，这是这类题目考查的重点．
2. 方程2x+a﹣4=0的解是x=﹣2，则a等于（　　）
A．﹣8 B．0 C．2 D．8
【考点】方程的解．
【分析】方程的解就是能够使方程左右两边相等的未知数的值，即利用方程的解代替未知数，所得到的式子左右两边相等．
【解答】解：把x=﹣2代入方程2x+a﹣4=0，
得到：﹣4+a﹣4=0
解得a=8．
故选D．
【点评】本题主要考查了方程解的定义，已知x=﹣2是方程的解实际就是得到了一个关于a的方程．
3. （2018•临安区）中央电视台2套“开心辞典”栏目中，有一期的题目如图所示，两个天平都平衡，则三个球体的重量等于（　　）个正方体的重量．

A．2 B．3 C．4 D．5
【分析】由图可知：2球体的重量=5圆柱体的重量，2正方体的重量=3圆柱体的重量．可设一个球体重x，圆柱重y，正方体重z．根据等量关系列方程即可得出答案．
【解答】解：设一个球体重x，圆柱重y，正方体重z．
根据等量关系列方程2x=5y；2z=3y，消去y可得：x=z，
则3x=5z，即三个球体的重量等于五个正方体的重量．
故选：D．
4. （2018•四川成都•3分）已知 ，且 ，则的值为（ ）．
A．12 B．13 C．14 D．15
【答案】12
【考点】解一元一次方程，比例的性质
【解析】【解答】解：设 则a=6k，b=5k，c=4k
∵
∴6k+5k-8k=6，解之：k=2
∴a=6×2=12
故答案为：12，故选A。
【分析】设 ，分别用含k的式子表示出a、b、c的值，再根据 ，建立关于k的方程，求出k的值，就可得出a的值。
5. （2018•南通模拟）篮球比赛规定：胜一场得3分，负一场得1分，某篮球队共进行了6场比赛，得了12分，该队获胜的场数是（　　）
A．2 B．3 C．4 D．5
【分析】设该队获胜x场，则负了（6﹣x）场，根据总分=3×获胜场数+1×负了的场数，即可得出关于x的一元一次方程，解之即可得出结论．
【解答】解：设该队获胜x场，则负了（6﹣x）场，
根据题意得：3x+（6﹣x）=12，
解得：x=3．
答：该队获胜3场．
故选：B．
二、填空题：
6. 如果关x的方程与的解相同，那么m的值是 　．
【考点】同解方程．
【分析】本题中有两个方程，且是同解方程，一般思路是：先求出不含字母系数的方程的解，再把解代入到含有字母系数的方程中，求字母系数的值．
【解答】解：解方程=
整理得：15x﹣3=42，
解得：x=3，
把x=3代入=x+4+2|m|
得=3++2|m|
解得：|m|=2，
则m=±2．
故答案为±2．
【点评】本题考查了同解方程，使方程左右两边相等的未知数的值是该方程的解，因此检验一个数是否为相应的方程的解，就是把这个数代替方程中的未知数，看左右两边的值是否相等．
7. （2018•曲靖）一个书包的标价为115元，按8折出售仍可获利15%，该书包的进价为　 　元．
【分析】设该书包的进价为x元，根据销售收入﹣成本=利润，即可得出关于x的一元一次方程，解之即可得出结论．
【解答】解：设该书包的进价为x元，
根据题意得：115×0.8﹣x=15%x，
解得：x=80．
答：该书包的进价为80元．
故答案为：80．
8. （2018·湖北江汉·3分）某公司积极开展“爱心扶贫”的公益活动，现准备将6000件生活物资发往A，B两个贫困地区，其中发往A区的物资比B区的物资的1.5倍少1000件，则发往A区的生活物资为　 件．
【分析】设发往B区的生活物资为x件，则发往A区的生活物资为（1.5x﹣1000）件，根据发往A.B两区的物资共6000件，即可得出关于x的一元一次方程，解之即可得出结论．
【解答】解：设发往B区的生活物资为x件，则发往A区的生活物资为（1.5x﹣1000）件，
根据题意得：x+1.5x﹣1000=6000，
解得：x=2800，
∴1.5x﹣1000=3200．
答：发往A区的生活物资为3200件．
故答案为：3200．
三、解答与计算题：
9. （2018·四川省攀枝花）解方程：﹣=1．
解：去分母得：3（x﹣3）﹣2（2x+1）=6，
去括号得：3x﹣9﹣4x﹣2=6，
移项得：﹣x=17，
系数化为1
得：x=﹣17．
10. （2018•张家界）列方程解应用题
《九章算术》中有“盈不足术”的问题，原文如下：“今有共買羊，人出五，不足四十五；人出七，不足三．问人数、羊價各幾何？”题意是：若干人共同出资买羊，每人出5元，则差45元；每人出7元，则差3元．求人数和羊价各是多少？
【分析】可设买羊人数为未知数，等量关系为：5×买羊人数+45=7×买羊人数+3，把相关数值代入可求得买羊人数，代入方程的等号左边可得羊价．
【解答】解：设买羊为x人，则羊价为（5x+45）元钱，
5x+45=7x+3，
x=21（人），
5×21+45=150（员），
答：买羊人数为21人，羊价为150元．
【能力篇】
一、选择题：
11. （2018•湖北恩施•3分）一商店在某一时间以每件120元的价格卖出两件衣服，其中一件盈利20%，另一件亏损20%，在这次买卖中，这家商店（　　）
A．不盈不亏 B．盈利20元 C．亏损10元 D．亏损30元
【分析】设两件衣服的进价分别为x、y元，根据利润=销售收入﹣进价，即可分别得出关于x、y的一元一次方程，解之即可得出x、y的值，再用240﹣两件衣服的进价后即可找出结论．
【解答】解：设两件衣服的进价分别为x、y元，
根据题意得：120﹣x=20%x，y﹣120=20%y，
解得：x=100，y=150，
∴120+120﹣100﹣150=﹣10（元）．
故选：C．
【点评】本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．
12. （2018·湖北省武汉·3分）将正整数1至2018按一定规律排列如下表：

平移表中带阴影的方框，方框中三个数的和可能是（　　）
A．2019 B．2018 C．2016 D．2013
【分析】设中间数为x，则另外两个数分别为x﹣1、x+1，进而可得出三个数之和为3x，令其分别等于四个选项中数，解之即可得出x的值，由x为整数、x不能为第一列及第八列数，即可确定x值，此题得解．
【解答】解：设中间数为x，则另外两个数分别为x﹣1、x+1，
∴三个数之和为（x﹣1）+x+（x+1）=3x．
根据题意得：3x=2019、3x=2018、3x=2016、3x=2013，
解得：x=673，x=672（舍去），x=672，x=671．
∵673=84×8+1，
∴2019不合题意，舍去；
∵672=84×8，
∴2016不合题意，舍去；
∵671=83×7+7，
∴三个数之和为2013．
故选：D．
【点评】本题考查了一元一次方程的应用以及规律型中数字的变化类，找准等量关系，正确列出一元一次方程是解题的关键．
13. （2018•台州）甲、乙两运动员在长为100m的直道AB（A，B为直道两端点）上进行匀速往返跑训练，两人同时从A点起跑，到达B点后，立即转身跑向A点，到达A点后，又立即转身跑向B点…若甲跑步的速度为5m/s，乙跑步的速度为4m/s，则起跑后100s内，两人相遇的次数为（　　）
A．5 B．4 C．3 D．2
【分析】可设两人相遇的次数为x，根据每次相遇的时间，总共时间为100s，列出方程求解即可．
【解答】解：设两人相遇的次数为x，依题意有
x=100，
解得x=4.5，
∵x为整数，
∴x取4．
故选：B．
二、填空题：
14. （2018·湖南省常德·3分）5个人围成一个圆圈做游戏，游戏的规则是：每个人心里都想好一个实数，并把自己想好的数如实地告诉他相邻的两个人，然后每个人将他相邻的两个人告诉他的数的平均数报出来，若报出来的数如图所示，则报4的人心里想的数是　 　．

【分析】设报4的人心想的数是x，则可以分别表示报1，3，5，2的人心想的数，最后通过平均数列出方程，解方程即可．
【解答】解：设报4的人心想的数是x，报1的人心想的数是10﹣x，报3的人心想的数是x﹣6，报5的人心想的数是14﹣x，报2的人心想的数是x﹣12，
所以有x﹣12+x=2×3，
解得x=9．
故答案为9．
【点评】本题属于阅读理解和探索规律题，考查的知识点有平均数的相关计算及方程思想的运用．规律与趋势：这道题的解决方法有点奥数题的思维，题意理解起来比较容易，但从哪下手却不容易想到，一般地，当数字比较多时，方程是首选的方法，而且，多设几个未知数，把题中的等量关系全部展示出来，再结合题意进行整合，问题即可解决．本题还可以根据报2的人心想的数可以是6﹣x，从而列出方程x﹣12=6﹣x求解．
15. （2018·山东临沂·3分）任何一个无限循环小数都可以写成分数的形式，应该怎样写呢？我们以无限循环小数0.为例进行说明：设0. =x，由0. =0.7777…可知，l0x=7.7777…，所以l0x﹣x=7，解方程，得x=，于是．得0. =．将0.写成分数的形式是　 　．
【分析】设0. =x，则36. =100x，二者做差后可得出关于x的一元一次方程，解之即可得出结论．
【解答】解：设0. =x，则36. =100x，
∴100x﹣x=36，
解得：x=．
故答案为：．
【点评】本题考查了一元一次方程的应用，找准等量关系，正确列出一元一次方程是解题的关键．
三、解答与计算题：
16. （2018·吉林长春·7分）学校准备添置一批课桌椅，原计划订购60套，每套100元，店方表示：如果多购，可以优惠．结果校方实际订购了72套，每套减价3元，但商店获得了同样多的利润．
（1）求每套课桌椅的成本；
（2）求商店获得的利润．
【分析】（1）设每套课桌椅的成本为x元，根据利润=销售收入﹣成本结合商店获得的利润不变，即可得出关于x的一元一次方程，解之即可得出结论；
（2）根据总利润=单套利润×销售数量，即可求出结论．
【解答】解：（1）设每套课桌椅的成本为x元，
根据题意得：60×100﹣60x=72×（100﹣3）﹣72x，
解得：x=82．
答：每套课桌椅的成本为82元．
（2）60×（100﹣82）=1080（元）．
答：商店获得的利润为1080元．
【点评】本题考查了一元一次方程的应用，解题的关键是：（1）找准等量关系，正确列出一元一次方程；（2）根据数量关系，列式计算．
17. （2017湖南岳阳）我市某校组织爱心捐书活动，准备将一批捐赠的书打包寄往贫困地区，其中每包书的数目相等．第一次他们领来这批书的，结果打了16个包还多40本；第二次他们把剩下的书全部取来，连同第一次打包剩下的书一起，刚好又打了9个包，那么这批书共有多少本？
【分析】设这批书共有3x本，根据每包书的数目相等．即可得出关于x的一元一次方程，解之即可得出结论．
【解答】解：设这批书共有3x本，
根据题意得： =，
解得：x=500，
∴3x=1500．
答：这批书共有500本．
【点评】本题考查了一元一次方程的应用，根据每包书的数目相等．列出关于x的一元一次方程是解题的关键．
18. 公园门票价格规定如下表：
购票张数
1～50张
51～100张
100张以上
每张票的价格
13元
11元
9元
某校初一（1）、（2）两个班共104人去游公园，其中（1）班人数较少，不足50人．
经估算，如果两个班都以班为单位购票，则一共应付1240元，问：
（1）两班各有多少学生？
（2）如果两班联合起来，作为一个团体购票，可省多少钱？
（3）如果初一（1）班单独组织去游公园，作为组织者的你将如何购票才最省钱？
【考点】一元一次方程的应用．
【专题】经济问题；图表型．
【分析】若设初一（1）班有x人，根据总价钱即可列方程；
第二问利用算术方法即可解答；
第三问应尽量设计的能够享受优惠．
【解答】解：（1）设初一（1）班有x人，
则有13x+11（104﹣x）=1240或13x+9（104﹣x）=1240，
解得：x=48或x=76（不合题意，舍去）．
即初一（1）班48人，初一（2）班56人；
（2）1240﹣104×9=304，
∴可省304元钱；
（3）要想享受优惠，由（1）可知初一（1）班48人，只需多买3张，
51×11=561，48×13=624＞561
∴48人买51人的票可以更省钱．
【点评】在优惠类一类问题中，注意认真理解优惠政策，审题要细心．
【探究篇】
19. （2018•随州）我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式（整数可看作分母为1的分数），那么无限循环小数如何表示为分数形式呢？请看以下示例：
例：将0.化为分数形式
由于0. =0.777…，设x=0.777…①
则10x=7.777…②
②﹣①得9x=7，解得x=，于是得0. =．
同理可得0. = =，1. =1+0. =1+=
根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）
【基础训练】
（1）0. =　　，5. =　　；
（2）将0. 化为分数形式，写出推导过程；
【能力提升】
（3）0. 1=　 　，2.0=　 　；
（注：0. 1=0.315315…，2.0=2.01818…）
【探索发现】
（4）①试比较0.与1的大小：0.　 　1（填“＞”、“＜”或“=”）
②若已知0. 8571=，则3. 1428=　 　．
（注：0. 857l=0.285714285714…）
【分析】根据阅读材料可知，每个整数部分为零的无限循环小数都可以写成分式形式，如果循环节有n位，则这个分数的分母为n个9，分子为循环节．
【解答】解：（1）由题意知0. =、5. =5+=，
故答案为：、；
（2）0. =0.232323……，
设x=0.232323……①，
则100x=23.2323……②，
②﹣①，得：99x=23，
解得：x=，
∴0. =；
（3）同理
0. 1==，2.0=2+=
故答案为：，
（4）①0. = =1
故答案为：=
②3. 1428=3+=3+=
故答案为：
20. 已知数轴上点A与16个单位长度，点A在原点的左侧，到原点的距离为26个单位长度，点B在点A的右侧，点C表示的数与点B表示的数互为相反数，动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．
（1）点A表示的数为___________，点B表示的数为___________，点C表示的数为___________．
（2）用含t的代数式表示P到点A和点C的距离： PA= ，PC=___________．

（3）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动， Q点到达C点后，再立即以同样的速度返回，运动到终点A．
①在点Q向点C运动过程中，能否追上点P?若能，请求出点Q运动几秒追上．


②在点Q开始运动后，P、Q两点之间的距离能否为2个单位？如果能，请求出此时点P表示的数；如果不能，请说明理由．



【答案】（1）-26，-10，10（2）PA=t，PC=36-t（3）-3，-1，，
【解析】（1）根据：数轴上点离为16个单位长度，点A在原点的左侧，到原点的距离为26个单位长度，点B在点A的右侧，点C表示的数与点B表示的数互为相反数，可以确定A、B、C点对应的数；
（2）因为动点P从A出发，以每秒1个单位的速度向终点C移动，且移动时间为t秒，所以PA=t，PC=36-t；
（3）①设运动时间是t秒，根据点Q追上点P时，点Q运动的路程=点P运动的路程，列出关于t的方程，求出方程的解即可得到结果．
②分情况讨论：点Q从A点，又分点Q在点P的后面与点Q在点P的前面；点Q从C点返回到点A时，又分点Q在点P的后面与点Q在点P的前面．
解：（1）根据题意可得：点A表示的数为-26，点B表示的数为-10，点C表示的数为10；
（2）因为动点P从A出发，以每秒1个单位的速度向终点C移动，且移动时间为t秒，所以PA=t，PC=36-t；
（3）①设运动时间是t秒，根据点Q追上点P时，点Q运动的路程=点P运动的路程，列方程得：3t=1×（t+16），解得t=8；
②分两种情况：（Ⅰ）点Q从A点向点C运动时，如果点Q在点P的后面，那么1×（t+16）-3t=2，解得t=7，此时点P表示的数是-3；如果点Q在点P的前面，那么3t-1×（t+16）=2，解得t=9，此时点P表示的数是-1；（Ⅱ）点Q从C点返回到点A时，如果点Q在点P的后面，那么3t+1×（t +16）+2=2×36，解得t=，此时点P表示的数是；如果点Q在点P的前面，那么3 t +1×（t +16）=2×36+2，解得t =，此时点P表示的数是．
答：在点Q开始运动后，P、Q两点之间的距离能为2个单位，此时点P表示的数分别-3，-1，，．