备战中考数学一轮总复习达标检测题 平面直角标系、函数及其图象（解析版）

这是一份备战中考数学一轮总复习达标检测题 平面直角标系、函数及其图象（解析版），共13页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
备战中考数学一轮总复习达标检测题 平面直角标系、函数及其图象
时间：45分钟 满分：100分
一、单选题（共7题，每题4分；共28分）
1．（2017•湘潭）函数y＝中，自变量x的取值范围是（　　）
A．x≥－2 B．x＜－2 C．x≥0 D．x≠－2

2．（2018·咸宁）甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4 分钟，在整个步行过程中，甲 、乙两人的距离y（米）与甲出发的时间t（分）之间的关系如图所示，下列结论：
①甲步行的速度为60米/分； ②乙走完全程用了32分钟；
③乙用 16分钟追上甲； ④乙到达终点时，甲离终点还有300米
其中正确的结论有（ ）

A．1个 B．2个 C．3个 D．4个

3．（2018·抚顺）已知点A的的坐标为（1，3），点B的的坐标为（2，1）．将线段AB沿某一方向平移后点A的对应点的坐标为（－2，1）．则点B的对应点的坐标为（ ）
A.(5,3) B.(-1,-2) C．（－1、－1) D.(0,-1)

4． （2018·贵港）若点A（1＋m，1－n）与点B（－3，2）关于y轴对称，则m＋n的值是（ ）
A．－5 B．－3 C．3 D．1

5．（2018·扬州）在平面直角坐标系的第二象限内有一点M，点M到x轴的距离为3，到y轴的距离为4，则点M的坐标是（ ）
A．（3，－4） B．（4，－3） C．（－4，3） D．（－3，4）
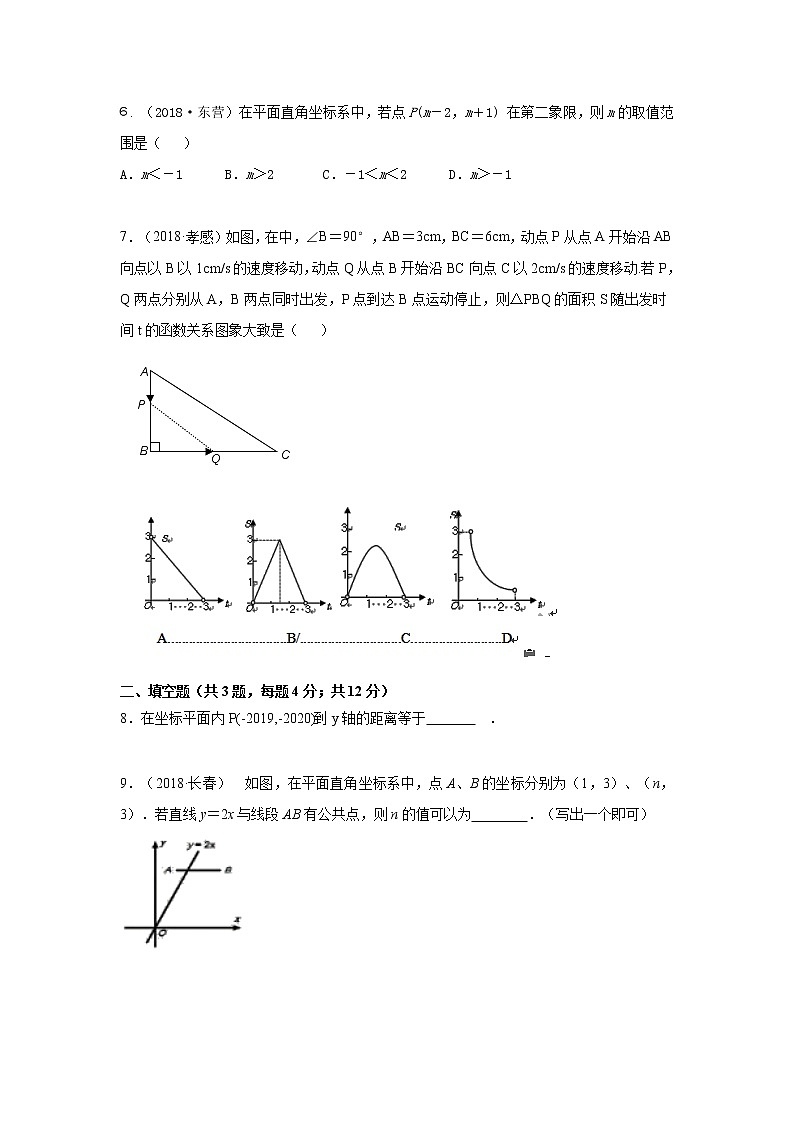
6．（2018·东营）在平面直角坐标系中，若点P(m－2，m＋1) 在第二象限，则m的取值范围是（ ）
A．m＜－1 B．m＞2 C．－1＜m＜2 D．m＞－1

7．（2018·孝感）如图，在中，∠B＝90°，AB＝3cm，BC＝6cm，动点P从点A开始沿AB向点以B以1cm/s的速度移动，动点Q从点B开始沿BC向点C以2cm/s的速度移动.若P，Q两点分别从A，B两点同时出发，P点到达B点运动停止，则△PBQ的面积S随出发时间t的函数关系图象大致是（ ）
A
C
B
P
Q


二、填空题（共3题，每题4分；共12分）
8．在坐标平面内P(-2019,-2020)到y轴的距离等于 　．

9．（2018·长春） 如图，在平面直角坐标系中，点A、B的坐标分别为（1，3）、（n，3）．若直线y＝2x与线段AB有公共点，则n的值可以为 ．（写出一个即可）



10．（2018·咸宁）如图，将正方形OEFG放在平而直角坐标系中，O是坐标原点，点E的坐标为（2,3），则点F的坐标为________．



三、解答题（共6题，每题10分；共60分）
11．已知点P（3m﹣9，m+1），试分别根据下列条件，求出点P的坐标．
（1）点P在y轴上；
（2）点P在x轴上；
（3）点P的纵坐标比横坐标大12；
（4）点P在过点A(﹣2018，8)，且与y轴垂直的直线上．求AP长


12．在平面直角坐标系中,A（0,20）,B在原点,C（26,0）,D(24,20),动点P从A开始沿AD边向D以1cm/s的速度运动,动点从点C开始沿CB以3cm/s的速度向B运动,P、Q同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为ts,问t为何值时：
(1)四边形PQCD是平行四边形?并写出P、Q的坐标；
(2)四边形形PQCD是等腰梯形?并写出P、Q的坐标.

13．(2018·黄石)如图，在Rt△PMN中，∠P＝90°，PM＝PN，MN＝6cm，矩形ABCD中AB＝2cm，BC＝10cm，点C和点M重合，点B、C(M)、N在同一直线上，令Rt△PMN不动，矩形ABCD沿MN所在直线以每秒1cm的速度向右移动，至点C与点N重合为止，设移动x秒后，矩形ABCD与△PMN重叠部分的面积为y， 求y与x的的函数关系式并大致画出其函数图象

14．已知：平面直角坐标系中，已知A（1，0）、
B（﹣2，3）、且C点是由B沿坐标轴向下平移3个单位后再向左平移一个单位得到．
（1）求△ABC的面积是多少？
（2）若点A、C的位置不变，当点P在y轴上时，且S△ACP=4S△ABC，求点P的坐标？
（3）若点B、C的位置不变，当点Q在x轴上时，且S△BCQ=4S△ABC，求点Q的坐标？

15． 在平面直角坐标系xOy中，对于任意两点P1（x1，y1）与P2（x2，y2）的“相对偏差距离”，给出如下定义：若|x1﹣x2|≥|y1﹣y2|，则点P1（x1，y1）与点P2（x2，y2）的“相对偏差距离”为|x1﹣x2|； 若|x1﹣x2||＜|y1﹣y2|，则P1（x1，y1）与点P2（x2，y2）的“相对偏差距离”为|y1﹣y2|；
（1）若M（一2018，2020），N（一2017，2018），则M，N的相对偏差距离为_____
（2）已知点A（﹣2017，0），B为y轴上的动点，
①若点A与B的“相对偏差距离为”2018”，写出满足条件的B点的坐标．
②直接写出点A与点B的“相对偏差距离”的最小值
（3）已知C点坐标为C（m，4m+2017），D（0，2020），求点C与D的“相对偏差距离”的最小值及相应的C点坐标．

16． （2018·无锡）如图，平面直角坐标系中，已知点B的坐标为（6，4）
（1）请用直尺（不带刻度）和圆规作一条直线AC，它与x轴和y轴的正半轴分别交于点A和点C，且使∠ABC=90°，△ABC与△AOC的面积相等．（作图不必写作法，但要保留作图痕迹．）
（2）问：（1）中这样的直线AC是否唯一？若唯一，请说明理由；若不唯一，请在图中画出所有这样的直线AC，并写出与之对应的函数表达式．


备战中考数学一轮总复习达标检测题 平面直角标系、函数及其图象（解析版）
时间：45分钟 满分：100分
一、单选题（共7题，每题4分；共28分）
1．（2017•湘潭）函数y＝中，自变量x的取值范围是（　　）
A．x≥－2 B．x＜－2 C．x≥0 D．x≠－2
【分析】．根据自变量的取值范围，函数关系中主要有二次根式．根据二次根式的意义，被开方数是非负数．
【解答】解：根据题意得：x＋2≥0，解得x≥－2．
故选A．
2．（2018·咸宁）甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4 分钟，在整个步行过程中，甲 、乙两人的距离y（米）与甲出发的时间t（分）之间的关系如图所示，下列结论：
①甲步行的速度为60米/分； ②乙走完全程用了32分钟；
③乙用 16分钟追上甲； ④乙到达终点时，甲离终点还有300米
其中正确的结论有（ ）

A．1个 B．2个 C．3个 D．4个
【分析】．由函数图象进行解答．
【解答】解：由图象知，甲4分钟步行了240米，∴甲步行的速度为＝60（米/分），∴结论①正确；∵乙用了16－4＝12分钟追上甲，乙步行的速度比甲＝20（米/分），∴乙的速度为60＋20＝80米/分，从而结论③不正确；∵甲走完全程需要＝40分钟，乙走完全程需要＝30分钟；∴乙到达终点时，甲用了34分钟，甲还有40－34＝6分钟到达终点，离终点还有60×6＝360米，∴结论②④不正确．
故选A
3．（2018·抚顺）已知点A的的坐标为（1，3），点B的的坐标为（2，1）．将线段AB沿某一方向平移后点A的对应点的坐标为（－2，1）．则点B的对应点的坐标为（ ）
A.(5,3) B.(-1,-2) C．（－1、－1) D.(0,-1)

【分析】根据A点的坐标及对应点的坐标可得线段AB向左平移了3个单位，向下平移了两个单位，然后可得B点对应点的坐标．
【解答】解：点A（1，3）平移后变为（-2，1），所以点A向左平移了3个单位，向下平移了两个单位，将点B（2，1）向左平移了3个单位，向下平移了两个单位得到（-1，-1）
故选C
5． （2018·贵港）若点A（1＋m，1－n）与点B（－3，2）关于y轴对称，则m＋n的值是（ ）
A．－5 B．－3 C．3 D．1
【分析】根据关于y轴对称，横纵坐标变成相反数纵坐标不变转化为方程可得答案．
【解答】解：∵点A（1＋m，1－n）与点B（－3，2）关于y轴对称，∴1＋m＝3，1－n＝2，解得：m＝2，n＝－1，则m＋n的值是：2＋（－1）＝1
故选D
5．（2018·扬州）在平面直角坐标系的第二象限内有一点M，点M到x轴的距离为3，到y轴的距离为4，则点M的坐标是（ ）
A．（3，－4） B．（4，－3） C．（－4，3） D．（－3，4）
【分析】到y轴的距离等于横坐标的绝对值,到x轴的距离等于纵坐标的绝对值可求解
【解答】解：设M的坐标为（x，y），∵点M在第二象限内，则x＜0，y＞0；点M到x轴的距离为3，到y轴的距离为4，∴x＝﹣4，y＝3．
故选C
6．（2018·东营）在平面直角坐标系中，若点P(m－2，m＋1) 在第二象限，则m的取值范围是（ ）
A．m＜－1 B．m＞2 C．－1＜m＜2 D．m＞－1
【分析】由各象限内点的坐标符号特征转化为不等式组求解
【解答】解：由已知得，∴－1＜m＜2
故选C．
7．（2018·孝感）如图，在中，∠B＝90°，AB＝3cm，BC＝6cm，动点P从点A开始沿AB向点以B以1cm/s的速度移动，动点Q从点B开始沿BC向点C以2cm/s的速度移动.若P，Q两点分别从A，B两点同时出发，P点到达B点运动停止，则△PBQ的面积S随出发时间t的函数关系图象大致是（ ）
A
C
B
P
Q

【分析】 本题考查数形结合，根据题意表示出△PBQ的面积S与t的关系式，求出函数解析式后不难得到答案．
【解答】解：
由题意可得：PB=3﹣t，BQ=2t，
则△PBQ的面积S=PB•BQ=（3﹣t）×2t=﹣t2+3t，
故△PBQ的面积S随出发时间t的函数关系图象大致是二次函数图象，开口向下，
答案：C．
二、填空题（共3题，每题4分；共12分）
8．在坐标平面内P(-2019,-2020)到y轴的距离等于 　．
【分析】直接利用坐标平面内点到坐标轴的距离求解．
【解答】由题意得，P(-2019,-2020)到y轴的距离等于横坐标的绝对值即为2019
故答案：2019
9．（2018·长春） 如图，在平面直角坐标系中，点A、B的坐标分别为（1，3）、（n，3）．若直线y＝2x与线段AB有公共点，则n的值可以为 ．（写出一个即可）

【分析】直接用特殊点进行临界分析可求解．
【解答】解：把y＝3代入y＝2x得3＝2x，∴x＝，∴当n≥时，直线y＝2x与线段AB有公共点，∴n的值可以是2．．
故答案：2（答案不唯一，只要不小于即可）．
10．（2018·咸宁）如图，将正方形OEFG放在平而直角坐标系中，O是坐标原点，点E的坐标为（2,3），则点F的坐标为________．

【分析】：过点E作x轴的垂线，垂足为点N，过点F作y轴的垂线FM交EN于点M，交于点H，通过Rt△OEN≌Rt△EFM进行线段长度与坐标值的转化．
【解答】解：过点E作x轴的垂线，垂足为点N，过点F作y轴的垂线FM交EN于点M，交于点H，则∠ONE＝∠EMF＝90°，∴∠OEN＋∠EON＝90°；∵四边形OEFG是正方形，∴OE＝EF，∠OEF＝90°，∴∠OEN＋∠FEM＝90°，∴∠EON＝∠FEM；∴Rt△OEN≌Rt△EFM；∵点E的坐标为（2,3），∴ON＝EM＝2，EN＝FM＝3，∴点F的坐标为（－1,5）．
M
N

故答案：（－1,5）．

三、解答题（共6题，每题10分；共60分）
11．已知点P（3m﹣9，m+1），试分别根据下列条件，求出点P的坐标．
（1）点P在y轴上；
（2）点P在x轴上；
（3）点P的纵坐标比横坐标大12；
（4）点P在过点A(﹣2018，8)，且与y轴垂直的直线上．求AP长
【分析】考查特点点的坐标特征,转化为方程即可求解
【解答】解：(1)依题意，得：3m﹣9=0，解得m=3，∴m+1=3+1=4，
∴点P的坐标为（0，4）；
(2)依题意，得： m+1=0，解得m=﹣1，∴3m﹣9=3×(﹣1)﹣9=﹣12，
∴点P的坐标为（﹣12，0）；

(3)依题意，得：m+1﹣（3m﹣9）=12，则-2m=2,解得m=-1，
∴3m﹣9=3×（-1）﹣9=﹣12，m+1=-1+1=0， ∴点P的坐标为（﹣12，0）；
（4）依题意，得：m+1=8，解得m=7， ∴3m﹣9=3×7﹣9=12，∴点P的坐标为（12，8）
又AP垂直y轴，即AP平行于x轴， ∴AP=|12-（-2018）|=2030
12．在平面直角坐标系中,A（0,20）,B在原点,C（26,0）,D(24,20),动点P从A开始沿AD边向D以1cm/s的速度运动,动点从点C开始沿CB以3cm/s的速度向B运动,P、Q同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为ts,问t为何值时：
(1)四边形PQCD是平行四边形?并写出P、Q的坐标；
(2)四边形形PQCD是等腰梯形?并写出P、Q的坐标.
【分析】(1)利用对平平行且相等的四边形是平行四边形,设元后转化为方程即可求解．
(2)利用梯形定义,作垂直构造全等三角形转化为方程
【解答】解：(1)若PQCD是平行四边形,而由已知A（0,20）,D(24,20),C（26,0）,D(24,20)可得PD∥QC,故只要PD=QC,即PD=AD-AP=24-t QC=3t;∴24-t=3t ∴t=6 P(6,20) Q(8,0)
故当t=6时,有PD=QC,又PD∥QC,则PQCD是平行四边形,综上,当t=6时,PQCD是平行边形形时,此时P(6,20) Q(8,0),
(2)等腰梯形 即不平行的两边相等 ∴PQ=CD 过D向x轴作垂线DF 过P向x轴作垂线PE ,∴,∴CF=QE=2, ∴P、Q两点横坐标差为2
∴t-(26-3t)=2 ∴t=7 P(7,20) Q(5,0)

13．(2018·黄石)如图，在Rt△PMN中，∠P＝90°，PM＝PN，MN＝6cm，矩形ABCD中AB＝2cm，BC＝10cm，点C和点M重合，点B、C(M)、N在同一直线上，令Rt△PMN不动，矩形ABCD沿MN所在直线以每秒1cm的速度向右移动，至点C与点N重合为止，设移动x秒后，矩形ABCD与△PMN重叠部分的面积为y， 求y与x的的函数关系式并大致画出其函数图象


【分析】．先求出两种临界情形,即D在PM或PN上时,分别求得t＝2t＝4.,再分0＜t＜2时，2＜t＜4时，4＜t＜6情形分可求得函数关系式，
【解答】解:当点D位于PM上时，此时t＝2.
当0＜t＜2时，y＝t2；
当点D位于第PN时，此时t＝4.
当2＜t＜4时，y＝2＋2×(t－2)＝2t－2；
当4＜t＜6时，y＝2＋4＋(t－4)2＝(t－4)2＋6.


14．已知：平面直角坐标系中，已知A（1，0）、
B（﹣2，3）、且C点是由B沿坐标轴向下平移3个单位后再向左平移一个单位得到．
（1）求△ABC的面积是多少？
（2）若点A、C的位置不变，当点P在y轴上时，且S△ACP=4S△ABC，求点P的坐标？
（3）若点B、C的位置不变，当点Q在x轴上时，且S△BCQ=4S△ABC，求点Q的坐标？
【分析】利用平移规律和点的坐标值与线段值,利用面积转化为方程求解
【解答】解:（1）∵A（1，0），B（﹣2，3），C（﹣3，0），∴AC=1﹣（﹣3）=1+3=4，点B到AC的距离为3，∴△ABC的面积=×4×3=6；
（2）∵S△ACP=4S△ABC=24，∴以AC为底时，△ACP的高OP＝24×2÷4=12，
点P在y轴正半轴时，P（0，12）；
点P在y轴负半轴时，P（0，﹣12）；
（3）∵S△BCQ=4S△ABC，=24，∴以CQ为底时，△BCQ的高为3，底边CQ=24×2÷3=16，∴点Q在C的左边时，Q（﹣3﹣16，0），即Q（﹣19，0）；
点Q在C的右边时，Q（﹣3+16，0），即Q（13，0）

16． 在平面直角坐标系xOy中，对于任意两点P1（x1，y1）与P2（x2，y2）的“相对偏差距离”，给出如下定义：若|x1﹣x2|≥|y1﹣y2|，则点P1（x1，y1）与点P2（x2，y2）的“相对偏差距离”为|x1﹣x2|； 若|x1﹣x2||＜|y1﹣y2|，则P1（x1，y1）与点P2（x2，y2）的“相对偏差距离”为|y1﹣y2|；
（1）若M（一2018，2020），N（一2017，2018），则M，N的相对偏差距离为_____
（2）已知点A（﹣2017，0），B为y轴上的动点，
①若点A与B的“相对偏差距离为”2018”，写出满足条件的B点的坐标．
②直接写出点A与点B的“相对偏差距离”的最小值
（3）已知C点坐标为C（m，4m+2017），D（0，2020），求点C与D的“相对偏差距离”的最小值及相应的C点坐标．
【分析】以新定义题型考查点的坐标的理解和运用
【解答】解:（1）2
（2）①（0，2018）或（0，﹣2018）；
②“相对偏差距离”的最小值是2017；
（3）|m﹣0|=|4m+2017﹣2020|，
解得m=1或，
当m=1时，“相对偏差距离”为1；当m=时，“相对偏差距离”为.
所以，当m=时，“相对偏差距离”最小值为3/5，此时对应C点的坐标为（，）．

16． （2018·无锡）如图，平面直角坐标系中，已知点B的坐标为（6，4）
（1）请用直尺（不带刻度）和圆规作一条直线AC，它与x轴和y轴的正半轴分别交于点A和点C，且使∠ABC=90°，△ABC与△AOC的面积相等．（作图不必写作法，但要保留作图痕迹．）
（2）问：（1）中这样的直线AC是否唯一？若唯一，请说明理由；若不唯一，请在图中画出所有这样的直线AC，并写出与之对应的函数表达式．

【分析】（1）①当△ABC与△AOC全等且拼成矩形，可通过作垂线构造矩形的方法，也可找OB中点画圆的方法找到AC两点，再作直线AC；②当△ABC与△AOC全等且拼成筝形时，作OB的垂直平分线即可；（2），当△ABC与△AOC全等且拼成筝形时，先借助勾股定理列方程求出OA和OC的长，从而得A、C的坐标，在用待定系数法求AC的解析式；当△ABC与△AOC全等且拼成矩形，直接利用待定系数法求AC得解析式．
【解答】解：（1）方法一：过B作BA⊥x轴于A，过B作BC⊥y轴于C，作直线AC（如答图①）；
方法二：连接OB，作OB的垂直平分线交OB于D，以D为圆心，DO为半径作圆D，交x轴于A，交y轴于C，作直线AC（如答图②）；
方法三：连接OB，作OB的垂直平分线交x轴于A，交y轴于C，作直线AC（如答图③）；


① ②

③ ④

（2）不唯一，①当∵△AOC≌△ABC时，过B作BC⊥y轴于E，过B作BA⊥x轴于F（见答图④），则四边形OEBF是矩形，∴OE=6，OF=4，设OA=a，则AE=6-a，∵OA=BA=a，AB2=AE2+BE2 ，∴a2=（6-a）2+42，解得a=，∴A（，0）；同法，设OC=c，CF=c-4， ∵CO=CB=c，CB2=CF2+BF2， ∴c2=（c-4）2+62，解得c=，∴C（0，），设AC解析式为y=kx+b，把A（，0）、C（0，），代入得，解得，∴AC得表达式为；②当∵△AOC≌△CBA时（见答图①），可得∴OA=6，OB=4，点A的坐标为（6，0），C（0，4），设AC解析式为y=kx+b，把A、C代入得，解得，∴AC得表达式为