二次函数与几何综合学案

这是一份二次函数与几何综合学案，共9页。学案主要包含了参考答案等内容，欢迎下载使用。
课前预习
如图，直线 y  1 x 1 经过点 A(1，m)，B(4，n)，点 C 的坐
2
标为(2，5)，则△ABC 的面积为 ．
y
C
B
A
O
x
提示：利用点坐标求面积，需要将点坐标转化为横平竖直的线段长，常考虑作横平竖直的线来对图形进行割补．
具体操作：
①过点 C 作 CD∥y 轴，交 AB 于点 D；
②借助 C，D 坐标求解 CD 长；
③以 CD 为底，则 A，B 两点间的水平距离为高，即
S△ ABC
 S△ ADC
S△DBC
 1  CD  (x
2
B  xA ) ．
如图，在平面直角坐标系 xOy 中，直线 y   3 x  3与 x 轴，
4
y
B
O
A
x
C
y 轴分别交于点 A，B，点 C 的坐标为(0，-2)．若点 D 在直线 AB 上运动，点 E 在直线 AC 上运动，当以 O，A，D，E 为顶点的四边形是平行四边形时，点D 的坐标为 ．
提示：
（1）分析定点（A，O），动点（D，E），属于两定两动的平行四边形存在性问题．
（2）连接两定点得定线段，考虑：①若定线段作为平行四边形的边，则通过平移确定点的坐标；②若定线段作为平行四边形的对角线，则绕定线段中点旋转，利用中点坐标公式确定点的坐标．
（3）利用函数特征和几何特征求解后，结合图形进行验证．
知识点睛
“函数与几何综合”问题的处理原则： ，
．
研究背景图形：
①研究函数表达式．二次函数关注 ，一次函数 关注 ．
② ．找特殊图形、特殊位置关 系，寻求边长和角度信息．
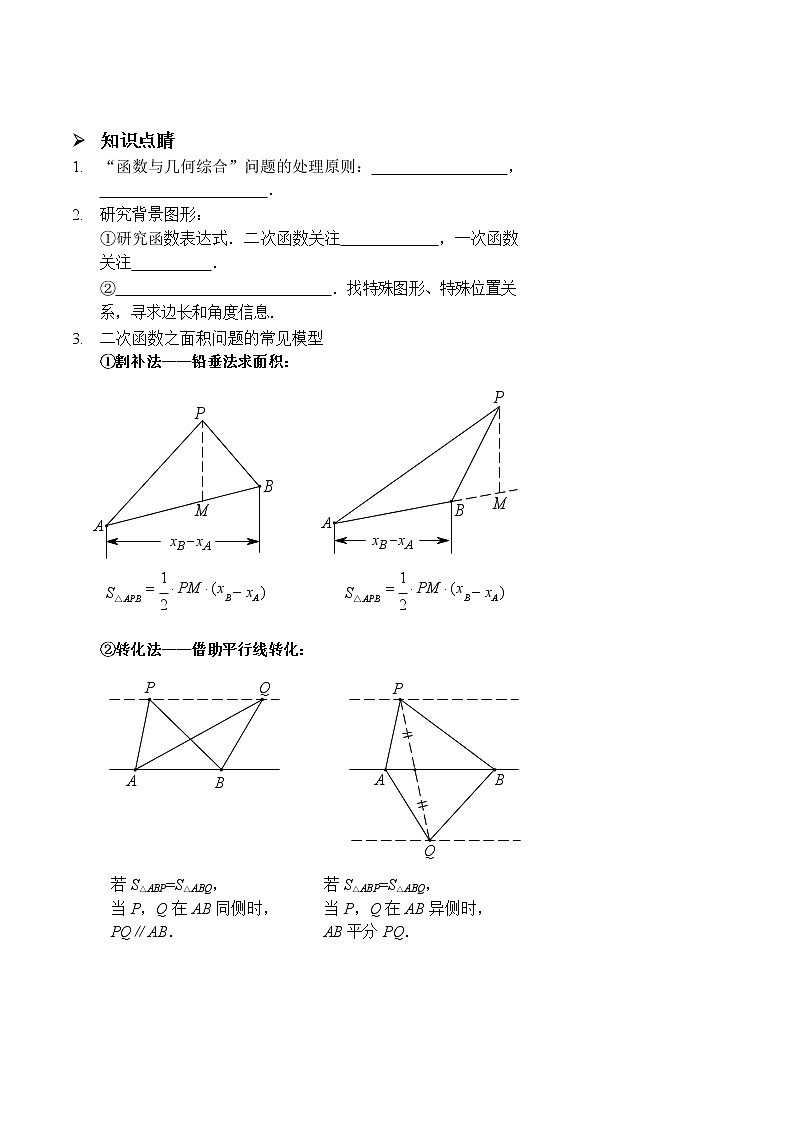
二次函数之面积问题的常见模型
①割补法——铅垂法求面积：
P
B
M
xB xA
M
xB xA
P
B
AA
S△ APB
 1  PM  (x
2
B  xA )
S△ APB
 1  PM  (x
2
B  xA )
②转化法——借助平行线转化：
A
B
PQP
AB
Q
若 S△ABP=S△ABQ，若 S△ABP=S△ABQ，
当 P，Q 在 AB 同侧时，当 P，Q 在 AB 异侧时，
PQ∥AB．AB 平分 PQ．
精讲精练
如图，抛物线 y=-x2+2x+3 经过 A，B，C 三点．点 M 是直线
BC 上方抛物线上的点（不与 B，C 重合），过点 M 作 MN∥y
轴交线段 BC 于点 N，连接 MB，MC．
（1）若设点 M 的横坐标为 m，四边形 OBMC 的面积为 S， 则 S 与 m 的函数关系式为 ．
（2）四边形 OBMC 的最大面积为 ，此时点 M 的坐标为 ．
y
M
C
N
AO
B
x
y
M
C
N
AO
B
x
y
M
C
N
AO
B
x
如图，在平面直角坐标系中，抛物线 y=-x2+2x+3 经过 A，B，
C 三点，点 D 的坐标为(0，1)，直线 AD 与抛物线交于另一点E．
（1）若 M 是直线 AD 上方抛物线上的一个动点，则△AME 面积的最大值为 ．
y
C
E
A
D
O
B
x
y
C
E
A
D
O
B
x
y
C
E
A
D
O
B
x
（2）在直线 AD 下方的抛物线上有一动点 G，当 S△AEG=6 时， 点 G 的坐标为 ．
如图，已知抛物线 y=ax2-2ax-b（a＞0）与 x 轴交于 A，B 两点，点 A 在点 B 的右侧，且点 B 的坐标为(-1，0)，与 y 轴的负半轴交于点 C，顶点为 D．连接 AC，CD，∠ACD=90°．
（1）直接写出抛物线的解析式；
（2）若点 M 在抛物线上，且以点 M，A，C 以及另一点 N 为顶点的平行四边形 ACNM 的面积为 12，设 M 的横坐标为 m， 求 m 的值．
y
B O
A
x
C
D
y
B O
A
x
C
D
y
B O
A
x
C
D
如图，已知二次函数 y=x2-3x-4 的图象与 x 轴交于点 A，B， 且经过点 C(2，-6)，连接 AC，二次函数图象的对称轴记为 l．
（1）点 D(m，n)（-1＜m＜2）是二次函数图象上一动点，当
△ACD 的面积为 27 时，点 D 关于 l 的对称点为 E，求点 E
8
的坐标．
y
l
A
B
Ox
D
C
y
l
A
B
Ox
D
C
y
l
A
B
Ox
D
C
（2）在（1）的条件下，能否在二次函数图象和直线 l 上分别找到点 P，Q，使得以点 D，E，P，Q 为顶点的四边形为平行四边形．若能，求出点 P 的坐标；若不能，请说明理由．
如图，抛物线 y=ax2-5ax+4（a＜0）经过△ABC 的三个顶点， 已知 BC∥x 轴，点 A 在 x 轴上，点 C 在 y 轴上，且 AC=BC．
（1）求抛物线的解析式；
（2）已知点 D 在抛物线对称轴上，点 E 在抛物线上，且以 A，
B，D，E 为顶点的四边形是平行四边形，求点 E 的坐标；
（3）已知点 F 是抛物线上的动点，点 G 是直线 y=-x 上的动点，且以 O，C，F，G 为顶点的四边形是平行四边形，求点
y
C
B
A
O
x
y
C
B
A
O
x
G 的横坐标．
y
C
A
O
x
y
C
A
O
x
【参考答案】
课前预习
知识点睛
利用横平竖直的线段长，函数特征与几何特征互转
①四点一线；k，b
②坐标转线段长
精讲精练