七年级上册角度的存在性练习（有答案）

这是一份七年级上册角度的存在性练习（有答案），共7页。
例题示范
先填写思路分析；再对比过程示范
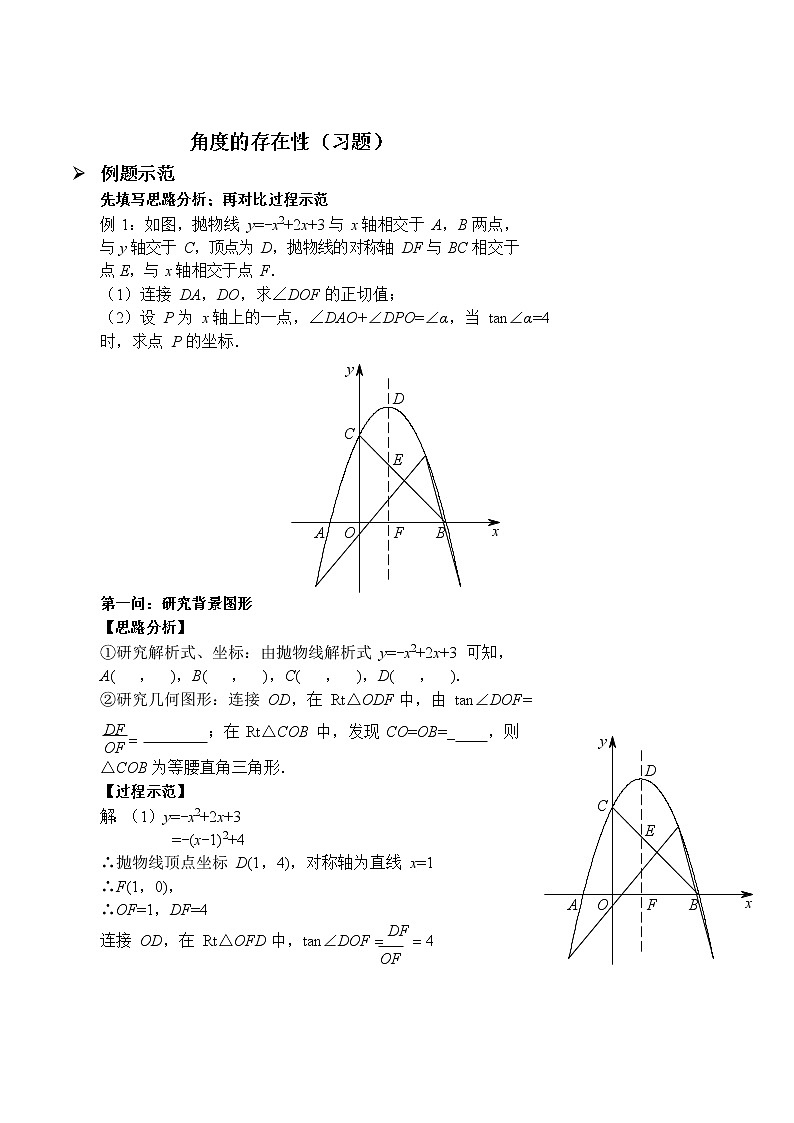
例 1：如图，抛物线 y=-x2+2x+3 与 x 轴相交于 A，B 两点， 与 y 轴交于 C，顶点为 D，抛物线的对称轴 DF 与 BC 相交于点 E，与 x 轴相交于点 F．
（1）连接 DA，DO，求∠DOF 的正切值；
（2）设 P 为 x 轴上的一点，∠DAO+∠DPO=∠α，当 tan∠α=4
y
D
C
E
AO
F
B
x
时，求点 P 的坐标．
第一问：研究背景图形
【思路分析】
①研究解析式、坐标：由抛物线解析式 y=-x2+2x+3 可知，
A(，)，B(，)，C(，)，D(，).
y
D
C
E
AO
F
B
x
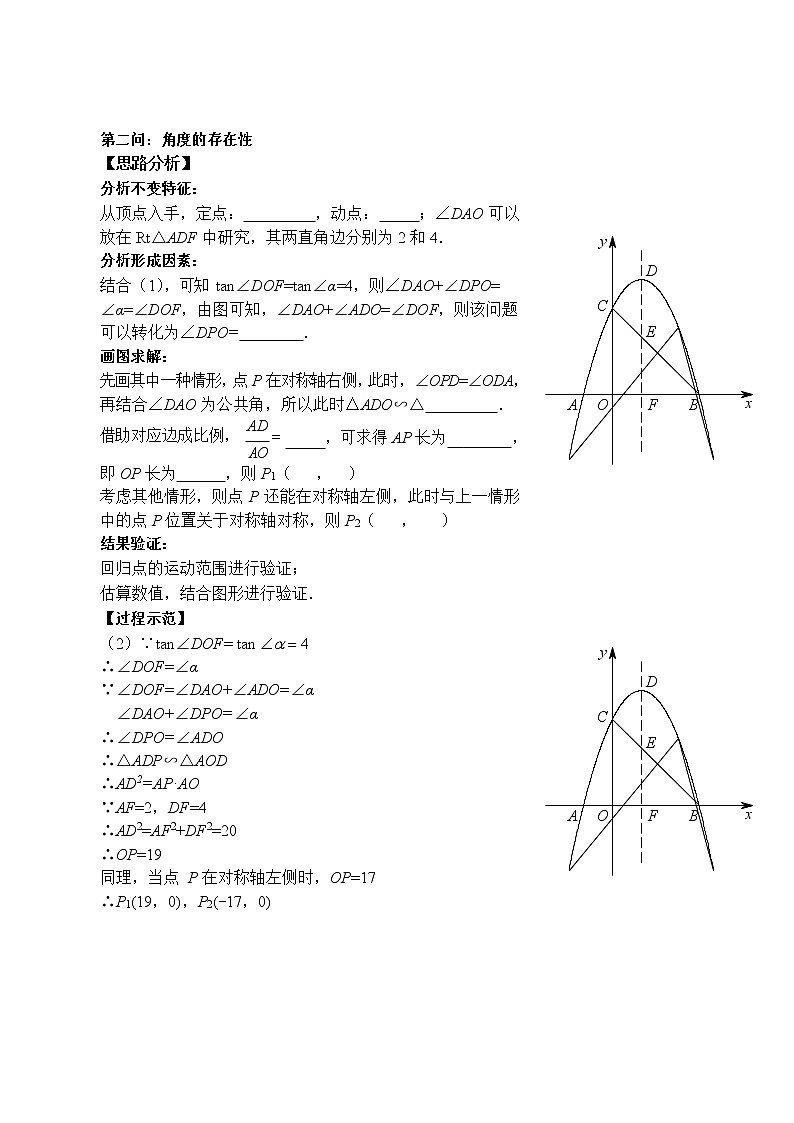
②研究几何图形：连接 OD，在 Rt△ODF 中，由 tan∠DOF=
DF 
OF
；在 Rt△COB 中，发现 CO=OB=_，则
△COB 为等腰直角三角形．
【过程示范】
解：（1）y=-x2+2x+3
=-(x-1)2+4
∴抛物线顶点坐标 D(1，4)，对称轴为直线 x=1
∴F(1，0)，
∴OF=1，DF=4
连接 OD，在 Rt△OFD 中，tan∠DOF  DF  4
OF
第二问：角度的存在性
【思路分析】 分析不变特征：
y
D
C
E
AO
F
B
x
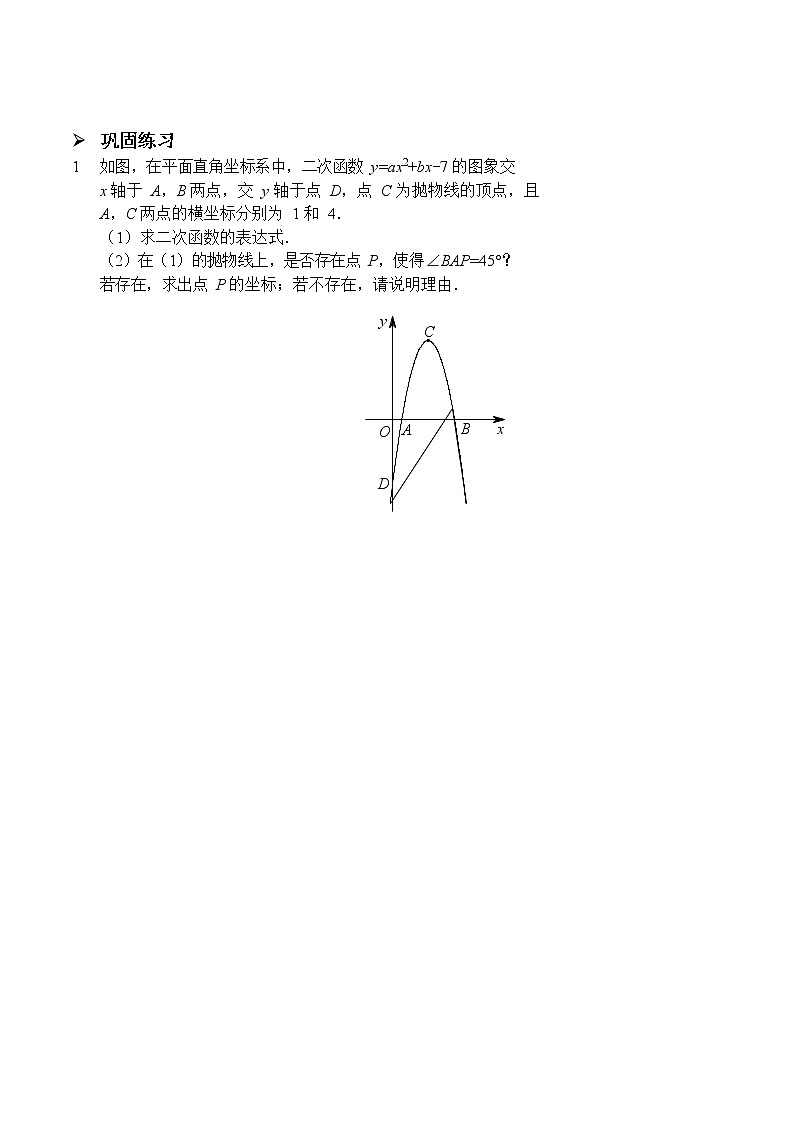
从顶点入手，定点： ，动点： ；∠DAO 可以放在 Rt△ADF 中研究，其两直角边分别为 2 和 4．
分析形成因素：
结合（1），可知 tan∠DOF=tan∠α=4，则∠DAO+∠DPO=
∠α=∠DOF，由图可知，∠DAO+∠ADO=∠DOF，则该问题可以转化为∠DPO= ．
画图求解：
先画其中一种情形，点 P 在对称轴右侧，此时，∠OPD=∠ODA， 再结合∠DAO 为公共角，所以此时△ADO∽△ ．
借助对应边成比例， AD 
AO
，可求得 AP 长为，
即 OP 长为 ，则 P1（，）
考虑其他情形，则点 P 还能在对称轴左侧，此时与上一情形中的点 P 位置关于对称轴对称，则 P2（，）
结果验证：
回归点的运动范围进行验证； 估算数值，结合图形进行验证．
【过程示范】
y
D
C
E
AO
F
B
x
（2）∵tan∠DOF= tan   4
∴∠DOF=∠α
∵∠DOF=∠DAO+∠ADO=∠α
∠DAO+∠DPO=∠α
∴∠DPO=∠ADO
∴△ADP∽△AOD
∴AD2=AP·AO
∵AF=2，DF=4
∴AD2=AF2+DF2=20
∴OP=19
同理，当点 P 在对称轴左侧时，OP=17
∴P1(19，0)，P2(-17，0)
巩固练习
如图，在平面直角坐标系中，二次函数 y=ax2+bx-7 的图象交
x 轴于 A，B 两点，交 y 轴于点 D，点 C 为抛物线的顶点，且
A，C 两点的横坐标分别为 1 和 4．
（1）求二次函数的表达式．
（2）在（1）的抛物线上，是否存在点 P，使得∠BAP=45°？ 若存在，求出点 P 的坐标；若不存在，请说明理由．
y
C
O A
Bx
D
如图，在平面直角坐标系 xOy 中，顶点为 M 的抛物线是由抛物线 y=x2-3 向右平移 1 个单位后得到的，它与 y 轴负半轴交于点 A，点 B 在该抛物线上，且横坐标为 3．连接 AB，AM， BM，点 P 是抛物线上一点，且位于对称轴的右侧，设 PO 与
x 正半轴的夹角为 α，当 α=∠ABM 时，求点 P 的坐标．
y
B
O
x
P
A
M
如图，已知抛物线 y=ax2+bx+c 与 x 轴交于点 A，B，与直线AC：y=-x-6 交 y 轴于点 C，点 D 是抛物线的顶点，且横坐标为-2．
（1）求出抛物线的解析式．
（2）判断△ACD 的形状，并说明理由．
（3）直线 AD 交 y 轴于点 F，在线段 AD 上是否存在一点 P， 使得∠ADC=∠PCF？若存在，直接写出点 P 的坐标；若不存在，说明理由．
y
A
O
B
x
P
C
D
F
如图，抛物线 y=-x2+2x+3 与 x 轴交于 A，B 两点（点 A 在点
B 的左侧），与 y 轴交于点 C，点 D 为顶点，连接 CD．若 P为抛物线上一个动点，过 P 作 PQ⊥CD 交直线 CD 于点 Q， 使∠CPQ=∠ACO，求点 P 的坐标．
y
D
C
A
O
Bx
思考小结
回顾角度存在性的处理流程分析不变特征：
从顶点入手，分析定点、动点，确定所求角度的信息（正切值）．
分析形成因素：
找构成角的两条射线，判断是否有固定的射线；根据角是由两条具有公共端点的射线组成，只需找到另一条射线所在直线即可．
画图，求解：
结合角度常放到直角三角形中处理，考虑从固定射线上的已知点（定点）为直角顶点构造直角三角形，将所求角放到直角三角形中，借助斜直角的用法，构造三等角模型，表达线段长、坐标，求直线解析式．
结果验证：
回归点的运动范围进行验证； 估算数值，结合图形进行验证．
【参考答案】
例题示范
第一问【思路分析】①A(-1，0)，B(3，0)，C(0，3)，
D(1，4)
②4；3
第二问【思路分析】分析不变特征：A，D，O；P； 分析形成因素：∠ADO
画图求解：AP1D； AP1 ；20；19；P1(19，0)；P2(-17，0)
AD