2020-2021学年1.1 集合的概念教案设计

这是一份2020-2021学年1.1 集合的概念教案设计，共4页。教案主要包含了 集合，元素，元素与集合的关系等内容，欢迎下载使用。


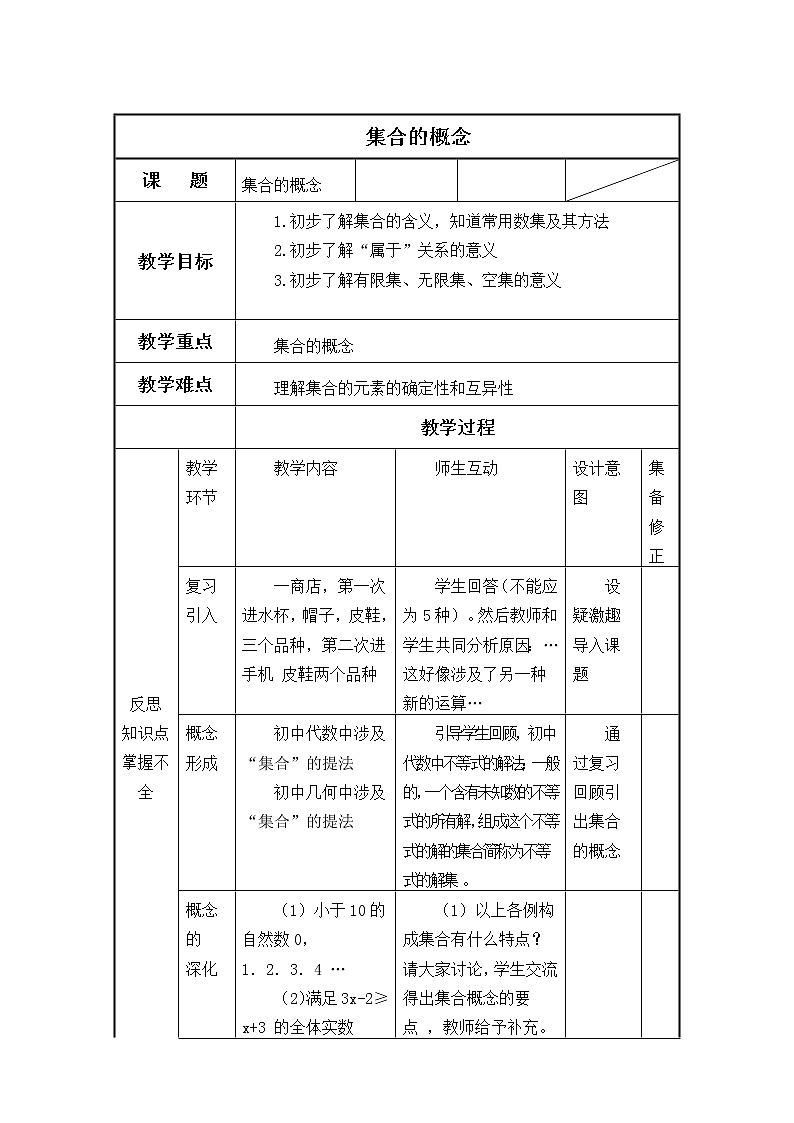
集合的概念
课 题
集合的概念
教学目标
1.初步了解集合的含义，知道常用数集及其方法
2.初步了解“属于”关系的意义
3.初步了解有限集、无限集、空集的意义
教学重点
集合的概念
教学难点
理解集合的元素的确定性和互异性
教学过程
反思
知识点掌握不全
教学环节
教学内容
师生互动
设计意图
集备修正
复习引入
一商店，第一次进水杯，帽子，皮鞋，三个品种，第二次进手机 皮鞋两个品种
学生回答（不能应为5种）。然后教师和学生共同分析原因：…这好像涉及了另一种新的运算…
设疑激趣导入课题
概念形成
初中代数中涉及“集合”的提法
初中几何中涉及“集合”的提法
引导学生回顾，初中代数中不等式的解法：一般的，一个含有未知数的不等式的所有解，组成这个不等式的解的集合简称为不等式的解集 。
通过复习回顾引出集合的概念
概念的
深化
（1）小于10的自然数0，1．2．3．4 …
（2）满足3x-2≥ x+3 的全体实数
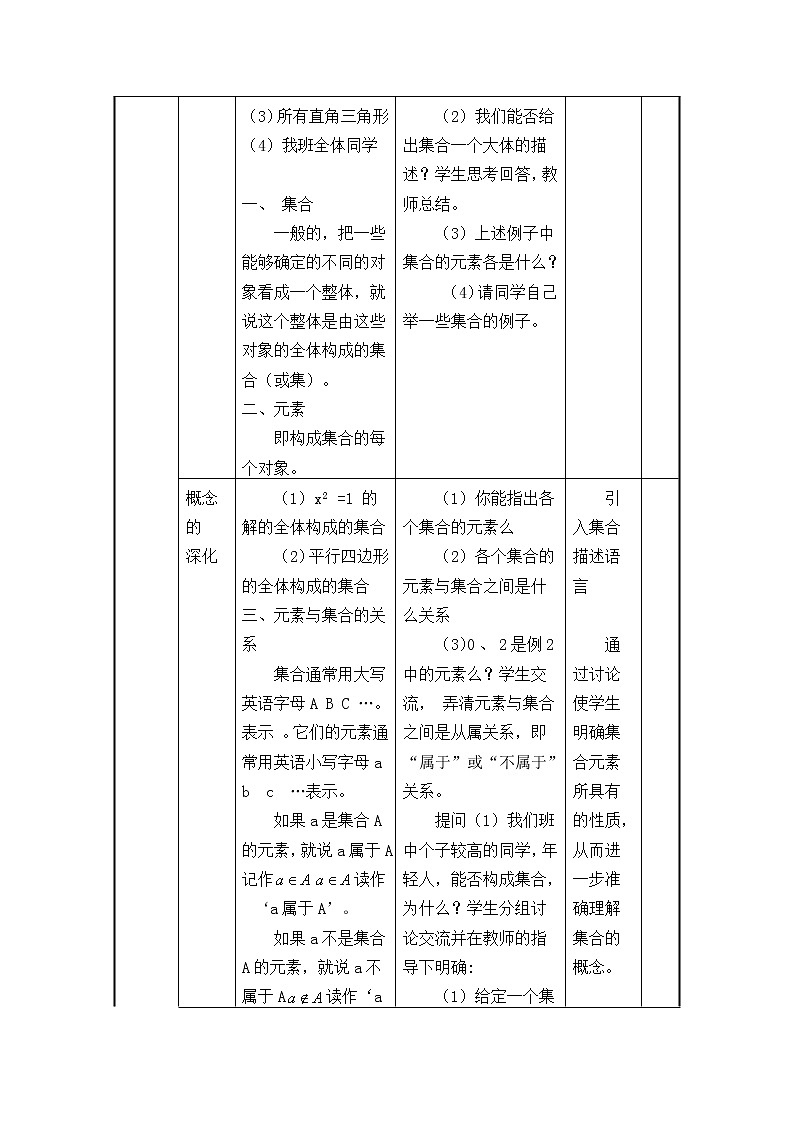
（3）所有直角三角形
（4）我班全体同学
一、 集合
一般的，把一些能够确定的不同的对象看成一个整体，就说这个整体是由这些对象的全体构成的集合（或集）。
二、元素
即构成集合的每个对象。
（1）以上各例构成集合有什么特点？请大家讨论，学生交流得出集合概念的要点 ，教师给予补充。
（2）我们能否给出集合一个大体的描述？学生思考回答，教师总结。
（3）上述例子中集合的元素各是什么？
（4）请同学自己举一些集合的例子。
概念的
深化
（1）x2 =1 的解的全体构成的集合
（2）平行四边形的全体构成的集合
三、元素与集合的关系
集合通常用大写英语字母A B C …。表示 。它们的元素通常用英语小写字母a b c …表示。
如果a是集合A的元素，就说a属于A 记作读作‘a属于A’。
如果a不是集合A的元素，就说a不属于A读作‘a不属于A’
集合的元素的基本性质：
1. 确定性
2. 互异性
3.无序性
（1）你能指出各个集合的元素么
（2）各个集合的元素与集合之间是什么关系
（3）0 、 2 是例2中的元素么？学生交流， 弄清元素与集合之间是从属关系，即“属于”或“不属于”关系。
提问（1）我们班中个子较高的同学，年轻人，能否构成集合，为什么？学生分组讨论交流并在教师的指导下明确:
（1）给定一个集合，任何一个对象是不是这个集合中的元素也就确定了。
（2）集合的对象一定是互异的，相同的对象归于同一个集合中只能算作集合的一个元素。
引入集合描述语言
通过讨论使学生明确集合元素所具有的性质，从而进一步准确理解集合的概念。
x2 ， 3x+1 ，
2 x2 –x +5 三个式子构成的集合。
x2≥0构成的集合。
x2= -1 的全体实数构成的集合。
空集 ：不含任何元素的集合。记作 。
集合的分类 ：按所含元素的个数分为 有限集和无限极。
他们各有多少个元素？学生通过思考回答问题。
然后依据元素个数的多少将集合分类。
通过实例发现集合元素具有不同的类别，从而使学生感受到有限集， 无限极 ，空集存在的客观意义。
应用举例
常用数集及其记号。
N 非负整数集（自然数集）
Z 整数集
Q 有理数集
R实数集
请同学们熟记上述符号。
归纳总结
例一 已知由 1． x ，x2
三个实数构成一个集合，求x应满足的条件。
解：x1 x21 x2 x
所以 且
学生分析求解 教师板书。
通过应用 ，进一步理解集合的有关概念。
板书设计
一、 概念 二、集合的分类 例题
1．实例引入 特殊集合的记号
2．集合的概念
3．元素与集合关系表示
4．元素的特征