





2022年九年级中考二轮总复习·数学 专题三 新定义型问题 课件
展开“新定义”型问题,是指命题者用下定义的方式,在问题中定义了一些没有学过的新的运算、符号、概念、图形或性质等,要求答题者“化生为熟”、“现学现用”,能结合已有知识、能力进行理解,进而进行运算、推理、迁移的一种题型。这类题型往往是教材中一些数学概念的拓展、变式。
解决此类问题的方法,就是要认真阅读材料,把握题意,注意一些例子、关键名词、符号、规则等,了解新定义所代表的意义,并将它转化成熟悉的知识,而后利用已有的知识经验来解决问题。“遮遮掩掩似新人,揭去面纱是故友”。
这类问题是以加、减、乘、除、乘方、开方等运算为基础,定义了很多新运算。实质是给出了一种新符号、新法则,以此考查学生的思维应变能力和演算能力。解这种题的关键是深刻理解所给的定义和规则,将它们转化成我们熟悉的运算。 “新定义,旧运算”。
考点1 代数类新定义型问题
对于任意实数a、b,a ♢ b=2a+b。例如3 ♢4=2 ×3+4=10.
(1)求2 ♢(-5)的值;
(2)已知x ♢(-y)=2,且2y ♢x=-1,求 x + y 的值.
=2 × 2+(-5)=-1
(2)∵x ♢(-y)=2 且 2y ♢x=-1
∴2x +(-y)=2 且 2×2y +x=-1
①+②得3x+3y=1
【感悟】理解算理算法是关键.
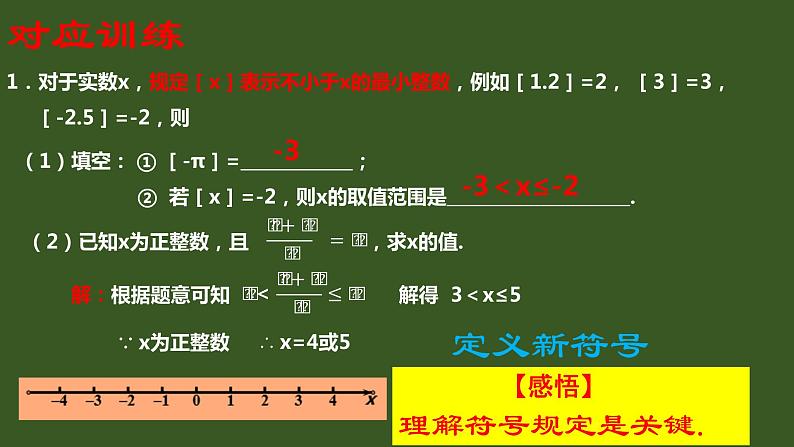
1.对于实数x,规定[x]表示不小于x的最小整数,例如[1.2]=2, [3]=3, [-2.5]=-2,则
(1)填空: ① [-π]= ; ② 若[x]=-2,则x的取值范围是 .
【感悟】理解符号规定是关键.
3.定义运算“※”为:a ※ b=a × b-(a+b) ,则
(1)填空: ① 5※7 = , 7※5 = ; ② 12※(3※4) = , (12※3) ※4 = .
(2)“※”这个运算 交换律,“※”这个运算 结合律. (填“有”或“没有”)
(3)如果3※(5 ※ x)=3,求x的值.
5※x =5x-(5+x)=5x-5-x=4x-5
∵ 3※(5 ※ x)=3
∴ 3※(4x-5) =3
∴ 3(4x-5)-[3+(4x-5)] =3
∴ 12x-15-3-4x+5=3
4.我们知道,一元二次方程x2=-1没有实数根,即不存在一个实数的平方等于-1,若 我们规定一个新数“i”,使其满足i2=-1(即方程x2=-1有一个根为i),并且进一步 规定:一切实数可以与新数进行四则运算,且原有的运算律和运算法则仍然成立, 于是有 i1=i,i2=-1, i3= i2 · i=(-1) · i= -i, i4=(i2)2 =(-1)2=1,从而 对任意正整数n,我们可以得到i4n+1= i4n · i =(i4)n · i= i,同理可得i4n+2=-1, i4n+3=-i, i4n=1,那么i+i2+i3+i4+ … +i2015+i2016的值为( ) A. 0 B. 1 C. -1 D. I
i+i2+i3+i4 =i+(-1)+(-i)+1=0
2016 ÷4=504
(1)有括号时,应先算括号里的;
(2)新定义的运算不一定具备交换律和结合律,不能随便套用这些 运算律来解题;
(3)符号 ♢ ,※,△ ,● ,☆ …… 所表示的运算并不是一种固定的 算法,而是因题而异,不同的题目有不同的规定,我们应当严格 按不同的规定进行运算。
在近年的中考试题中,涌现出了许多创意新颖、情境熟悉的几何新定义型试题。有的定义一个新点(准外心、关联点、黄金分割点等),有的定义一个新线段(中对线、黄金分割线等),有的定义一个新三角形(好玩三角形、叠弦三角形、曲边三角形等)、有的定义一个新四边形(垂美四边形、友好矩形、等邻边四边形、黄金矩形、曲边梯形等)、有的定义一个新几何体(相似体等)。共同特点就是给出新定义,提出新问题,通过实验、探究、猜想,在新定义下解决新几何问题。
考点2 几何类新定义型问题
如图1,将△ABC纸片沿中位线EH折叠,使点A的对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形.类似地,对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作 形成的折痕分别是线段_____,_____;S矩形AEFG:S□ABCD =______.
∴S矩形AEFG:S□ABCD
由折叠的轴对称性质,得AD=2AG.
∵S矩形AEFG=AE·AG,S□ABCD=AE·AD
=(AE·AG): (AE·AD)
也可以用对称性直接说1:2.
(2) □ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5, EH=12,求AD的长.
由折叠的轴对称性质可知
∴AD=AH+HD=FC+HN=FN+HN=FH
∵四边形ABCD是平行四边形
∴AD∥BC,∠A=∠C
∴△AEH≌△CGF(AAS)
∵四边形EFGH是叠合矩形
HD=HN,FC=FN
又∵ Rt ∆FEH中
(3)如图4,四边形ABCD纸片满足AD∥BC,AD
∴HG=BE=EH=BG=4
∴由勾股定理得 CG=3
∴BF=BG-FG=1
BC=BG+CG=4+3=7
定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线. (1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点. 求证:四边形ABEF是邻余四边形。
∴四边形ABEF是邻余四边形
∵AB=AC,AD是△ABC的角平分线
∴∠DAB+∠B=90°
(2)如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的邻余四边形ABEF, 使AB是邻余线,E,F在格点上。
开放性的命题,答案不唯一:
在过点A的水平线与过点B的竖直线(或过点A的竖直线与过点B的水平线)上各取一个格点F、E,再顺次连接A、F、E、B。即可得出所求的邻余四边形。
(3)如图3,在(1)的条件下,取EF中点M,连结DM并延长交AB于点Q,延长EF交AC于点N。 若N为AC的中点,DE=2BE,QB=3,求邻余线AB的长。
∵AB=AC,AD是△ABC的角平分线
∴CE=CD+DE=5BE
∵由(1)可知∠ADB=90°
这类问题常常以代数几何综合题的形式出现, 其解题关键点是借助几何直观解题, 运用方程、 函数的思想解题,灵活运用数形结合,由形导数,以数促形,综合运用代数和几何知识解题.
考点3 综合类新定义型问题
定义:如果两条线段 相等,且它们所在的直线互相垂直,我们称这样的两条线段为“垂等线段”.
(1)在平面直角坐标系中,点A(0,4)、B(3,0),如果线段AB与线段BC是“垂等线段” 则C点坐标为 ;
(7,3)或(-1,-3)
把线段BA绕点B顺时针旋转90°得点C1,逆时针旋转90°得点C2.
(2)抛物线y=(x-1)(ax-2) 与y轴交于点A(0,2),与x轴交于点B(1,0)和点C.
① 当a=1时,如图,点D的坐标为(m,4),在抛物线上存在点E使得线段DE与线段AB为“垂等线段”, 求m的值;
分别过点D、E作y轴、x轴的平行线交于点F,
∴EF=AO=2,FD=OB=1
如图,当点E在点D下方时
当a=1时, y=(x-1)(ax-2) =(x-1)(x-2)=x2-3x+2
代入 y=x2-3x+2中
如图,当点E在点D上方时
同理得点E的坐标为(m+2,5)
② 点P为平面直角坐标系内的一点,在抛物线上是否存在点Q,使得线段PQ与线段AB为“垂等线段”, 且它们互相平分,若存在,直接写出a的值,若不存在,请说明理由.
∵线段PQ与线段AB为“垂等线段”且它们互相平分
∴如图,四边形APBQ为正方形
过Q作QD⊥x轴,过A作AE⊥QD,垂足分别为D、E
设BD=EQ=b,QD=AE=c
代入y=(x-1)(ax-2) 中
如果P、Q两点位置交换,依然符合题目要求,此时
(1)深刻理解“新定义”,明确“新定义”的条件、原理、方法、步骤 和结论,尽可能把文字语言转化为图形语言,且注意各种可能的图 形分类;
(2)揭示新概念的本质,重视“举例”,利用“举例”检验是否理解和正 确运用“新定义”,归纳“举例”提供的做题方法及分类情况;
(3)依据“新定义”,运用类比、归纳、联想、分类讨论以及数形结合的 数学思想方法解决题目中的问题;
(4)准确画图能起到事半功倍的效果。
新定义型问题热点 —函数及图象
③ 画界线,分区域;
④ 分区域讨论,定“较小值函数”解析式及图象.
① 在同一个平面直角坐标系中分别画出函数y1、y2的图象;
① 在如图的平面直角坐标系中画出函数y的图象;
② 写出函数y的两条性质;
① 函数y的图象如图所示.
② 函数y的两条性质:
当x=1时,函数有最大值;
在每个象限内,随着x的增大,函数y的值先增大后减小.
又∵这部分图象只有在x=1或x=-1时,才有y=0
x=a在x=-1和x=1之间.
这部分图象又是以y轴为分界线的,所以还有界线x=0.
综上,直线x=a只能在①②③三个区域。
符合“当a取某个范围内的任意值时,b为定值”.
不符合“当a取某个范围内的任意值时,b为定值”.
∵ m为常数,且m≠0
∴分m>0和m<0两种情况讨论 .
函数y1 =x2-2mx的对称轴为x=m
随着x的增大,函数y的值也增大.
随着x的增大,函数y的值先增大后减小.
也符合讨论的前提条件m>0
第二种情况:m < 0时
随着x的增大,函数y的值减少.
也符合讨论的前提条件m < 0
中考数学总复习专题五综合型问题课件: 这是一份中考数学总复习专题五综合型问题课件,共36页。PPT课件主要包含了A1个,B2个,C3个,D4个,答案C,解1-2,∴y1=x-3,等腰三角形,∴t=,则AM=等内容,欢迎下载使用。
中考总复习数学 专题 2 新定义型问题课件: 这是一份中考总复习数学 专题 2 新定义型问题课件,共25页。PPT课件主要包含了专题解析,典型例析,·1·,强化训练,·2·,·3·,·4·,·5·,·6·,·7·等内容,欢迎下载使用。
初中数学中考复习 专题6 新定义与阅读理解型问题课件PPT: 这是一份初中数学中考复习 专题6 新定义与阅读理解型问题课件PPT,共37页。PPT课件主要包含了专题解读,精讲释疑等内容,欢迎下载使用。












