2022年中考数学专题复习 阴影部分面积的计算 课件

这是一份2022年中考数学专题复习 阴影部分面积的计算 课件，共34页。PPT课件主要包含了预学问题反馈，探究活动一，探究活动二，间接求---变换法，迁移运用，练习1图，中考真题，练习2图，练习3图，练习4图等内容，欢迎下载使用。

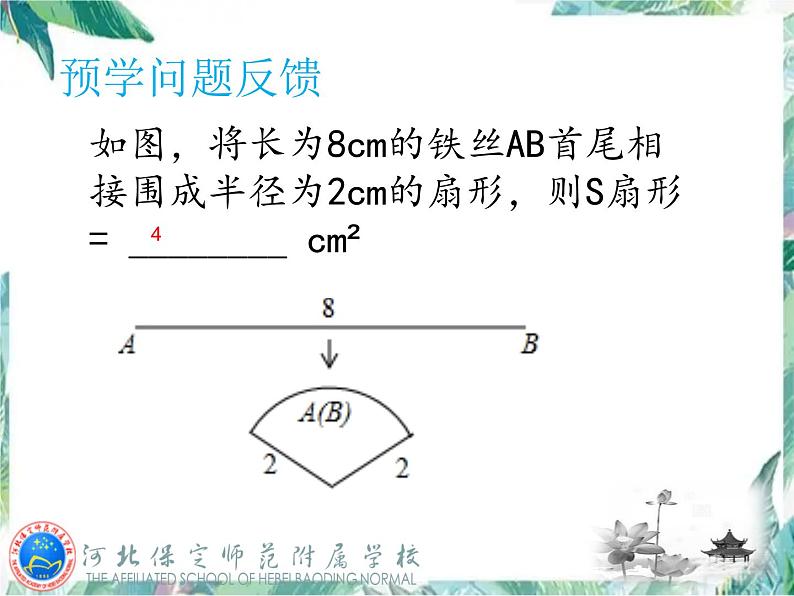
如图，将长为8cm的铁丝AB首尾相接围成半径为2cm的扇形，则S扇形= ________ cm²
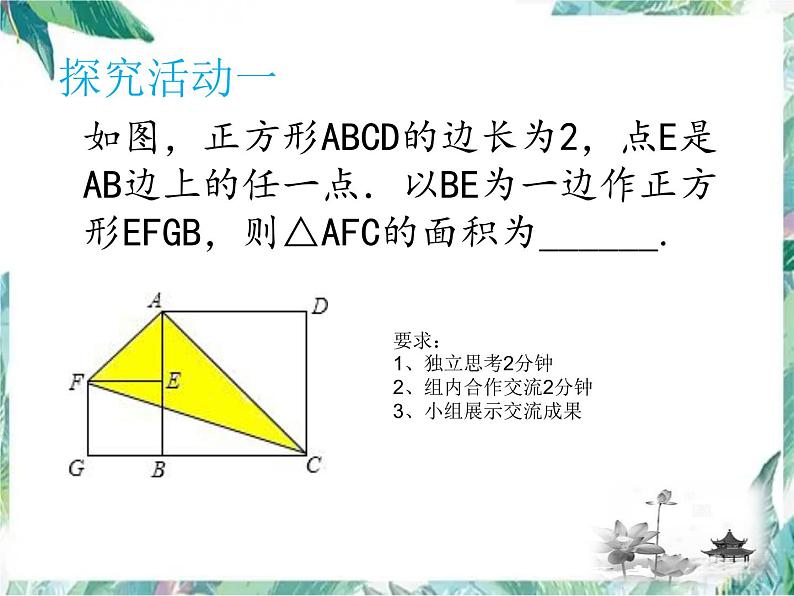
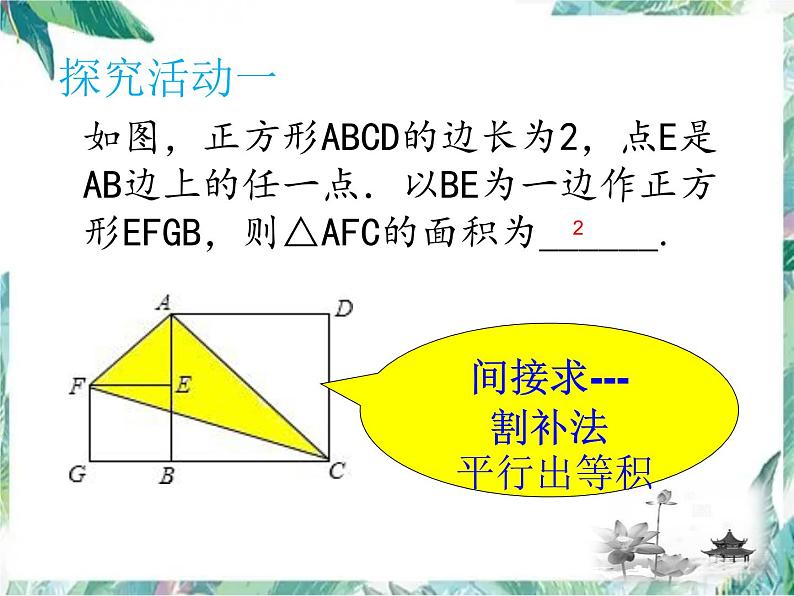
如图，正方形ABCD的边长为2，点E是AB边上的任一点．以BE为一边作正方形EFGB，则△AFC的面积为______.
要求：1、独立思考2分钟2、组内合作交流2分钟3、小组展示交流成果
间接求---割补法 平行出等积
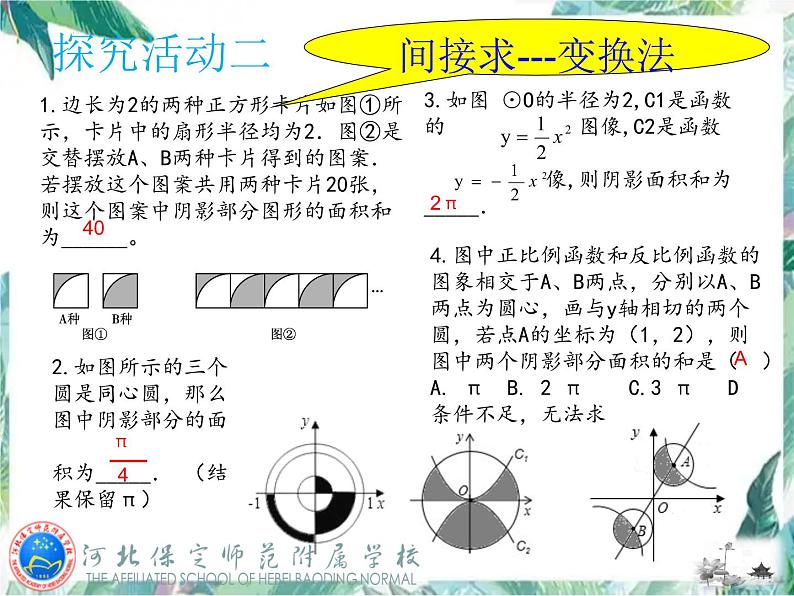
1.边长为2的两种正方形卡片如图①所示，卡片中的扇形半径均为2．图②是交替摆放A、B两种卡片得到的图案．若摆放这个图案共用两种卡片20张，则这个图案中阴影部分图形的面积和为______。
3.如图 ⊙O的半径为2,C1是函数 的 图像,C2是函数 的图像,则阴影面积和为_____．
2.如图所示的三个圆是同心圆，那么图中阴影部分的面积为_____． （结果保留π）
4.图中正比例函数和反比例函数的图象相交于A、B两点，分别以A、B两点为圆心，画与y轴相切的两个圆，若点A的坐标为（1，2），则图中两个阴影部分面积的和是（ ）A. π B. 2 π C.3 π D 条件不足，无法求
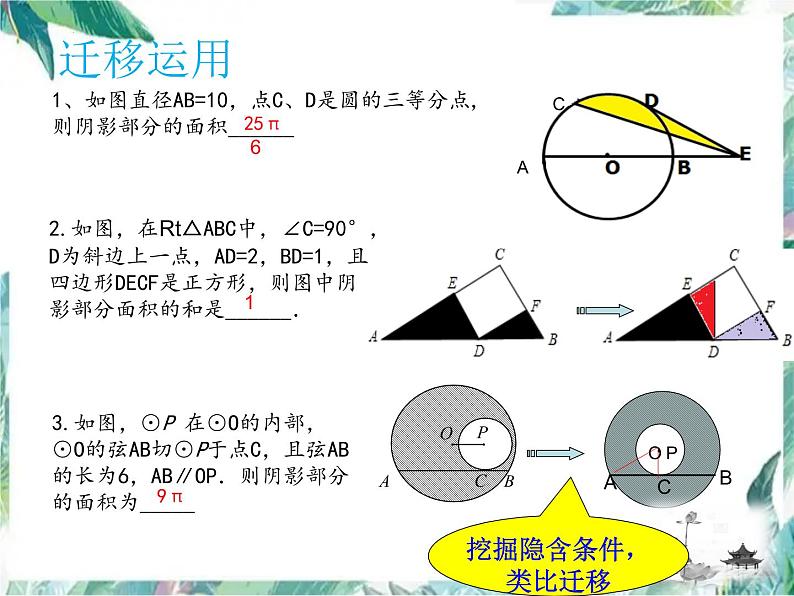
3.如图，⊙P 在⊙O的内部，⊙O的弦AB切⊙P于点C，且弦AB的长为6，AB∥OP．则阴影部分的面积为_____
2.如图，在Rt△ABC中，∠C=90°，D为斜边上一点，AD=2，BD=1，且四边形DECF是正方形，则图中阴影部分面积的和是______．
1、如图直径AB=10，点C、D是圆的三等分点, 则阴影部分的面积______
挖掘隐含条件，类比迁移
类型一 阴影部分周长的计算
类型二 阴影部分面积的计算
1.⊙O与直线L切于A点, 点P.点Q同时从A点出发，点P沿着直线L向右、点Q沿着圆周按逆时针以相同的速度运动，当点Q到达点A时，点P也停止运动.则S1、S2的大小关系是（ ） A.S1=S2 B.先S1S2 C.S1≤S2 D. S1≥S2
2.O是正方形ABCD的中心，OE ⊥ BC于点E,点P、点Q同时从点E出发，点P沿着射线BC向右、点Q沿着正方形按逆时针以相同的速度运动，当点Q到达点E时，点P也停止运动.则S1、S2的大小关系是（ ） A.S1=S2 B.先S1S2 C.S1≤S2 D. S1≥S2
这节课我们探究了什么问题？解决这类问题的策略与方法是什么？经历这个探究过程，你有何感受和体会？