还剩16页未读，继续阅读

下载需要20学贝 1学贝=0.1元

使用下载券免费下载

加入资料篮

立即下载

所属成套资源：2022学年全国部分地区高中数学第三次模拟测试卷（含答案解析）

成套系列资料，整套一键下载

浏览整套资料 (共10份)

2022年广西柳州市高考数学三模试卷（理科）（含答案解析）

展开

这是一份2022年广西柳州市高考数学三模试卷（理科）（含答案解析），共19页。

2022年广西柳州市高考数学三模试卷（理科）

设集合，，则

A. B. C. D.

已知i为虚数单位，则在复平面内对应的点位于

A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

不等式“”是“”成立的

A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件

已知随机变量，若函数为偶函数，则

A. 2 B. 1 C. 0 D.

某校组织全体学生参加了主题为“奋斗百年路，启航新征程”的知识竞赛，随机抽取了100名学生进行成绩统计，发现抽取的学生的成绩都在50分至100分之间，进行适当分组后每组的取值区间均为左闭右开区间，画出频率分布直方图如图，下列说法不正确的是

A. 在被抽取的学生中，成绩在区间内的学生有10人
B. 这100名学生成绩的众数为85
C. 估计全校学生成绩的平均分数为78
D. 这100名学生成绩的中位数为80

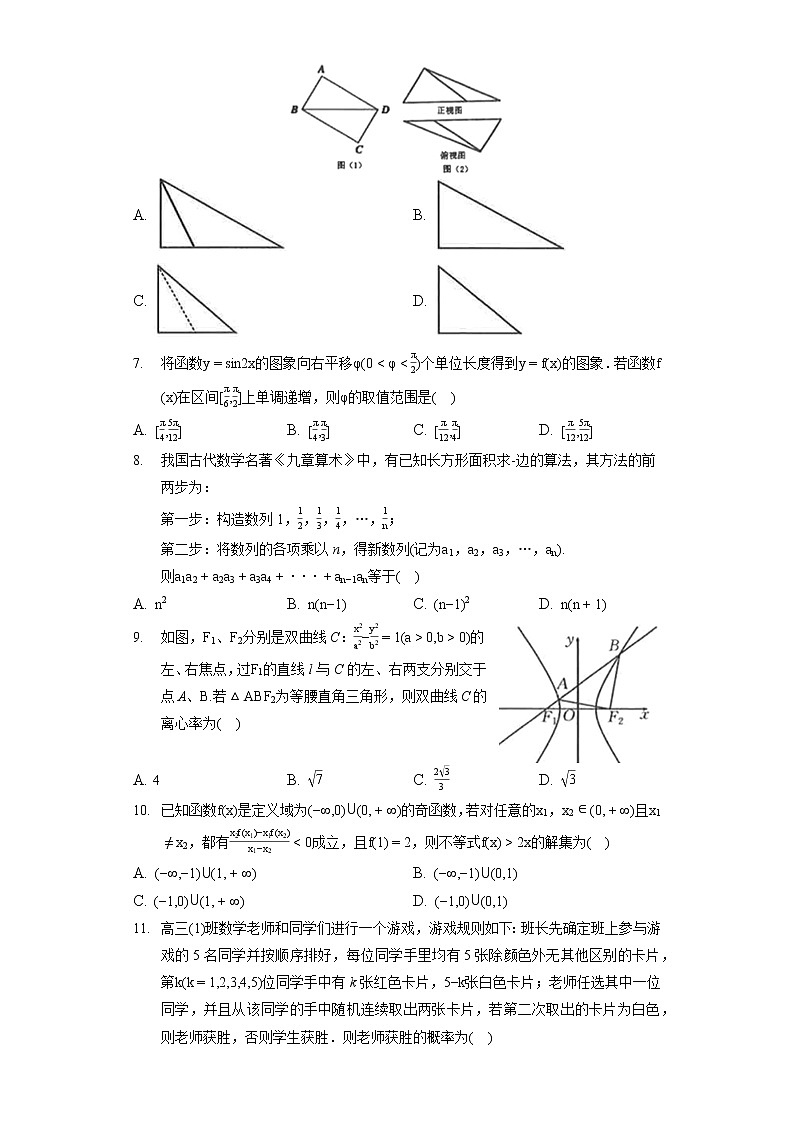
如图，沿对角线BD将矩形折叠，连接AC，所得三棱锥正视图和俯视图如图，则三棱锥的侧视图为

A. B.
C. D.

将函数的图象向右平移个单位长度得到的图象．若函数在区间上单调递增，则的取值范围是

A. B. C. D.

我国古代数学名著《九章算术》中，有已知长方形面积求-边的算法，其方法的前两步为：
第一步：构造数列1，，，，…，；
第二步：将数列的各项乘以n，得新数列记为，，，…，
则等于

A. B. C. D.

如图，、分别是双曲线C：的左、右焦点，过的直线l与C的左、右两支分别交于点A、若为等腰直角三角形，则双曲线C的离心率为

A. 4 B. C. D.

已知函数是定义域为的奇函数，若对任意的，且，都有成立，且，则不等式的解集为

A. B.
C. D.

高三班数学老师和同学们进行一个游戏，游戏规则如下：班长先确定班上参与游戏的5名同学并按顺序排好，每位同学手里均有5张除颜色外无其他区别的卡片，第位同学手中有k张红色卡片，张白色卡片；老师任选其中一位同学，并且从该同学的手中随机连续取出两张卡片，若第二次取出的卡片为白色，则老师获胜，否则学生获胜．则老师获胜的概率为

A. B. C. D.

若曲线在点处的切线方程为，则的最大值为

A. B. 1 C. D. e

已知平面向量，，若，则______.
已知抛物线C：的焦点为F，过F且垂直于x轴的直线l与C交于A、B两点，则以线段AB为直径的圆被y轴所截得的弦长为______.
已知数列的首项，其前n项和为，若，则______.
已知对棱相等的四面体被称为“等腰四面体”，它的四个面是全等的锐角三角形．在等腰四面体中，，，则该四面体的内切球表面积为______.
在中，a，b，c分别为角A，B，C的对边，已知
求角A的大小；
若b，a，c成等比数列，判断的形状．
某公司拟对某种材料进行应用改造，产品的成本由原料成本及非原料成本组成，每件产品的非原料成本元与生产该产品的数量千件有关，经统计得到如下数据：

x	1	2	3	4	5	6	7	8
y	112	61		35		28	25	24

对历史数据对比分析，考虑用函数模型①，②分别对两个变量的关系进行拟合，令模型①中上，模型②中，对数据作了初步处理，已计算得到如下数据：


	45

设u和y的样本相关系数为，x和w的样本相关系数为，已经计算得出，请从样本相关系数精确到的角度判断，哪个模型拟合效果更好？
根据的选择及表中数据，建立y关于x的非线性回归方程，并用其估计当每件产品的非原料成本为21元时，产量约为多少千件？
参考公式：对于一组数据，，…，其回归直线的斜率和截距的最小二乘估计分别为：，，相关系数

已知四棱锥中，，平面ABC，点M为AE三等分点靠近A点，，，
求证：平面ABC；
求二面角的余弦值．

若
当，时，讨论函数的单调性；
若，且有两个极值点，，证明：
已知点，点，点M与y轴的距离记为d，且点M满足：，记点M的轨迹为曲线
求曲线W的方程；
设点P为x轴上除原点O外的一点，过点P作直线，，交曲线W于点C，D，交曲线W于点E，F，G，H分别为CD，EF的中点，过点P作x轴的垂线交GH于点N，设CD，EF，ON的斜率分别为，，的，求证：为定值．
如图，在极坐标系中，已知点，曲线是以极点O为圆心，以OM为半径的半圆，曲线是过极点且与曲线相切于点的圆．
求曲线、的极坐标方程；
直线与曲线、分别相交于点A，异于极点，求面积的最大值．

已知函数
若，求不等式的解集；
若，使得能成立，求实数m的取值范围．

答案和解析

1.【答案】C

【解析】解：，，
则
故选：
先分别求出集合U，M，然后结合集合补集的定义即可求解．
本题主要考查了集合补集的定义，属于基础题．

2.【答案】C

【解析】解：，
在复平面内对应的点位于第三象限．
故选：
根据已知条件，结合复数的乘除法原则和复数的几何意义，即可求解．
本题考查了复数的几何意义，以及复数代数形式的乘除法运算，需要学生熟练掌握公式，属于基础题．

3.【答案】A

【解析】解：，，，
，，，
不等式“”是“”成立的充分不必要条件．
故选：
，，由此能求出结果．
本题考查充分条件、必要条件的判断，考查指数函数、对数函数的性质等基础知识，考查运算求解能力，是基础题．

4.【答案】B

【解析】解：函数为偶函数，
，即，

故选：
根据已知条件，结合偶函数和正态分布的性质，即可求解．
本题主要考查正态分布的对称性，以及偶函数的性质，属于基础题．

5.【答案】D

【解析】解：选项A，成绩在区间的频率为，则人数为，故A正确；
选项B，由频率分布直方图可知，学生成绩的众数为85，故B正确；
选项C，全校学生成绩的平均分数为，故C正确；
选项D，成绩在区间的频率为成绩在区间的频率为，
成绩在区间的频率为，成绩在区间的频率为，
由，
所以这100名学生成绩的中位数在之间，设为x，
则，解得，故D不正确，
故选：
根据频率分布直方图可求出成绩在区间的频率，从而判断选项A，根据频率分布直方图可得众数，由平均数的计算公式可得平均分数，从而判断选项B，C，成绩的中位数在之间，设为x，由面积可得答案．
本题主要考查频率分布直方图的应用，考查计算能力，属于基础题．

6.【答案】D

【解析】解：由题设，作出三棱锥的直观图，如图，

结合图形得面面BCD，
三棱锥的侧视图为：

故选：
由题图还原三棱锥直观图，注意相关平面的位置关系，即可判断侧视图．
本题考查三棱锥的侧视图的判断，考查三棱锥的直观图、三视图等基础知识，考查空间想象能力，是基础题．

7.【答案】A

【解析】解：将函数的图象向右平移个单位长度得到的图象，
若函数在区间上单调递增，，
则，，，
求得，，
令，可得，
故选：
由题意，利用函数的图象变换规律，正弦函数的单调性，求得的范围．
本题主要考查函数的图象变换规律，正弦函数的单调性，属于中档题．

8.【答案】B

【解析】解：由题意可得：，
…
，
故选：
由题意可得：，进而得出结论．
本题考查了裂项求和方法、转化方法，考查了推理能力与计算能力，属于基础题．

9.【答案】D

【解析】解：由双曲线的定义可得，①
为等腰直角三角形，，
，
，②
联立①②解得，，
，，
在中，有，
整理得：，即
故选：
由已知结合双曲线的定义求解、，在中，由余弦定理列式求解双曲线的离心率．
本题考查双曲线的几何性质，考查双曲线定义的应用，考查运算求解能力，是中档题．

10.【答案】B

【解析】解：对任意的，且，都有成立，
即，可得在上单调递减，
而函数是定义域为的奇函数，
所以为偶函数，在上单调递增，
所以不等式等价为或，
所以或，
所以不等式的解集为
故选：
由单调性的定义可得在上单调递减，判断为偶函数，在上单调递增，分别讨论，，可得原不等式的等价形式，解不等式可得不等式的解集．
本题考查函数的奇偶性和单调性的判断和运用，考查转化思想和运算能力，属于中档题．

11.【答案】B

【解析】解：当时，连续取出两张卡片的和种数为种，
第二张为白色的种数为种，概率为；
当时，连续取出两张卡片的种数为种，
第二张为白色的种数为种，概率为；
当时，连续取出两张卡片的种数为种，
第二张为白色的种数为种，概率为；
当时，连续取出两张卡片的种数为种，
第二张为白色的种数为种，概率为；
当时，连续取出两张卡片的种数为种，
第二张为白色的种数为0种，概率为
又老师选每位学生的概率为，
老师获胜的概率为：
故选：
分情况讨论k取不同值时老师获胜的概率，由此能求出结果．
本题考查概率的求法，考查互斥事件概率加法公式等基础知识，考查运算求解能力，是基础题．

12.【答案】A

【解析】解：的导数为，
可得在处的切线的斜率为，
，则，
所以，
设，导数为，
当时，，递减；当时，，递增，
可得在处取得极大值，且为最大值
所以的最大值为
故选：
求得的导数，可得切线的斜率和切点，求得k，b，构造新函数，求得导数和单调性、极值和最值．
本题考查导数的运用：求切线的方程和单调性、极值和最值，考查方程思想和运算能力，属于中档题．

13.【答案】

【解析】解：根据题意，向量，，
若，则有，即，
则，故，
故，
故答案为：
根据题意，由向量平行的坐标表示方法可得k的值，即可得的坐标，进而计算可得答案．
本题考查向量模的计算，涉及向量平行的坐标计算，属于基础题．

14.【答案】

【解析】解：由抛物线C的方程：，可得它的的焦点，
令，代入抛物线的方程可得，解得，
所以由题意以AB为直径的圆的方程为：，
令，则，可得，
所以弦长为，
故答案为：
由抛物线的方程可得焦点F的坐标，由题意求出过焦点F且垂直于x轴的直线，与抛物线的方程联立，求出A，B的纵坐标，可得以AB为直径的圆的方程，令，可得圆与y轴的交点的纵坐标，求出弦长的值．
本题考查抛物线的性质的应用即圆的方程的求法，属于中档题．

15.【答案】16

【解析】解：数列的首项，其前n项和为，，
可得，所以，
，可得，
，解得，
，解得
故答案为：
利用数列的递推关系式逐步求解即可．
本题考查数列的递推关系式的应用，数列项的求法，是基础题．

16.【答案】

【解析】解：如图示，将等腰四面体补成一个长方体，
设，，，
则，解得，
故四面体的体积为，
设该四面体的内切球的半径为r，
则，
而，
故，
则该四面体的内切球表面积为，
故答案为：
首先将四面体补成一个长方体，求得长方体棱长，从而求得四面体的体积，再根据等体积的方法，运算割补法，求得内切球的半径，求得答案．
本题考查了四面体的内切球问题，属于中档题．

17.【答案】解：因为，由诱导公式得，
由正弦定理得，
，
，
，
，

，a，c成等比数列，
，
又因为，
，
，
，
又，为等边三角形．

【解析】由诱导公式，正弦定理，同角三角函数基本关系式化简已知等式可得，结合范围，可求A的值．
由题意利用等比数列的性质可求，利用余弦定理，平方差公式可求，结合，即可判断三角形的形状．
本题主要考查了诱导公式，正弦定理，同角三角函数基本关系式，等比数列的性质，余弦定理在解三角形中的应用，考查了计算能力和转化思想，属于中档题．

18.【答案】解：因为，令，
则，
可转化为，y与u的相关系数为：，
因为，
所以用反比例函数模型拟合效果更好．
，
则，
所以y关于x的回归方程为，
当时，，
解得，
所以当每件产品的非原料成本为21元时，预计产量约为10千件．

【解析】根据已知条件，结合相关系数的公式，求出，再通过比较相关系数，即可求解．
根据已知条件，结合最小二乘法公式，即可求解．
本题主要考查了线性回归方程的求解，需要学生熟练掌握最小二乘法公式，属于中档题．

19.【答案】证明：取AC三等分点N，

，，
，
且，又，，
且，
四边形BNMF为平行四边形，
，
又平面ABC，平面ABC，
平面
解：法一：平面BFM即平面BFMN，
且，平面ABC，
平面ABC，
为所求二面角的平面角，，，
由余弦定理得：，
，
所求二面角的余弦值为
法二：以AC的中点O为坐标原点，以OB为x轴，OA为y轴建系如图所示：

，，，，，
，，，
设平面ABF的法向量为，平面BFMN的法向量为，
，
，
可得，不妨取，
，
，
可得，不妨取，
所以，
二面角的余弦值为

【解析】取AC三等分点N，证明四边形BNMF为平行四边形，推出，即可证明平面
法一：说明为所求二面角的平面角，利用余弦定理求解二面角的余弦值即可．
法二：以AC的中点O为坐标原点，以OB为x轴OA为y轴建系，求出平面ABF的法向量，平面BFMN的法向量，利用空间向量的数量积求解二面角的余弦值即可．
本题考查直线与平面平行的判断定理的应用，二面角的平面角的求法，考查空间想象能力，转化思想以及计算能力，是中档题．

20.【答案】解：因为，
当，时，，
令，解得或2，
①当时，当或时，；当时，，
所以函数在，上单调递增，在上单调递减，
②当时，，故函数在上单调递增，
③当时，当或时，；当时，，
所以函数在，上单调递增，在上单调递减．
证明：当时，，
因为函数有两个极值点，所以方程有两个正根，，
则，，，解得，
由题意得
，
令，，，则，
所以在上单调递减，
所以，即

【解析】根据题意可得，当，时，，令，解得或2，再分，和三种情况，讨论的单调性．
当时，，若函数有两个极值点，则方程有两个正根，，，得，化简得，令，，求出最小值，即可得出答案．
本题考查导数的综合应用，考查了分类讨论思想和转化思想，属于中档题．

21.【答案】解：设，由题意得，，，
由，
，

，
M的轨迹方程为
法一：
显然GH斜率存在，设，设GH的方程为：，
由题意知CD的方程为：，
联立方程，
解得：，
可得：，
设，，C，D都在曲线W上，则有①，②
①-②得：，
则有：，
又G为CD中点，则有；，
可得：，
同理可得：，
故，为关于k的方程的两实根，
由韦达定理得：，
将代入直线GH中得：，
可得：，
故有：，
则，
故为定值
法二：
由题意知直线CD，EF，ON的斜率都存在，分别为，，，
设，，
则直线CD的方程为：，
直线EF的方程为：，
分别与自线W相交，联立方程，
解得：，
可得：，
同理可得：，
由题意知G、H、N三点共线，
，即，
化简整理得：，
即：，
，
，
故为定值

【解析】设，由题意得，利用向量的数量积推出结果即可．
法一：设，设GH的方程为：，CD的方程为：，求出G的坐标，设，，C，D都在曲线W上，说明，为关于k的方程的两实根，韦达定理得：，求解N的坐标，得到，然后求解为定值
法二：直线CD，EF，ON的斜率都存在，分别为，，，设，，直线CD的方程为：，直线EF的方程为：，求出，，说明，转化推出为定值．
本题考查椭圆方程的求法，直线与椭圆的位置关系的综合应用，考查分析问题解决问题的能力，是中档题．

22.【答案】解：由题意可知，曲线是以极点O为圆心，以2为半径的半圆，
结合图形可知，曲线的极坐标方程为；
设为曲线上的任意一点，可得，
因此，曲线极坐标方程为
解：因为直线与曲线，分别相交于点A，异于极点，
设，，由题意得，，
所以，
因为点M到直线AB的距离为，
所以
当且仅当时，等号成立，故面积的最大值为