专题01 【精品】手拉手模型-2022年中考数学几何模型解题策略研究（课件+讲义）

这是一份专题01 【精品】手拉手模型-2022年中考数学几何模型解题策略研究（课件+讲义），文件包含专题01手拉手模型pptx、专题01手拉手模型解析版doc、专题01手拉手模型原卷版doc等3份课件配套教学资源，其中PPT共40页， 欢迎下载使用。
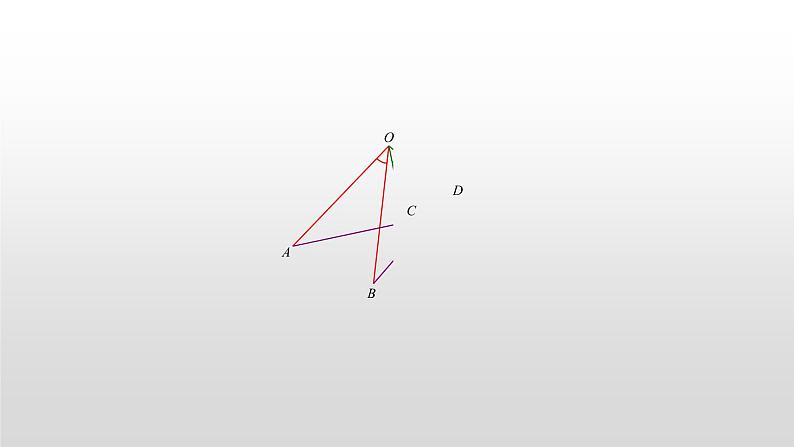
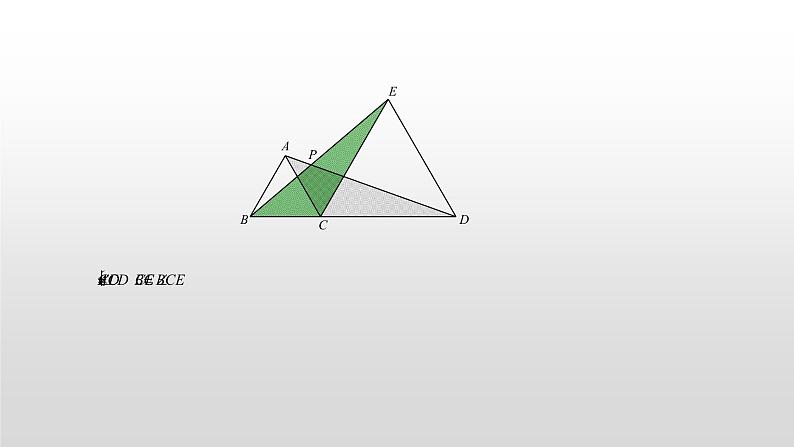
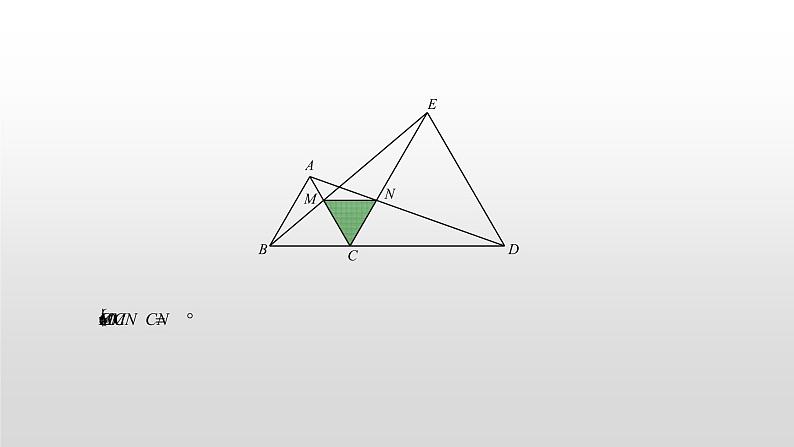
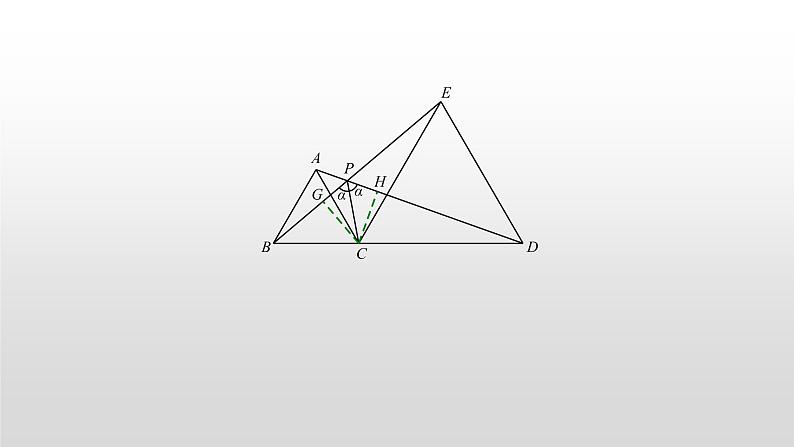
专题01 手拉手模型一、方法突破问题一：构成手拉手的必要条件．当对一个几何图形记忆并不深刻的时候，可以尝试用文字取总结要点，比如手拉手：四线共点，两两相等，夹角相等． 条件：如图，OA=OB，OC=OD（四线共点，两两相等），∠AOB=∠COD（夹角相等）结论：△OAC≌△OBD（SAS）证明无需赘述，关于条件中的OA=OB，OC=OD，有时候会直接以特殊几何图形的形式给出，比如我们都很熟悉的等边三角形和正方形． 1．等边三角形手拉手（1）如图，B、C、D三点共线，△ABC和△CDE是等边三角形，连接AD、BE，交于点P： 结论一：△ACD≌△BCE证明： → △ACD≌△BCE（SAS）（2）记AC、BE交点为M，AD、CE交点为N：结论二：△ACN≌△BCM；△MCE≌△NCD证明： → △ACN≌△BCM（SAS）； → △MCE≌△NCD（ASA）（3）连接MN：结论三：△MNC是等边三角形．证明：→△MCN是等边三角形．（4）记AD、BE交点为P，连接PC：结论四：PC平分∠BPD证明：△BCE≌△ACD → CG=CH → PC平分∠BPD．
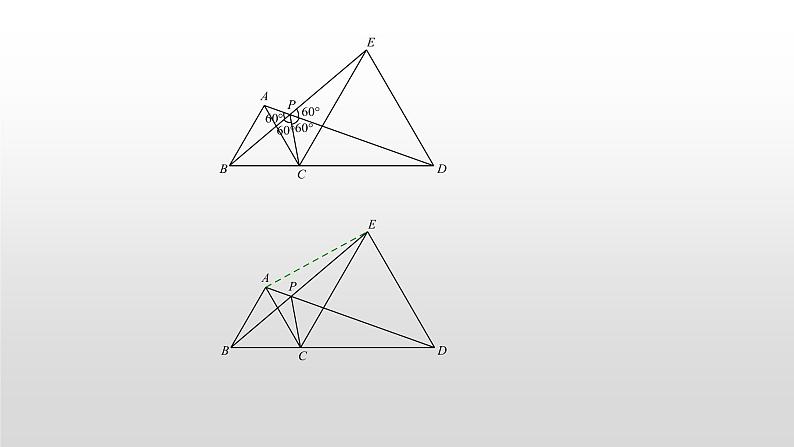
（5）结论五：∠APB=∠BPC=∠CPD=∠DPE=60°．（6）连接AE：结论六：P点是△ACE的费马点（PA+PC+PE值最小） 2．正方形手拉手如图，四边形ABCD和四边形CEFG均为正方形，连接BE、DG：结论一：△BCE≌△DCG证明： → △BCE≌△DCG（SAS）结论二：BE=DG，BE⊥DG证明：△BCE≌△DCG → BE=DG；∠CBE＝∠CDG → ∠DHB=∠BCD=90°（旋转角都相等） 【重点概述】手拉手模型是一种基本的旋转型全等，与其说看图找模型，不如是“找条件、定模型”． 问题二：条件与结论如何设计？设计一：我们可以给出手拉手模型条件，得到一组全等来解决问题，就像问题一中所得出的结论那样；设计二：如果题目已知△ABC≌△ADE外，则还可得△ABD和△ACE均为等腰三角形，且有△ABD∽△ACE，．问题三：如何构造手拉手？如何构造手拉手？换句话说，如何构造旋转？当我们在思考这个问题的时候，不妨先问一句，旋转能带来什么？图形位置的改变，这一点就够了，因为，若有数量关系，则先有位置关系． 二、典例精析例一：如图，等边三角形的边长为4，点是的中心，，绕点旋转，分别交线段、于、两点，连接，给出下列四个结论：①；②；③四边形的面积始终等于；④周长的最小值为6．上述结论中正确的个数是　　A．1 B．2 C．3 D．4例二：如图，点在等边的内部，且，，，将线段绕点顺时针旋转得到，连接，则的值为　 　．例三：如图，是等边三角形内一点，将线段绕点顺时针旋转得到线段，连接．若，，，则四边形的面积为　 　．例四：如图，等边三角形内有一点，分別连结、、，若，，．则　　． 例五：如图，为等边三角形内的一点，且到三个顶点，，的距离分别为3，4，5，则的面积为　　A． B． C． D．例六：在Rt△ABC中，AB=AC，点P是三角形内一点且∠APB=135°，，AC的最大值为_________．三、中考真题演练1．（2021•日照）问题背景：如图1，在矩形中，，，点是边的中点，过点作交于点．实验探究：（1）在一次数学活动中，小王同学将图1中的绕点按逆时针方向旋转，如图2所示，得到结论：①　　；②直线与所夹锐角的度数为 　　．（2）小王同学继续将绕点按逆时针方向旋转，旋转至如图3所示位置．请问探究（1）中的结论是否仍然成立？并说明理由．拓展延伸：在以上探究中，当旋转至、、三点共线时，则的面积为 　　．2．（2021•贵港）已知在中，为边的中点，连接，将绕点顺时针方向旋转（旋转角为钝角），得到，连接，．（1）如图1，当且时，则与满足的数量关系是 　　；（2）如图2，当且时，（1）中的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由．（3）如图3，延长到点，使，连接，当，时，求的长．3．（2021•黑龙江）在等腰中，，是直角三角形，，，连接、，点是的中点，连接．（1）当，点在边上时，如图①所示，求证：；（2）当，把绕点逆时针旋转，顶点落在边上时，如图②所示，当，点在边上时，如图③所示，猜想图②、图③中线段和又有怎样的数量关系？请直接写出你的猜想，不需证明．4．（2021•通辽）已知和都是等腰直角三角形，．（1）如图1，连接，，求证：；（2）将绕点顺时针旋转．①如图2，当点恰好在边上时，求证：；②当点，，在同一条直线上时，若，，请直接写出线段的长．5．（2021•十堰）已知等边三角形，过点作的垂线，点为上一动点（不与点重合），连接，把线段绕点逆时针方向旋转得到，连．（1）如图1，直接写出线段与的数量关系；（2）如图2，当点、在同侧且时，求证：直线垂直平分线段；（3）如图3，若等边三角形的边长为4，点、分别位于直线异侧，且的面积等于，求线段的长度．6．（2020•沈阳）在中，，，点为线段延长线上一动点，连接，将线段绕点逆时针旋转，旋转角为，得到线段，连接，．（1）如图1，当时，①求证：；②求的度数；（2）如图2，当时，请直接写出和的数量关系．（3）当时，若，，请直接写出点到的距离为　或　．