专题04【精品】 旋转之从全等到相似-2022年中考数学几何模型解题策略研究（课件+讲义）

这是一份专题04【精品】 旋转之从全等到相似-2022年中考数学几何模型解题策略研究（课件+讲义），文件包含专题04旋转之从全等到相似pptx、专题04旋转之从全等到相似解析版doc、专题04旋转之从全等到相似原卷版doc等3份课件配套教学资源，其中PPT共16页， 欢迎下载使用。
专题04 旋转之从全等到相似一、方法突破在手拉手模型中，我们可以看成是两个相似的等腰三角形作共点旋转，由等腰条件可得一组全等三角形．若△ABC与△ADE非等腰，则可得到旋转型相似，取直角三角形为例．如图，Rt△ABC∽Rt△ADE，连接BD、CE，可得：△ADB∽△AEC，（利用两边对应成比例且夹角相等）且旋转的性质，旋转角都相等依然成立，如下右图，∠BAD=∠EAC=∠EFB．  
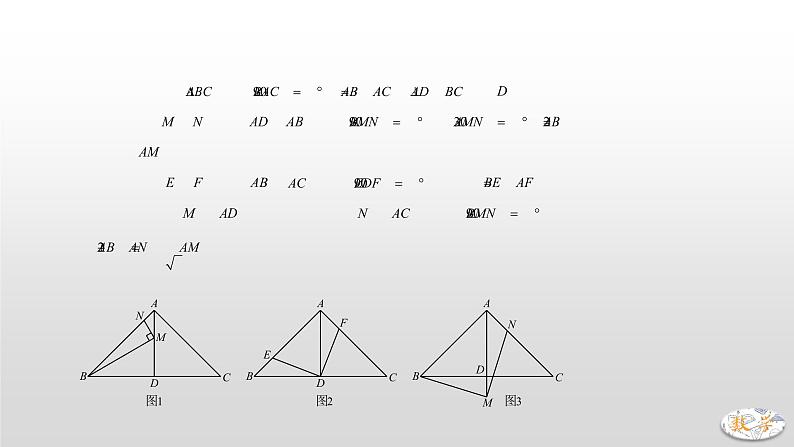
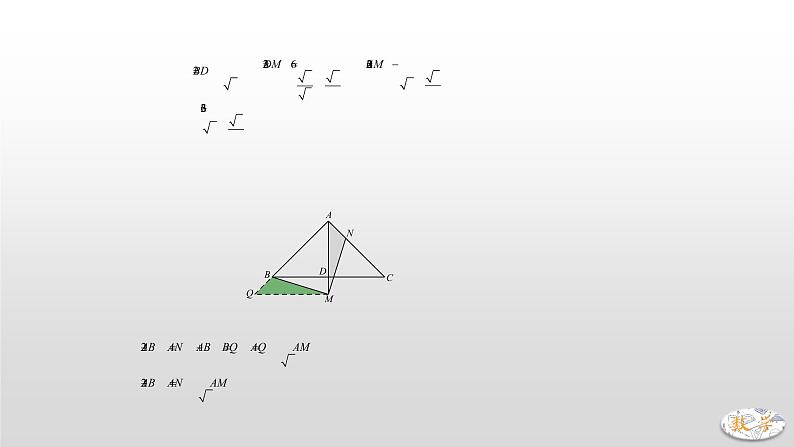
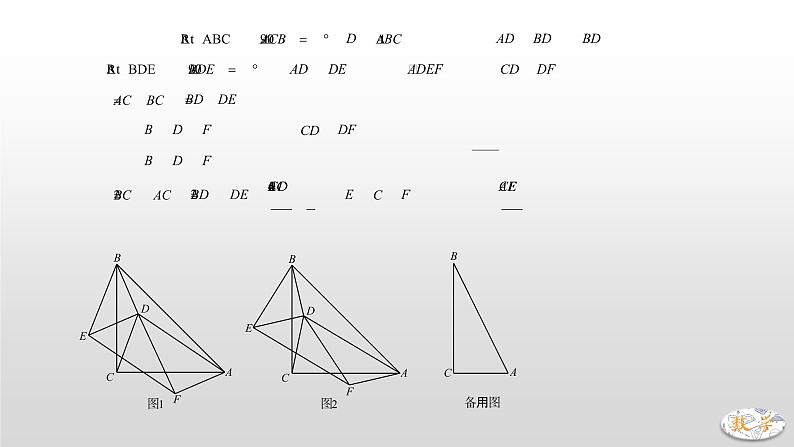
二、典例精析【旋转全等】1.（2019·枣庄）在中，，，于点．（1）如图1，点，分别在，上，且，当，时，求线段的长；（2）如图2，点，分别在，上，且，求证：；（3）如图3，点在的延长线上，点在上，且，求证：．【分析】（1）∵∠AMN=30°，∴∠BMD=60°，∵AB=2，∴，∴，∴．故AM的值为．（2）易证△BDE≌△ADF，∴BE=AF．（3）如图，作MQ⊥MA交AB延长线于点Q，易证△MAN≌△MQB，∴AN=BQ，∴，∴．
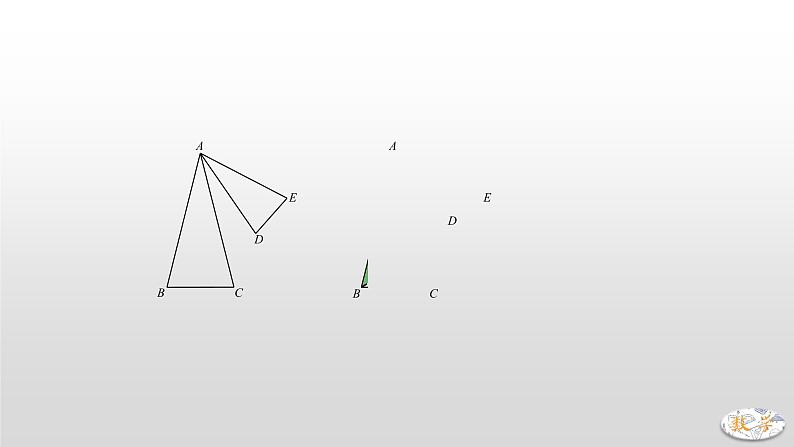
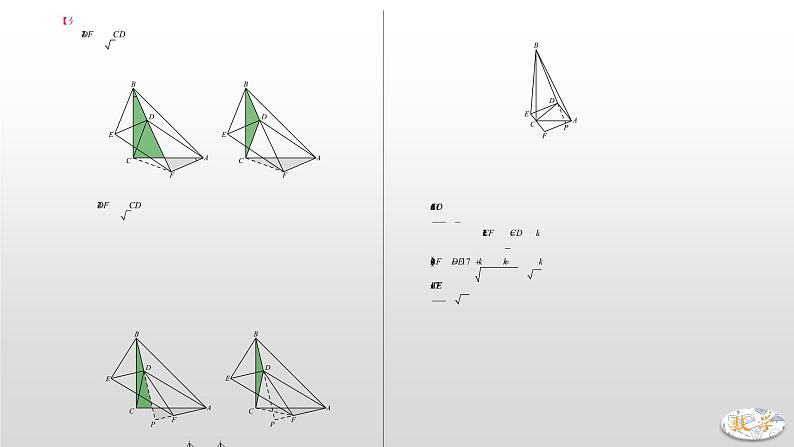
【从全等到相似】2.（2019·鞍山）在中，，是内一点，连接，．在左侧作，使，以和为邻边作，连接，．（1）若，．①如图1，当，，三点共线时，与之间的数量关系为　　．②如图2，当，，三点不共线时，①中的结论是否仍然成立？请说明理由．（2）若，，，且，，三点共线，求的值． 【分析】（1）．由“8字”模型易证：∠CBD=∠CAF，连接CF，易证△CDB≌△CFA，∴CD=CF，且∠DCF=∠BCA=90°，∴．（2）成立，类似还是证明△CDB≌△CFA，而其中关键性条件∠CBD=∠CAF与B、D、F共线与否比并无关系．BD与DE是垂直关系，又AF∥DE，∴BD⊥AF．如下图，延长BD与AF交于点P，则∠P=90°，由“8字”模型可证：∠CBD=∠CAF．易证△CDB≌△CFA，∴．（3）参考（2），延长BD与AF交于点P，则BD⊥AF，由“8字”模型可得：∠CBD=∠CAF，又BC=2AC，BD=2DE=2AF，∴△CDB∽△CFA，∴CD=2CF．∵，不妨设CD=4k，则AC=5k，∴AD=EF=3k，，∴CE=k，∴，∴．
【旋转相似】3.（2019·襄阳）如图，两个大小不同的三角板放在同一平面内，直角顶点重合于点，点在上，，与交于点，连接，若，，则　　．【分析】易证△CBD∽△CAE，且，∴，∠CAE=∠CBD，∴∠BAE=∠BAC+∠CAE=∠BAC+∠CBD=90°，∴，∴，，又∠CAF=∠CBD=∠CDE=60°，∴△CFD∽△EFA，∴，故的值为．
【旋转相似】4.（2019·东营）如图1，在中，，，，点、分别是边、的中点，连接．将绕点逆时针方向旋转，记旋转角为．（1）问题发现①当时，　　；②当时，　　．（2）拓展探究试判断：当时，的大小有无变化？请仅就图2的情形给出证明．（3）问题解决绕点逆时针旋转至、、三点在同一条直线上时，求线段的长．
【分析】（1），．（2）不变，易证△CDB∽△CEA，∴．（3）当点E在线段AB上时，如下图所示：易证△CDB∽△CEA，，∵，BC=2，∴BE=1,，∴AE=3，∴．当点E在AB延长线上时，易证四边形BCDE是矩形，∴BD=CE=．综上所述，BD的长为或． 
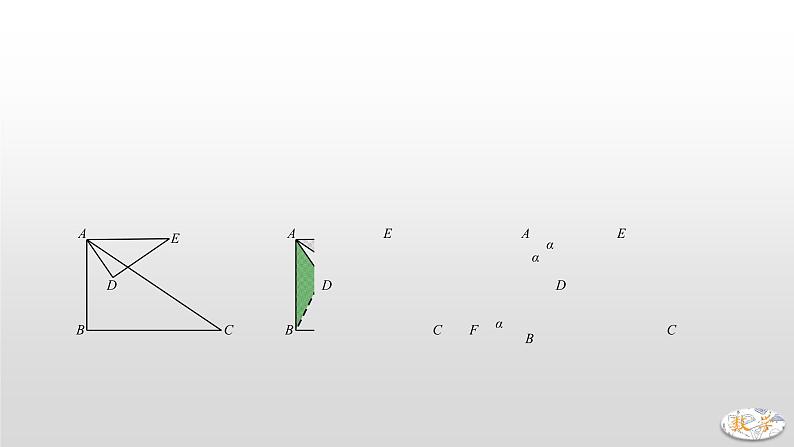
三、中考真题演练【旋转相似】1.（2019·宿迁）如图①，在钝角中，，，点为边中点，点为边中点，将绕点逆时针方向旋转度．（1）如图②，当时，连接、．求证：；（2）如图③，直线、交于点．在旋转过程中，的大小是否发生变化？如变化，请说明理由；如不变，请求出这个角的度数；（3）将从图①位置绕点逆时针方向旋转，求点的运动路程．【分析】（1）∵D、E分别是BA、BC中点，∴，，将△BDE旋转可得∠DBA=∠EBC=，∴△BDA∽△BEC．（2）不变．由（1）得△BDA∽△BEC，∴∠BAD=∠BCE，由“8字”模型可得：∠G=∠ABC=30°．（旋转任意均有△BED∽△BCA，且旋转角为30°，故CE与AD夹角始终为30°）（3）∠G所对的边AC为定边，定边对定角，故G点轨迹是个圆弧．以AC为边构造等边△AOC，点O即为圆心，又AC=4，故圆O半径为4．通过起点和终点来确定轨迹，如下图：G点从B点出发，当BD⊥BC时，弧BG最长，当旋转180°时，G点返回B点，故点G的轨迹是弧BG长的2倍．易证弧BG所对圆心角为60°，∴，∴G点轨迹长为． 【旋转相似】2.（2019·河南）在中，，．点是平面内不与点，重合的任意一点．连接，将线段绕点逆时针旋转得到线段，连接，，．（1）观察猜想如图1，当时，的值是　　，直线与直线相交所成的较小角的度数是　　．（2）类比探究如图2，当时，请写出的值及直线与直线相交所成的较小角的度数，并就图2的情形说明理由．（3）解决问题当时，若点，分别是，的中点，点在直线上，请直接写出点，，在同一直线上时的值．
【分析】（1）易证△APC≌△ADB，∴BD=CP，∴．根据“旋转角都相等”，可得直线BD与直线CP相交所成的较小角的度数是60°，可用“8字”模型证明：如下图，记BD与CP交于点Q，可得∠Q=∠CAB=60°．（2）易证△ADB∽△APC，∴．BD与CP所成的较小角是45°，如图所示，依然可用“8字”模型证明．（3）如下图，P、D、C共线，△APC是直角三角形，求的值，但AD与CP并无位置关系，故可转化比例，考虑到，∴可转化为求的值．情况一：过点P作MN⊥AB交BA延长线于点N，过点C作CM⊥MN交MN于点M．不妨设AN=x，PN=y，易证△PNA∽△CMP，，代入得：，化简得：，解得：，考虑到点P是MN中点，易证△ANP∽△APC，∴，∴．情况二：如下图所示，同上可求，，．综上所述，的值为或．
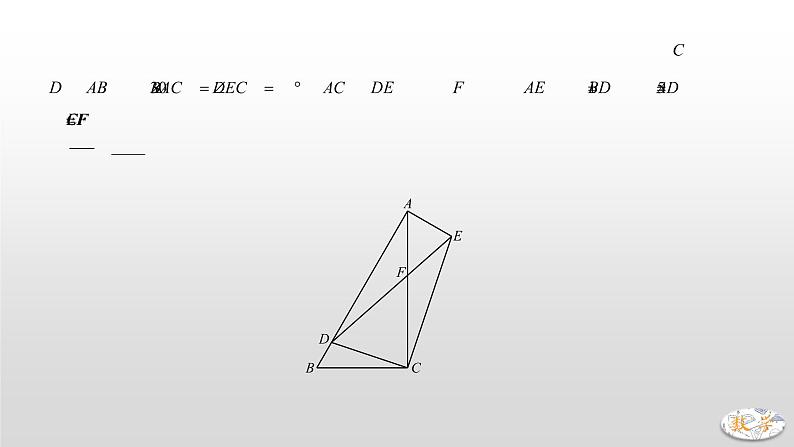
3.（2018·济南）在中，，，以为边在的另一侧作，点为射线上任意一点，在射线上截取，连接、、．（1）如图1，当点落在线段的延长线上时，直接写出的度数；（2）如图2，当点落在线段（不含边界）上时，与交于点，请问（1）中的结论是否仍成立？如果成立，请给出证明；如果不成立，请说明理由；（3）在（2）的条件下，若，求的最大值．【分析】（1）易证△ABD≌△ACE，∴∠BAD=∠CAE，AD=AE，∴∠BAD-∠CAD=∠CAE-∠CAD，即∠BAC=∠DAE，∴△ABC∽△ADE，∴∠ADE=∠ABC=30°．（2）成立．易证△ABD≌△ACE，易证△ABC∽△ADE，∴∠ADE=∠ABC=30°．（3）求CF最大值，等价于求AF最小值．∵∠ADF=∠ACD，∴△AFD∽△ADC，∴，即，∵AC=AB=6，∴，显然当AD⊥BC时，AD取到最小值3，此时，∴．故CF的最大值为．