专题11 【精品】将军饮马模型（二）-2022年中考数学几何模型解题策略研究（课件+讲义）

这是一份专题11 【精品】将军饮马模型（二）-2022年中考数学几何模型解题策略研究（课件+讲义），文件包含专题11将军饮马模型二pptx、专题11将军饮马模型二解析版doc、专题11将军饮马模型二原卷版doc等3份课件配套教学资源，其中PPT共24页， 欢迎下载使用。
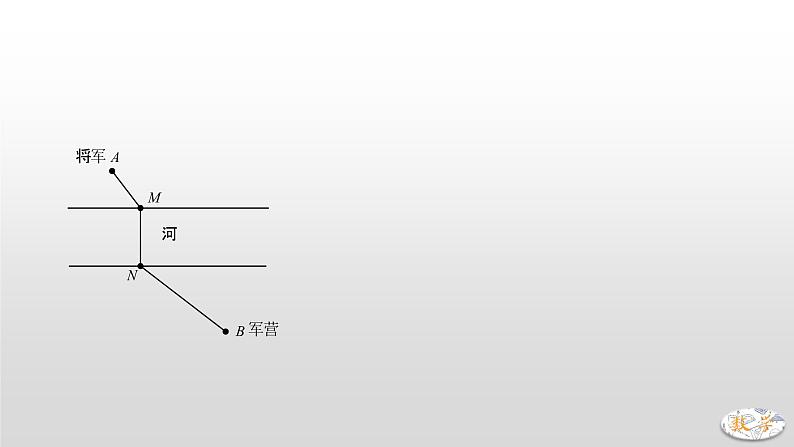
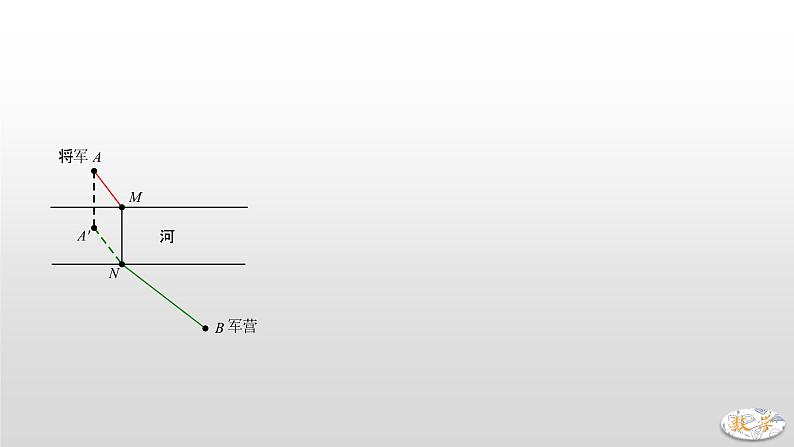
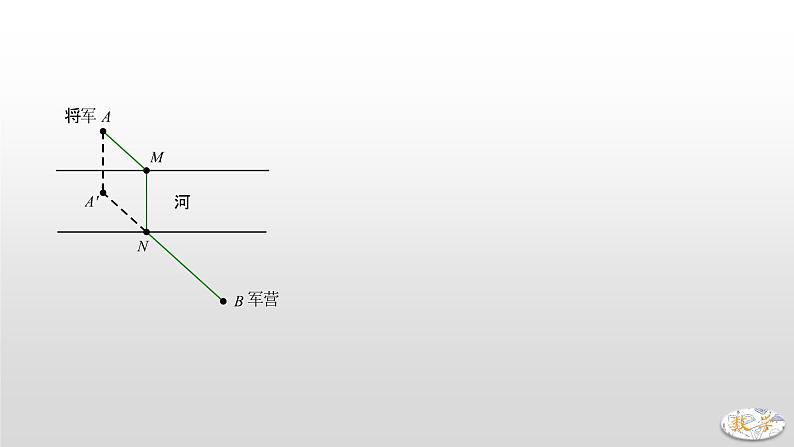
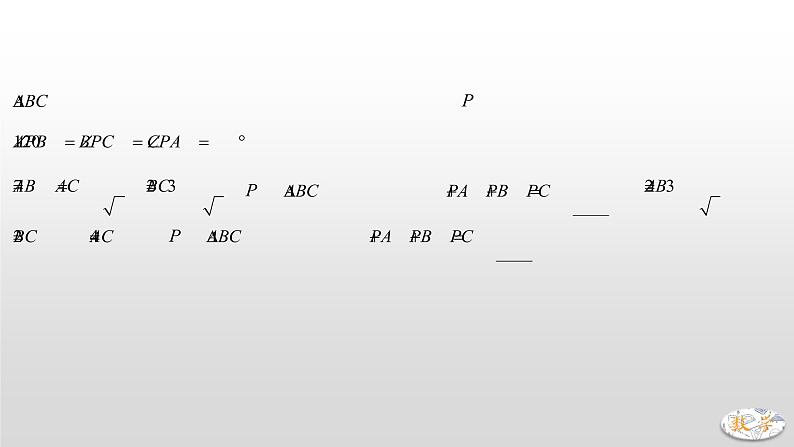
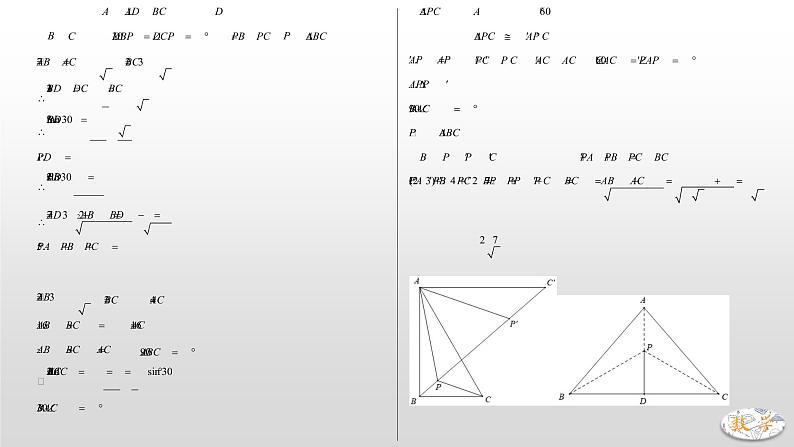
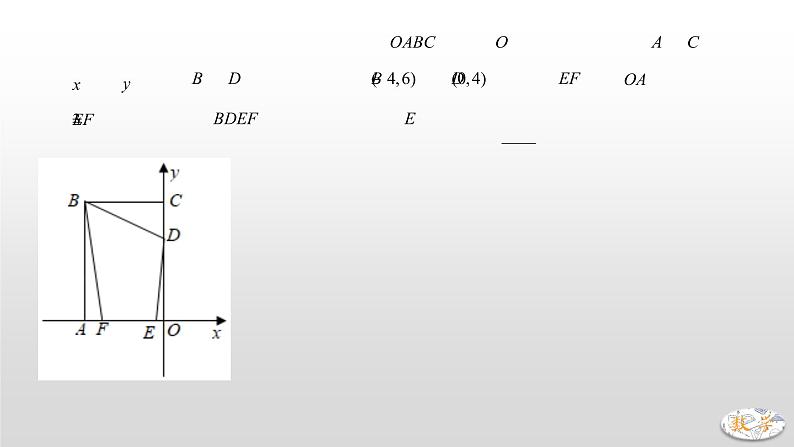
专题11 将军饮马模型（二）【将军过桥】已知将军在图中点A处，现要过河去往B点的军营，桥必须垂直于河岸建造，问：桥建在何处能使路程最短？考虑MN长度恒定，只要求AM+NB最小值即可．问题在于AM、NB彼此分离，所以首先通过平移，使AM与NB连在一起，将AM向下平移使得M、N重合，此时A点落在A’位置．问题化为求A’N+NB最小值，显然，当共线时，值最小，并得出桥应建的位置．中考真题演练1．（2021•丹东）已知：到三角形3个顶点距离之和最小的点称为该三角形的费马点．如果是锐角（或直角）三角形，则其费马点是三角形内一点，且满足．（例如：等边三角形的费马点是其三条高的交点）．若，，为的费马点，则　　；若，，，为的费马点，则　　．2．（2021•聊城）如图，在直角坐标系中，矩形的顶点在坐标原点，顶点，分别在轴，轴上，，两点坐标分别为，，线段在边上移动，保持，当四边形的周长最小时，点的坐标为 　　．3．（2020•贵港）如图，动点在边长为2的正方形内，且，是边上的一个动点，是边的中点，则线段的最小值为　　A． B． C． D．4．（2020•恩施州）如图，正方形的边长为4，点在上且，为对角线上一动点，则周长的最小值为　　A．5 B．6 C．7 D．85．（2020•西宁）如图，等腰的底边，面积为120，点在边上，且，直线是腰的垂直平分线，若点在上运动，则周长的最小值为　　．6．（2020•聊城）如图，在直角坐标系中，点，是第一象限角平分线上的两点，点的纵坐标为1，且，在轴上取一点，连接，，，，使得四边形的周长最小，这个最小周长的值为　　．7．（2019•聊城）如图，在中，，，点在边上，且，点为的中点，点为边上的动点，当点在上移动时，使四边形周长最小的点的坐标为　　A． B．， C．， D．8．（2018•滨州）如图，，点是内的定点且，若点、分别是射线、上异于点的动点，则周长的最小值是　　A． B． C．6 D．39．（2018•泸州）如图，等腰的底边，面积为120，点在边上，且，是腰的垂直平分线，若点在上运动，则周长的最小值为　　．10．（2017•南通）如图，矩形中，，，点，，，分别在矩形各边上，且，，则四边形周长的最小值为　　A． B． C． D．