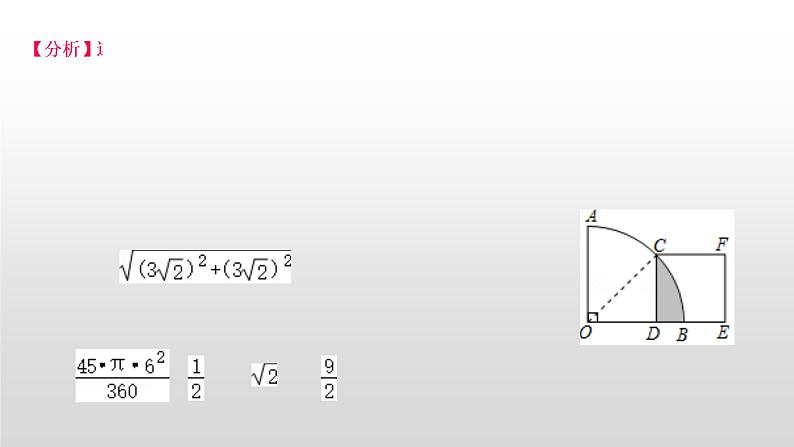
专题16【精品】 圆中求阴影部分的面积-2022年中考数学几何模型解题策略研究（课件+讲义）

专题16 圆中求阴影部分的面积

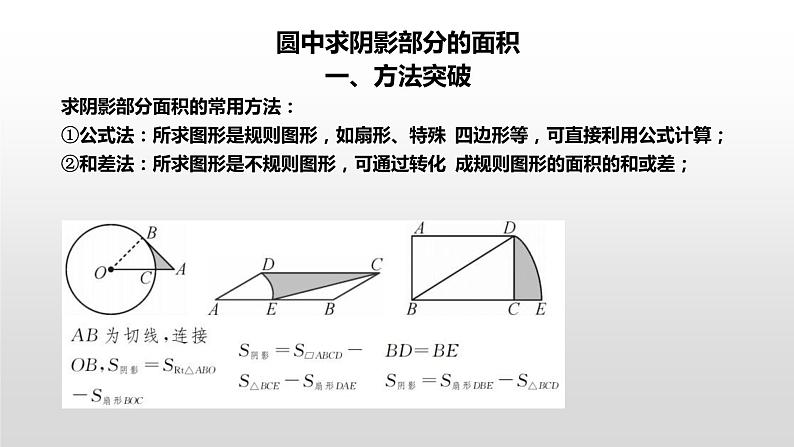
一、方法突破

求阴影部分面积的常用方法：

①公式法：所求图形是规则图形，如扇形、特殊 四边形等，可直接利用公式计算；

②和差法：所求图形是不规则图形，可通过转化 成规则图形的面积的和或差；

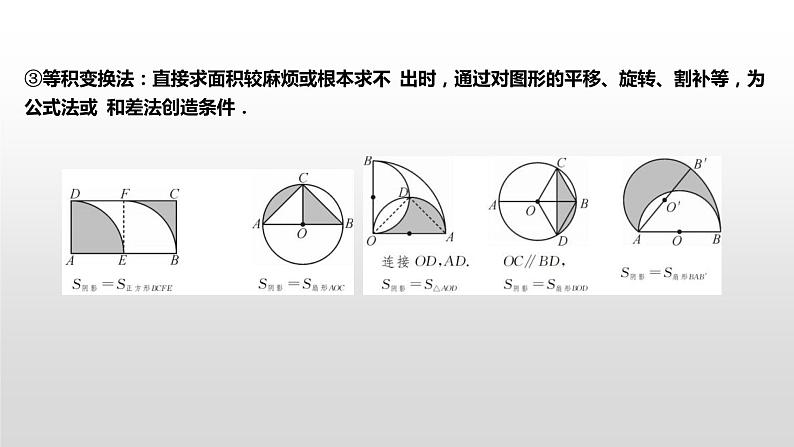
③等积变换法：直接求面积较麻烦或根本求不 出时，通过对图形的平移、旋转、割补等，为公式法或 和差法创造条件．

二、典例精析

类型1　公式法求面积

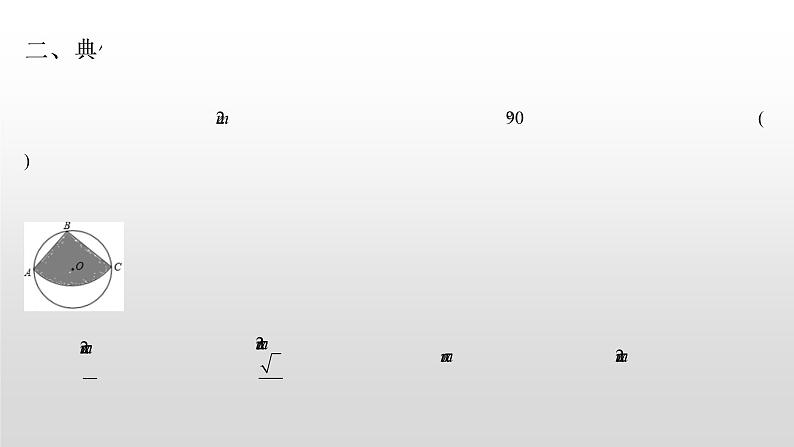
1．如图，从一块直径为的圆形铁皮上剪出一个圆心角为的扇形，则此扇形的面积为　　

A． B． C． D．

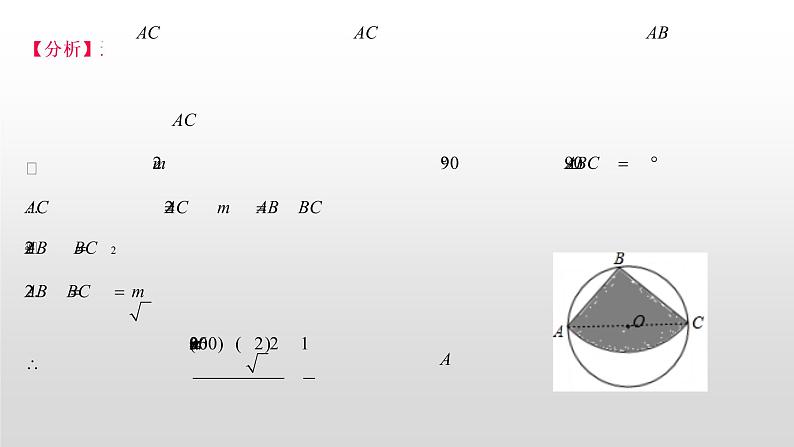
【分析】连接，根据圆周角定理得出为圆的直径，解直角三角形求出，根据扇形面积公式求出即可．

【解答】解：

连接，

从一块直径为的圆形铁皮上剪出一个圆心角为的扇形，即，

为直径，即，（扇形的半径相等），

，

，

阴影部分的面积是，

故选：．

类型2　和差法求面积

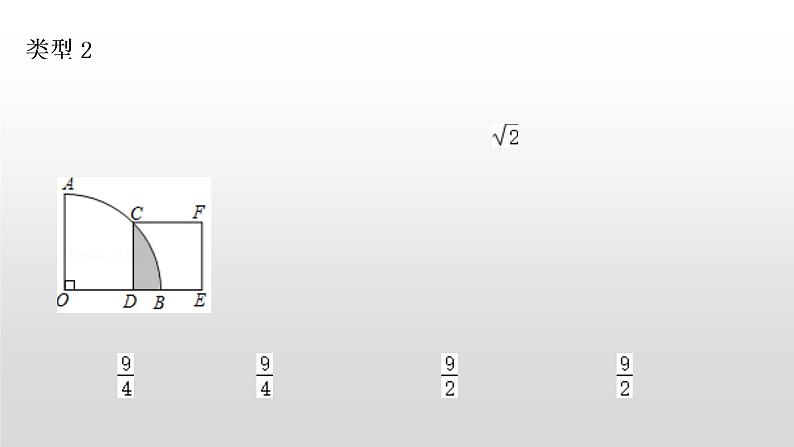
2．如图，在扇形AOB中，∠AOB＝90°，正方形CDEF的顶点C是的中点，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为3时，则阴影部分的面积为（　　）

A．18﹣π B．π﹣9 C．π﹣9 D．π﹣18

【分析】连接OC，根据勾股定理可求OC的长，根据题意可得出阴影部分的面积＝扇形BOC的面积﹣三角形ODC的面积，依此列式计算即可求解．

【解答】解：如图，连接OC，

∵在扇形AOB中∠AOB＝90°，正方形CDEF的顶点C是的中点，

∴∠COD＝45°，

∴OC＝＝6，

∴阴影部分的面积＝扇形BOC的面积﹣三角形ODC的面积

＝﹣×（3）2

＝π﹣9．

故选：C．

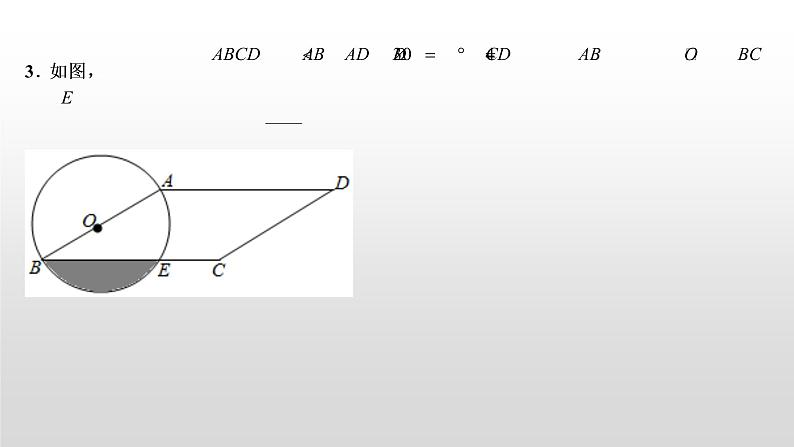
3．如图，在平行四边形中，，，，以为直径的交于点，则阴影部分的面积为　　．

【分析】连接半径和弦，根据直径所对的圆周角是直角得：，可得和的长，所以图中弓形的面积为扇形的面积与面积的差，因为，所以的面积是面积的一半，可得结论．

【解答】解：连接、，

是的直径，

，

四边形是平行四边形，

，，

，，

，

，

，

，

，

，

，

故答案为：．

4．如图，，，，为上一点，，以为圆心，以

为半径的圆与相切于点，与相交于点，连接、，则图中阴影部分的面积是　　．

【分析】根据扇形面积公式以及三角形面积公式即可求出答案．

【解答】解：，，

，

，

是等边三角形，

，

，

扇形的面积为：

为半径的圆与相切于点，

，

，

，

，

由勾股定理可知：

的面积为：

的面积为：，

阴影部分面积为：

故答案为：

5．如图，分别以边长为2的等边三角形的三个顶点为圆心，以边长为半径作弧，三段弧所围成的图形是一个曲边三角形，已知是的内切圆，则阴影部分面积为　　．

【分析】连接，作于，如图，利用等边三角形的性质得，，再根据三角形内切圆的性质得为的半径，，再计算出，，然后根据扇形的面积公式，利用阴影部分面积进行计算．

【解答】解：连接，作于，如图，

为等边三角形，

，，

是的内切圆，

为的半径，，

点为等边三角形的外心，

，

在中，，

，

阴影部分面积

．

故答案为．

类型3　整体思想求面积

6．如图，分别以五边形的顶点为圆心，以1为半径作五个圆，则图中阴影部分的面积之和为　　

A． B． C． D．

【分析】圆心角之和等于边形的内角和，由于半径相同，根据扇形的面积公式计算即可求出圆形中的空白面积，再用5个圆形的面积减去圆形中的空白面积可得阴影部分的面积．

【解答】解：边形的内角和，

圆形的空白部分的面积之和．

所以图中阴影部分的面积之和为：．

故选：．

7．如图，正六边形的边长为2，分别以正六边形的六条边为直径向外作半圆，与正六边形的外接圆围成的6个月牙形的面积之和（阴影部分面积）是　　

A． B． C． D．

【分析】图中阴影部分面积等于6个小半圆的面积和（大圆的面积正六边形的面积）即可得到结果．

【解答】解：6个月牙形的面积之和，

故选：．

8．把半径为1的圆分割成四段相等的弧，再将这四段弧依次相连拼成如图所示的恒星图形，那么这个恒星图形的面积等于　　．

【分析】恒星的面积边长为2的正方形面积半径为1的圆的面积，依此列式计算即可．

【解答】解：如图：

新的正方形的边长为，

恒星的面积．

故答案为．

类型4　利用等积转化法求面积

9．如图，等边三角形内接于，若的半径为2，则图中阴影部分的面积等于　　

A． B． C． D．

【分析】连接，如图，利用等边三角形的性质得，，然后根据扇形的面积公式，利用图中阴影部分的面积进行计算．

【解答】解：连接，如图，

为等边三角形，

，，

图中阴影部分的面积．

故选：．

10．如图，是的直径，弦，，，则阴影部分的面积为　　

A． B． C． D．

【分析】要求阴影部分的面积，由图可知，阴影部分的面积等于扇形的面积，根据已知条件可以得到扇形的面积，本题得以解决．

【解答】解：，

，

又弦，，

，

，

故选：．

11．运用图形变化的方法研究下列问题：如图，是的直径，、是的弦，且，，，．则图中阴影部分的面积是　　

A． B． C． D．

【分析】作直径，连接、、、，根据勾股定理求得的长，证明，则，然后根据三角形的面积公式证明，，则，即可求解．

【解答】解：作直径，连接、、、．

是圆的直径，

，则，

又，

，

，

，

，

，，

．

故选：．

12．如图，为半圆的直径，且，将半圆绕点顺时针旋转，点旋转到点的位置，则图中阴影部分的面积为　　．

【分析】根据图形可知，阴影部分的面积是半圆的面积与扇形的面积之和减去半圆的面积．

【解答】解：由图可得，

图中阴影部分的面积为：，

故答案为：．

13．如图，是半圆内一点，直径的长为，，，将绕圆心逆时针旋转至△，点在上，则边扫过的区域（图中阴影部分）的面积为　　

A． B． C． D．

【分析】根据已知条件和旋转的性质得出两个扇形的圆心角的度数，再根据扇形的面积公式进行计算即可得出答案．

【解答】解：，△是绕圆心逆时针旋转得到的，

，△，

，，

，

，

，，

，

，

，

阴影部分面积；

故选：．

三、中考真题演练

1．如图，已知的半径为1，是直径，分别以点、为圆心，以的长为半径画弧．两弧相交于、两点，则图中阴影部分的面积是　　

A． B． C． D．

【分析】连接、，如图，先判断为等边三角形，则，由于，所以图中阴影部分的面积，然后利用扇形的面积公式、等边三角形的面积公式和圆的面积公式计算．

【解答】解：连接，如图，

由作法可知，

为等边三角形，

，

，

图中阴影部分的面积

．

故选：．

2．如图，在矩形中，，，以点为圆心，长为半径画弧交于点，连接，则阴影部分的面积为　　

A． B． C． D．

【分析】根据矩形的性质得出，，求出，再分别求出扇形和矩形、的面积，即可得出答案．

【解答】解：四边形是矩形，，

，，

，

，

，，

，

阴影部分的面积

．

故选：．

3．如图，两个半径长均为的直角扇形的圆心分别在对方的圆弧上，扇形的圆心是的中点，且扇形绕着点旋转，半径、交于点，半径、交于点，则图中阴影面积等于　　

A． B． C． D．

【分析】根据扇形的面积公式求出面积，再过点作，作，垂足分别为、，然后证明与全等，从而得到中间空白区域的面积等于以为对角线的正方形的面积，从而得出阴影部分的面积．

【解答】解：两扇形的面积和为：，

过点作，作，垂足分别为、，

则四边形是矩形，

点是的中点，

平分，

，

矩形是正方形，

，，

，

在与中，

，

，

中间空白区域面积相当于对角线是的正方形面积，

空白区域的面积为：，

图中阴影部分的面积两个扇形面积和个空白区域面积的和．

故选：．

4．如图，正方形的边长为2，为对角线的交点，点，分别为，的中点．以为圆心，2为半径作圆弧，再分别以，为圆心，1为半径作圆弧，，则图中阴影部分的面积为　　

A． B． C． D．

【分析】连接，根据在同圆或等圆中，相等的圆心角所对的弧，所对的弦分别相等，利用面积割补法可得阴影部分的面积等于弓形面积，即等于扇形减去直角三角形的面积之差．

【解答】解：连接，，如图，

正方形的边长为2，为对角线的交点，

由题意可得：，经过点，且，．

点，分别为，的中点，

，

，．

弓形弓形．

阴影部分的面积等于弓形的面积．

．

故选：．

5．如图，在中，，，，以点为圆心，的长为半径画弧，交于点，交于点，以点为圆心，的长为半径画弧，交于点，交于点，则图中阴影部分的面积为　　

A． B． C． D．

【分析】先根据直角三角形中的勾股定理求得，再将求不规则的阴影部分面积转化为求规则图形的面积：，将相关量代入求解即可．

【解答】解：根据题意可知，则，

设，，

，

，即，

，

故选：．

6．如图，在菱形中，，，以为圆心、长为半径画，点为菱形内一点，连接，，．当为等腰直角三角形时，图中阴影部分的面积为　　

A． B． C． D．

【分析】连接，延长，交于，根据菱形的性质得出是等边三角形，进而通过三角形全等证得，从而求得、，利用即可求得．

【解答】解：连接，延长，交于，

在菱形中，，，

，，

是等边三角形，

，

在和中，

，

，

，

，，

为等腰直角三角形，

，

在中，，

，

，

故选：．

7．如图，在中，，以为直径的分别与，交于点，，过点作，垂足为点，若的半径为，，则阴影部分的面积为　　

A． B． C． D．

【分析】连接，，先通过直径所对是圆周角是直角，证出，从而得出，再通过计算即可．

【解答】解：连接，

为直径，

，

，

，

，

，

，

，

，

，，

，

，

，

，

作于，

在中，，

，

，

，

．

故选：．

8．如图，直线与坐标轴交于、两点，点是线段上的一个动点，过点作轴的平行线交直线于点，绕点顺时针旋转，边扫过区域（阴影部分）面积的最大值是　　

A． B． C． D．

【分析】设，则，根据图形可表示出扫过区域（阴影部分）面积是两个扇形面积之差，将面积表示出来，利用二次函数性质即可求最大值．

【解答】解：设，则．

，．

绕点顺时针旋转．

，．

扫过区域（阴影部分）面积．

当时，的最大值为：．

故选：．

9．如图，，，两两不相交，且半径都等于2，则图中三个扇形（即阴影部分）的面积之和为 　　．（结果保留

【分析】】根据三个扇形的半径都是2，由扇形的面积公式即可求出阴影部分的面积．

【解答】解：三个扇形的半径都是2，

而三个圆心角的和是，

图中的三个扇形（即三个阴影部分）的面积之和为．

故答案为：．

10．如图，作的任意一条直径，分别以、为圆心，以的长为半径作弧，与相交于点、和、，顺次连接、、、、、，得到六边形，则的面积与阴影区域的面积的比值为 　　．

【分析】连接，，将图中阴影部分面积拼补为与面积之和，进一步确定、是正三角形，从而求出阴影部分的面积，即可求解．

【解答】解：连接，，

设的半径为，

的面积，

弓形，的面积与弓形，的面积相等，

弓形，的面积与弓形，的面积相等，

图中阴影部分的面积，

，

、是正三角形，

阴影部分的面积，

的面积与阴影区域的面积的比值为，

故答案为：．

11．如图，在中，为的中点，以为圆心，长为半径画弧交对角线于点，若，，，则扇形的面积为 　　．

【分析】根据三角形内角和定理求出，根据三角形的外角的性质求出，根据扇形面积公式计算．

【解答】解：，，

，

又为的中点，

，

，

，

，

，

扇形的面积，

故答案为：．

12．如图，是的弦，，点是上的一个动点，且，若点，分别是，的中点，则图中阴影部分面积的最大值是 　　．

【分析】连接、、，根据圆周角定理得到，求出，，再根据三角形中位线性质得到，，然后根据三角形相似得到，故当的面积最大时，的面积最大，由、、在一条直线时，的面积最大，求得的最大值，进而即可求得的面积最大值，利用扇形的面积和三角形的面积求得弓形的面积，进而即可求得阴影部分的最大值．

【解答】解：连接、、，如图，

，

，

，

，

，

，

，

，

，

点、分别是、的中点，

，，

，

，

当的面积最大时，的面积最大，

、、在一条直线时，的面积最大，

的面积最大值为：，

的面积最大值为：，

，

此时，，

故答案为：．

13．如图，等腰直角三角形中，，．分别以点、点为圆心，线段长的一半为半径作圆弧，交、、于点、、，则图中阴影部分的面积为 　　．

【分析】阴影部分的面积等于的面积减去空白处的面积即可得出答案．

【解答】解：等腰直角三角形中，，，

，

，

阴影部分的面积，

故答案为．

14．如图，正方形的边长为2，分别以，为圆心，以正方形的边长为半径的圆相交于点，那么图中阴影部分的面积为 　　．

【分析】连接、，作于，根据等边三角形的性质得到，解直角三角形求出、，根据扇形面积公式、三角形的面积公式计算，得到答案．

【解答】解：连接、，作于，

，

为等边三角形，

，，

，，

则图中阴影部分的面积扇形的面积（扇形的面积的面积）

，

故答案为：．

15．如图，在边长为4的正方形中，以为直径的半圆交对角线于点，以为圆心、长为半径画弧交于点，则图中阴影部分的面积是 　　．

【分析】根据扇形的面积公式和三角形面积公式即可得到结论．

【解答】解：连接，

为直径，

，

，，

，

，

图中阴影部分的面积

，

故答案为．

16．如图，将绕点顺时针旋转得到△，已知，，则线段扫过的图形（阴影部分）的面积为　　．

【分析】根据图形可以得出扫过的图形的面积，由旋转的性质就可以得出就可以得出扫过的图形的面积求出其值即可．

【解答】解：绕点旋转得到△，

△，

，．

扫过的图形的面积，

扫过的图形的面积，

扫过的图形的面积．

故答案为：．