初中数学华师大版八年级下册2. 函数的图象教案

函数的图象

一、 教材分析

《函数的图像》是在学习函数概念的基础上，进一步讨论函数的图象，学习从函数图象上获取信息和函数的图象画法，初步讨论函数的变化规律和变化趋势。同时这节课对于学习函数，培养学生的探索能力，拓展学生的空间想象力也有十分重要的意义。

二、教学目标

1.知识与技能

（1）学会用列表、描点、连线画函数图象。

（2）学会观察、分析函数图象获取信息。

2.过程与方法

（1）提高识图能力、分析函数图像信息能力。

（2）经历画函数图象的过程，体会数形结合思想，并利用它解决问题，提高解决问题能力。

3.情感、态度与价值观

（1）体会数学方法的多样性，提高学习兴趣。

（2）认识数学在解决问题中的重要作用。

三、教学重点

1.函数图象的画法。

2.观察分析图象获取信息。

四、教学难点

分析概括图象信息。

五、学情分析

八年级下学期的学生具有初步的识图能力，但他们的几何认知能力仍处于较低级的阶段，空间观念、想象力还需要进一步提高。对函数图象的解读，也会出现各种各样的问题，另外在实践能力和综合应用等方面也还需要加强。根据自主性和差异性原则，把学法概括为“感，探，议，创”从学生感兴趣的问题情境感知函数图象，引导学生自主探究，并在合作交流的基础上创造性学习。

六、教法与学法

自主探究、合作交流、归纳总结。

七、教学准备

教师：三角尺，多媒体课件。

学生：作图工具，方格子纸。

八、学习过程

（一）新课引入

在平面直角坐标系中，平面内的点可以用一对（有序数对）来表示。即坐标平面内的（点）与有序数对是一一（对应）的。

（二）学习目标

1.了解函数图象的意义。

2.学会用列表、描点、连线画函数图象;学会观察、分析函数图象获取信息。

3.体会函数图象建立数形联系的关键是分别用点的横、纵坐标表示自变量和对应的函数值。

（三）研读课文

认真阅读课本第75至77页的内容，思考以下问题：

1.什么是函数图像?

2.如何作函数图像？具体步骤有哪些？

3.如何判定一个图像是函数图像，你判断的依据是什么?

（四）合作探究

知识点一   函数的图像

问题：写出正方形的面积S与边长x的函数解析式，并确定自变量x的取值范围。

生：S=x2 （x＞0）

师：你能解释x＞0这个范围是怎样确定的吗？

生：因为x表示的实际含义是正方形的边长，边长只能为正。

画函数图像的三个步骤

师：刚才同学们进行了自学，请回答画函数图像的三个步骤

生：(1)列表、(2) 描点、（3）连线。

下面我们画函数S=x2 （x＞0）的图象

（1）列表：（计算并填写下表）

（2）描点：（建立直角坐标系，以所填表格中的自变量x的值作为横坐标，相对应的函数值S作为纵坐标，即可在坐标系中得到一些点，描出表格中数值对应的各点）

（学生在方格子纸上建立直角坐标系并按照列表中的有序数对进行描点，同时教师利用多媒体课件演示）

（3）连线：（按照横坐标由小到大的顺序，把所描出的各点用平滑曲线连接起来）

想一想：这条曲线包括原点吗？应该怎样表示？

强调：用表示不在曲线上的点；在函数图象上的点要画成的点．

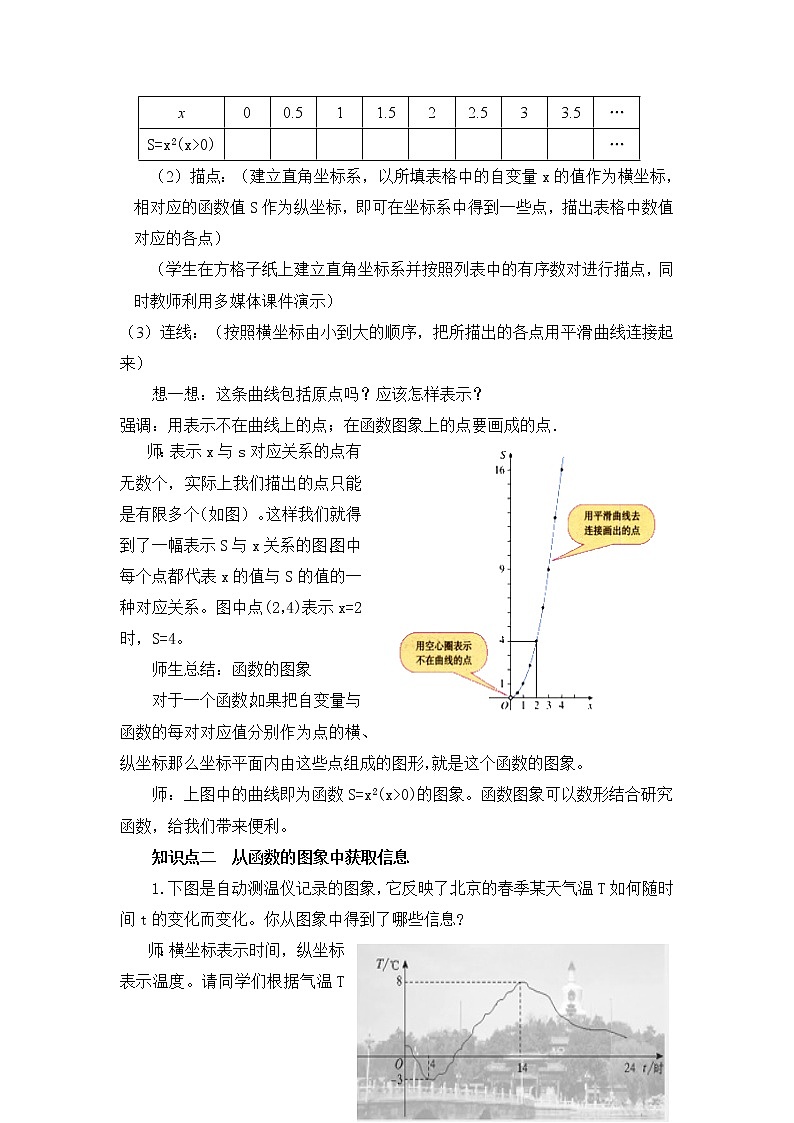
师：表示x与s对应关系的点有无数个，实际上我们描出的点只能是有限多个（如图）。这样我们就得到了一幅表示S与x关系的图，图中每个点都代表x的值与S的值的一种对应关系。图中点(2，4)表示x=2时，S=4。

师生总结：函数的图象

对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象。

师：上图中的曲线即为函数S=x2(x>0)的图象。函数图象可以数形结合研究函数，给我们带来便利。

知识点二  从函数的图象中获取信息

1.下图是自动测温仪记录的图象，它反映了北京的春季某天气温T如何随时间t的变化而变化。你从图象中得到了哪些信息?

师：横坐标表示时间，纵坐标表示温度。请同学们根据气温T 随时间t变化而变化的规律回答:

（1）哪个时间温度最高?是多少度?

（2）哪个时间温度最低?是多少度?

（3）什么时间段温度在下降?什么时间段温度在上升?

（4）曲线与x轴的交点表示什么?

（5）温度在零度以下的时间长还是在零度以上的时间长?

学生交流回答。

2.下图反映的过程是小明从家去食堂吃早餐，接着去图书馆读报，然后回

家．其中x表示时间，y表示小明离家的距离，小明家、食堂、图书馆在同一直线上．根据图象回答下列问题：  （1）食堂离小明家多远？小明从家到食堂用了多少时间？  （2）小明在食堂吃早餐用了多少时间？

（3）食堂离图书馆多远？小明从食堂到图书馆用了多少时间？（4）小明读报用了多长时间？

（5）图书馆离小明家多远？小明从图书馆回家的平均速度是多少？生：结合图象解答问题。

（五）强化训练

1.点P（2，5）（填“在”或“不在”）函数y=2x的图象上.

2.下面的图象反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家，图中x表示时间，y表示张强离家的距离.

（1）体育场离张强家多远？张强从家到体育场用了多少时间？

（2）体育场离文具店多远？

（3）张强在文具店停留了多少时间？

（4）张强从文具店回家的平均速度是多少？

（学生独立解答，教师巡视指导）

（六）课堂小结

1.函数图象的意义。

2.用描点法画函数图象按照哪些步骤进行？

3.通过图象可以数形结合地研究函数。

（七）达标测试

1.如图，某天小明骑自行车上学，途中因自行车发生故障，修车耽误了一段时间后继续骑行，按时赶到了学校.右图描述了他上学的情景，下列说法中错误的是（     ）

A．修车时间为15分钟

B．学校离家的距离为2000米

C．到达学校时共用时间20分钟

D．自行车发生故障时离家距离为1000米

2.由于干旱，某水库的蓄水量随时间的增加而直线下降．若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示，则下列说法正确的是(  )．

A．干旱开始后，蓄水量每天减少20万米3

B．干旱开始后，蓄水量每天增加20万米3

C．干旱开始时，蓄水量为200万米3

D．干旱第50天时，蓄水量为1 200万米3

3.小高从家门口骑车去单位上班，先走平路到达点A，再走上坡路到达点B，最后走下坡路到达工作单位，所用的时间与路程的关系如图所示．下班后，如果他沿原路返回，且走平路、上坡路、下坡路的速度分别保持和去上班时一致，那么他从单位到家门口需要的时间是多少？

4．某运动员将高尔夫球击出，描绘高尔夫球击出后离原处的距离与时间的函数关系的图像可能为（   ）．

5、假定甲、乙两人在一次赛跑中，路程S与时间T的关系在平面直角坐标系中所示，如图，请结合图形和数据回答问题：

（1）这是一次米赛跑；

（2）甲、乙两人中先到达终点的是；

（3）乙在这次赛跑中的速度为多少米/秒？

 (4)甲到达终点时，乙离终点还有　　　　米

板书设计

函数的图象

1.函数图象的定义：                 学生板演画函数图象      

2.画函数图象的步骤:

（1）列表

（2）描点

（3）连线                 

3.看函数图象的方法

设计思想

本课设计的学习内容都是学生所熟知的或发生在身边的事实，情景导入是从已有的知识出发引导学生研读课文内容，明确学习目标。在知识探究中，首先通过再现学生熟悉的正方形的面积S与边长x的关系S=x2 （x＞0），帮助学生在自主探究与合作交流的过程中由列表、描点、连线来探究函数的图象并理解函数图象的意义。从函数的图象中获取信息，也是由实例入手，通过一些现实生活中用图象来反映的问题实例，让学生经历将实际问题抽象为数学问题的过程．教学生如何观察分析图象，学会观察图象的一般步骤，利用“问题串”的形式引导学生逐步深入获得图象所传达的信息，逐步熟悉图象语言。