备战2022年中考数学冲刺复习——二次函数的图象与性质 课件

这是一份备战2022年中考数学冲刺复习——二次函数的图象与性质 课件，共30页。PPT课件主要包含了答案显示，y1＞y2＞y3，见习题，答案C，答案A等内容，欢迎下载使用。

1．二次函数y＝2(x－6)2＋9图象的顶点坐标是(　　)A．(－6，9) B．(6，9) C．(6，－9) D．(－6，－9)
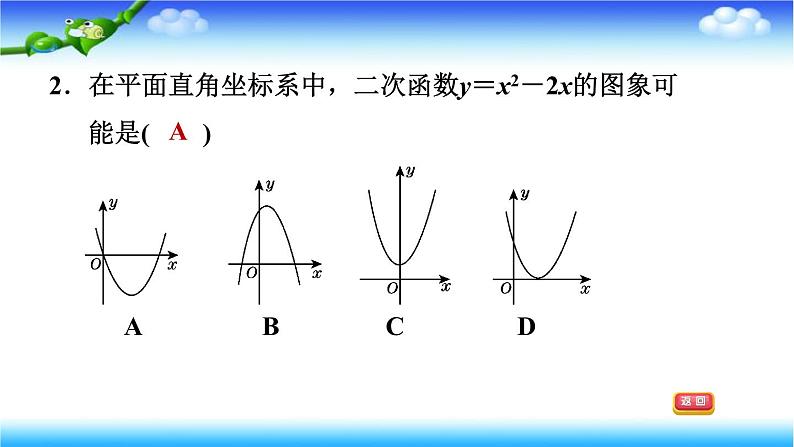
2．在平面直角坐标系中，二次函数y＝x2－2x的图象可能是(　　)
A B C D
3．对于二次函数y＝x2－2x－8，下列描述错误的是(　　)A．其图象的对称轴是直线x＝1 B．其图象的顶点坐标是(1，－9) C．当x＝1时，y有最小值－8 D．当x＞1时，y随x的增大而增大
4．【2021·泉州模拟】已知二次函数y＝ax2－2ax＋3(a>0)，当0≤x≤m时，3－a≤y≤3，则m的取值范围为(　　)A．0≤m≤1 B．0≤m≤2C．1≤m≤2 D．m≥2
【点拨】二次函数y＝ax2－2ax＋3＝a(x－1)2＋3－a(a>0)，∴该函数图象开口向上，对称轴是直线x＝1，当x＝1时，该函数取得最小值，最小值为3－a，∵当0≤x≤m时，3－a≤y≤3，且当y＝3时，x＝2或x＝0，∴1≤m≤2，故选C.
5．如图，抛物线y＝ax2＋bx＋c的对称轴为直线x＝－1，且过点 ，有下列结论：①abc＞0；②a－2b＋4c＝0；③25a－10b＋4c＝0；④3b＋2c＞0；⑤b2＞4ac.其中正确的结论有(　　)A．①③⑤ B．①②⑤ C．①④⑤ D．③④⑤
∵抛物线与x轴有两个交点，∴b2－4ac＞0，∴b2＞4ac，故⑤正确．故选A.
6．若二次函数y＝x2－4x＋c的图象经过点(0，2)，则函数y的最小值是________．
7．设A(－2，y1)，B(1，y2)，C(2，y3)是抛物线y＝－(x＋1)2＋a上的三点，则y1，y2，y3的大小关系为______________．
8．【2021·安徽】设抛物线y＝x2＋(a＋1)x＋a，其中a为实数．(1)若抛物线经过点(－1，m)，则m＝________；(2)将抛物线y＝x2＋(a＋1)x＋a向上平移2个单位，所得抛物线顶点的纵坐标的最大值是________．
9．【2021·龙岩模拟改编】抛物线y＝－4x2＋8mx＋3与x轴交于点A，B(其中点A在点B的左边)，与y轴交于点C，AB＝2，在y轴上取点D(0，1)，连结AD，BC，则AD＋BC的最小值为________．
10．已知二次函数y＝2x2＋4x＋3，当－2≤x≤1时，求函数y的最小值和最大值．下面是小明同学的解答过程．你认为他的解答正确吗？如果正确，请说明解答依据；如果不正确，请写出你的解答过程．解：当x＝－2时，y＝2×(－2)2＋4×(－2)＋3＝8－8＋3＝3.当x＝1时，y＝2×12＋4×1＋3＝2＋4＋3＝9.∴y的最大值是9，最小值是3.
解：小明的解答不正确．正确的解答如下：∵二次函数y＝2x2＋4x＋3＝2(x＋1)2＋1，∴该函数图象开口向上，对称轴是直线x＝－1，当x＝－1时，y取得最小值，最小值是1，∵－2≤x≤1，∴当x＝1时，y取得最大值，此时y＝9.当x＝－1时，y取得最小值，此时y＝1，由上可得，当－2≤x≤1时，函数y的最小值是1，最大值是9.
11．【2021·开福区模拟】定义：对于给定的两个函数，任取自变量x的一个值，当x<0时，它们对应的函数值互为相反数；当x≥0时，它们对应的函数值相等，我们称这样的两个函数互为相关函数，例如：一次函数y＝x－1，它的相关函数为y＝
(1)已知点A(－5，8)在一次函数y＝ax－3的相关函数的图象上，求a的值；
②当－3≤x≤3时，求函数y＝－x2＋4x－ 的相关函数的最大值和最小值．
12．如图，在平面直角坐标系中，抛物线过A(－1，3)，B(4，8)，O(0，0)三点．(1)求该抛物线和直线AB的表达式．
(2)平移抛物线，求同时满足以下两个条件的平移后的抛物线的表达式：①平移后抛物线的顶点在直线AB上；
②设平移后抛物线与y轴交于点C，S△ABC＝3S△ABO.
解：当x＝0时，y＝x＋4＝4，则直线AB与y轴的交点坐标为(0，4)，设平移后抛物线的顶点坐标为(t，t＋4)，则平移后的抛物线的表达式为y＝(x－t)2＋t＋4，