鲁教版 (五四制)七年级下册2 等腰三角形教案设计

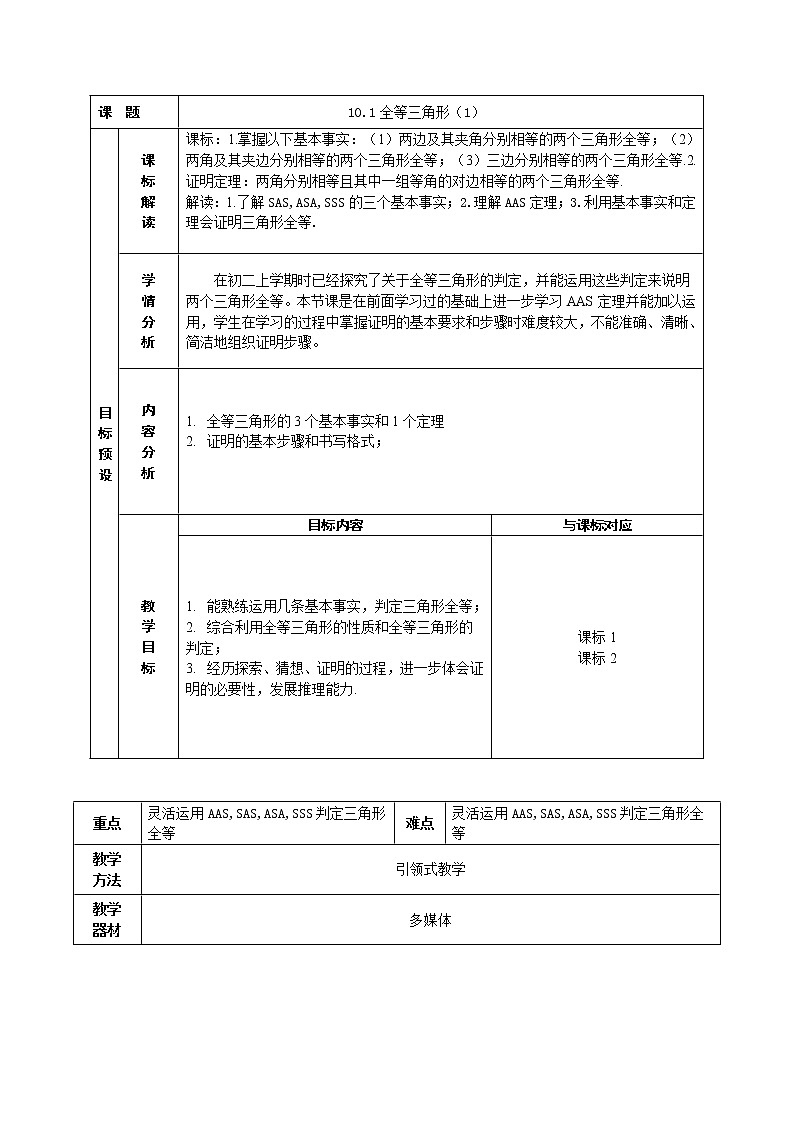
这是一份鲁教版 (五四制)七年级下册2 等腰三角形教案设计，共4页。教案主要包含了全等三角形的基本事实，定理AAS的证明，应用等内容，欢迎下载使用。
,
课 题
10.1全等三角形（1）
目
标
预
设
课
标
解
读
课标：1.掌握以下基本事实：（1）两边及其夹角分别相等的两个三角形全等；（2）两角及其夹边分别相等的两个三角形全等；（3）三边分别相等的两个三角形全等.2.证明定理：两角分别相等且其中一组等角的对边相等的两个三角形全等.
解读：1.了解SAS,ASA,SSS的三个基本事实；2.理解AAS定理；3.利用基本事实和定理会证明三角形全等.
学
情
分
析
在初二上学期时已经探究了关于全等三角形的判定，并能运用这些判定来说明两个三角形全等。本节课是在前面学习过的基础上进一步学习AAS定理并能加以运用，学生在学习的过程中掌握证明的基本要求和步骤时难度较大，不能准确、清晰、简洁地组织证明步骤。
内
容
分
析
全等三角形的3个基本事实和1个定理
证明的基本步骤和书写格式；
教
学
目
标
目标内容
与课标对应
能熟练运用几条基本事实，判定三角形全等；
综合利用全等三角形的性质和全等三角形的判定；
经历探索、猜想、证明的过程，进一步体会证明的必要性，发展推理能力.
课标1
课标2
重点
灵活运用AAS,SAS,ASA,SSS判定三角形全等
难点
灵活运用AAS,SAS,ASA,SSS判定三角形全等
教学
方法
引领式教学
教学
器材
多媒体
巩固
练习 与 知识 铺垫
∵△ABC≌△DEF，∴ .
全等三角形的判定有哪些？
命题证明的步骤是什么？（1） （2） （3）
操作方法：组员之间进行交流讨论，学生代表进行发言.
新课
引入
在《平行线的有关证明》一章中，我们给出了八条基本事实，并从其中的几条基本事实出发证明了有关平行线的一些结论.运用这些基本事实和已经学习过的定理，我们还可以证明有关三角形的一些结论.
新
课
教
学
一、全等三角形的基本事实
基本事实1. 的两个三角形全等.（SAS）
基本事实2. 的两个三角形全等.（ASA）
基本事实3. 的两个三角形全等.（SSS）
由上面的基本事实，可以证明许多几何结论.
二、定理AAS的证明
我们已经探索过“两角分别相等且其中一组等角的对边相等的两个三角形全等”这个结论，你能用有关的基本事实和已经证明过的定理证明它吗？
已知：如图，在△ABC和△A′B′C′中，∠B = ∠B′,∠C=∠C′,AB=A′B′.
求证：△ABC≌△A′B′C′
A A′
B C B′ C′
证明：∵∠A+∠B+∠C=180°,∠A′+∠B′+∠C′=180°
∴∠A=180°-∠B-∠C,∠A′=180°-∠B′-∠C′
新
课
教
学
∵∠B=∠B′,∠C=∠C′
∴∠A=∠A′.
在△ABC和△A′B′C′中
∠A=∠A′
AB=A′B′
∠B=∠B′
∴△ABC≌△A′B′C′（ASA）
操作方法：教师引领学生分析上述结论，写出已知求证，根据已知求证形成解题思路，学生书写解题过程.
由此可以得到下面的定理：
定理 两角分别相等且其中一组等角的对边相等的两个三角形全等.（AAS）
定理巩固：如图，在△ABC和 △DEF中，AB=DE，∠B=∠E，添加哪些条件，可判断△ABC≌△DEF.
A D
B C E F
解：（1）应添加 ，使得△ABC≌△DEF（ ）
应添加 ，使得△ABC≌△DEF（ ）
（3）应添加 ，使得△ABC≌△DEF（ ）
三、应用
例1 已知：如图，线段AB和CD相较于点O，线段OA=OB,OC=OD.
求证：AC=BD,∠A=∠D.AD
O
证明：在△OAC和△ODB中，
OA=OD
∠AOC==∠DOB
OC=OB
∴△OAC≌△ODB（SAS） C B
∴AC=BD，∠A=∠D（全等三角形的定义）
操作方法：教师引领学生分析题意，形成解题思路，学生整理思路上台展示.
练习：完成下面的证明过程.
已知：如图，AB与CD相交于点O，△AOC≌△DOB.
求证：△ABD≌△DCA. A D
O

C B

新
课
教
学
证明：∵△AOC≌△DOB
∴AO=DO,CO=BO，AC=DB（ ）.
∴ + = + ，
即AB=DC
在△ABD和△DCA中
DB=AC
=
=
∴△ABD≌△DCA（ ）
操作方法：学生自主审题理解题意，根据题意填写证明过程，小组之间进行交流讨论，学生代表回答
课
堂
小
结
全等三角形的的3个基本事实和1个定理的内容
证明的基本步骤和书写格式