初中数学鲁教版 (五四制)七年级下册第八章 平行线的有关证明4 平行线的判定定理教案配套课件ppt

这是一份初中数学鲁教版 (五四制)七年级下册第八章 平行线的有关证明4 平行线的判定定理教案配套课件ppt，共19页。PPT课件主要包含了“小小工程师”，第一关，第二关，谢谢指导，ABCD，平角的定义，平行线的判定等内容，欢迎下载使用。

8.4平行线的判定定理
1.了解证明的基本步骤和书写格式。2.会根据已学的基本事实或定理来证明两直线平行。
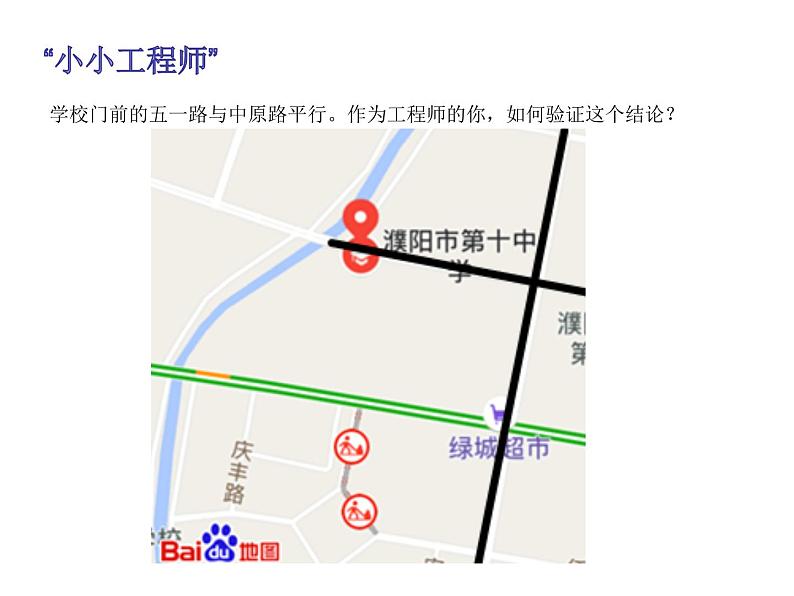
学校门前的五一路与中原路平行。作为工程师的你，如何验证这个结论？
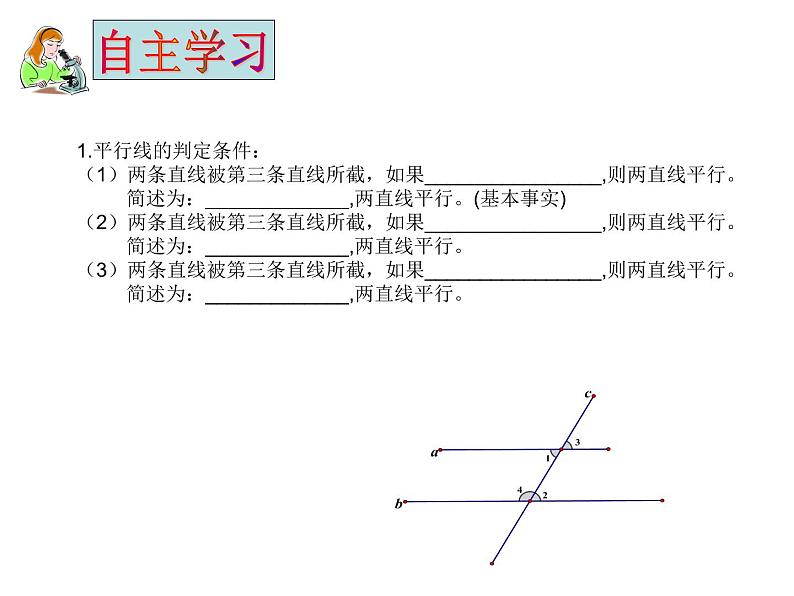
1.平行线的判定条件：（1）两条直线被第三条直线所截，如果________________,则两直线平行。 简述为：_____________,两直线平行。(基本事实)（2）两条直线被第三条直线所截，如果________________,则两直线平行。 简述为：_____________,两直线平行。（3）两条直线被第三条直线所截，如果________________,则两直线平行。 简述为：_____________,两直线平行。
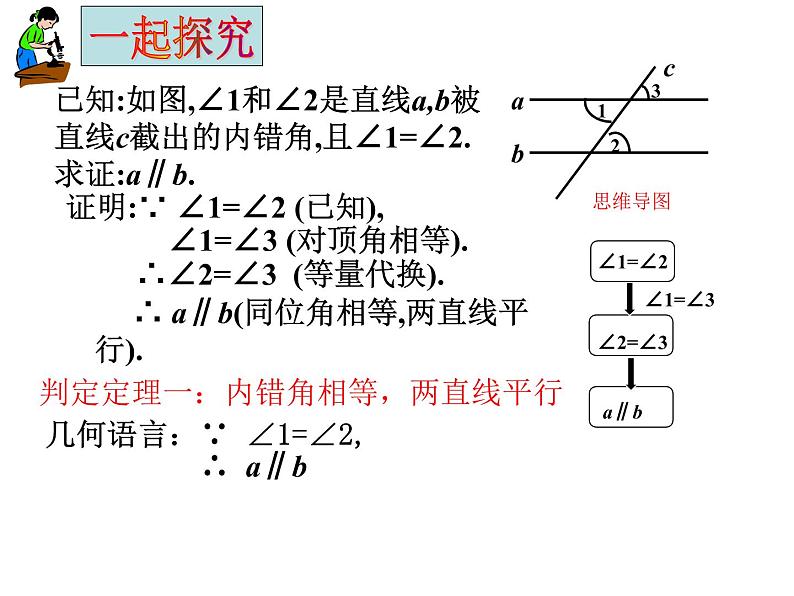
已知:如图,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2.求证:a∥b.
证明:∵ ∠1=∠2 (已知),
∠1=∠3 (对顶角相等).
∴∠2=∠3 (等量代换).
∴ a∥b(同位角相等,两直线平行).
判定定理一：内错角相等，两直线平行
几何语言：∵ ∠1=∠2, ∴ a∥b
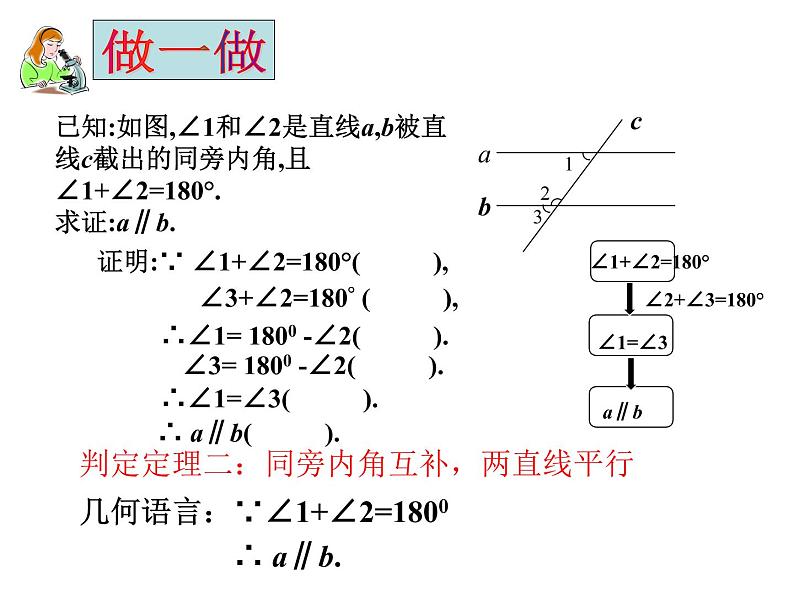
已知:如图,∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1+∠2=180°.求证:a∥b.
证明:∵ ∠1+∠2=180°( ),
∠3+∠2=180° ( ),
∠3= 1800 -∠2( ).
∴∠1=∠3( ).
∴ a∥b( ).
∴∠1= 1800 -∠2( ).
判定定理二：同旁内角互补，两直线平行
几何语言：∵∠1+∠2=1800 ∴ a∥b.
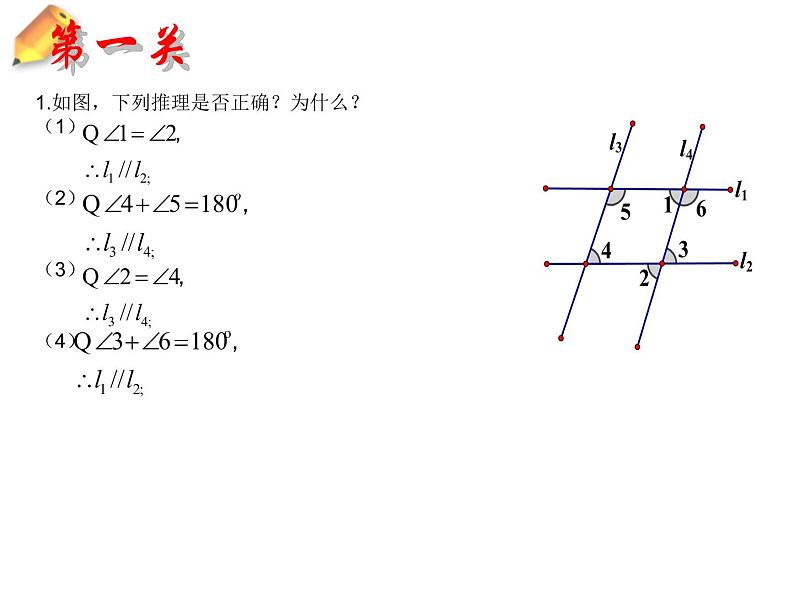
1.如图，下列推理是否正确？为什么？（1）（2）（3）（4）
已知：如图，直线a,b被直线c所截。且∠1+ ∠2=180°求证：a∥b.你有几种证明方法？
已知，如图，BP交CD于点P, ∠ABP+∠BPC=180 º. 求证：EB∥PF
如图：直线AB、CD都和AE相交，且∠1+∠A=180º ．求证：AB//CD
（ ）
同旁内角互补，两直线平行
证明：∵∠1+∠3=180 º（平角的定义） ∠2+∠3=180 º（ ）
以下是小明利用三角板和直尺做已知直线的平行线的方法，他做的对吗？依据是什么？
小杰用如图所示的方法作出了平行线,你认为他的作法对吗?为什么?
通过这个操作活动,得到了什么结论?
公理:同位角相等,两直线平行. ∵ ∠1=∠2, ∴ a∥b.
判定定理1:内错角相等,两直线平行.∵ ∠1=∠2, ∴ a∥b.
判定定理2:同旁内角互补,两直线平行. ∵∠1+∠2=1800 , ∴ a∥b.
这里的结论,以后可以直接运用.
　　已知：如图，在△ABC中，∠A=38°，BC边绕点C按逆时针方向旋转一周回到原来的位置．在旋转的过程中，是否有某一位置使CB′∥AB ？如果有这样的位置，请你画出示意图，并写出判断它们平行的理由．
平行线判定定理一 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.(简记为:内错角相等,两直线平行)