初中数学人教版七年级上册第一章 有理数1.4 有理数的乘除法1.4.2 有理数的除法优秀ppt课件

这是一份初中数学人教版七年级上册第一章 有理数1.4 有理数的乘除法1.4.2 有理数的除法优秀ppt课件，文件包含142《有理数的除法》课件pptx、142《有理数的除法》教案docx等2份课件配套教学资源，其中PPT共24页， 欢迎下载使用。

有理数的除法及分数化简
【思考】我们在前面学习有理数的减法时，是借助于逆运算把它转化为加法来进行的.大家知道除法的逆运算是乘法，那么有理数的除法运算是不是也可以借助于逆运算转化为乘法来进行呢？
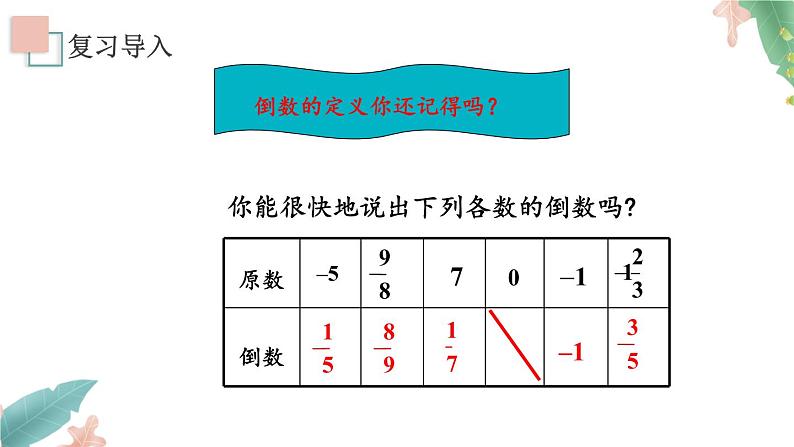
你能很快地说出下列各数的倒数吗?
8÷(–4)=___ (–36)÷6= ___ =___ (–72)÷9=___
(–4)×(–2)=8 6×(–6)= –36 (–8)×9= –72
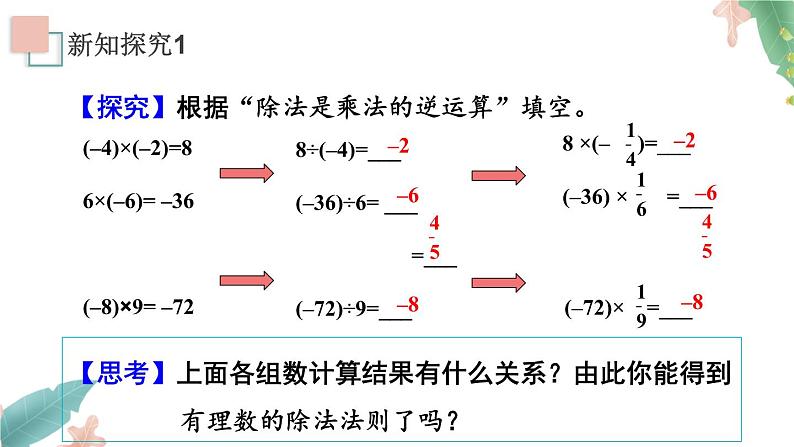
【探究】根据“除法是乘法的逆运算”填空。
8 ×(– )=___
(–36) × =___
(–72)× =___
【思考】上面各组数计算结果有什么关系？由此你能得到有理数的除法法则了吗？
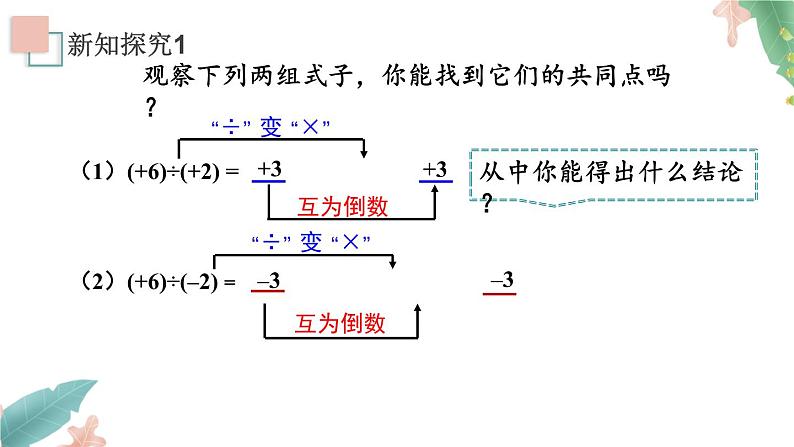
观察下列两组式子，你能找到它们的共同点吗？
从中你能得出什么结论？
有理数除法法则（一）
除以一个不等于0的数，等于乘这个数的倒数。
利用上面的除法法则计算下列各题。（1）(–54)÷ (–9)； （2）(–27) ÷3；（3）0 ÷ (–7)； （4）(–24) ÷(–6)。
【思考】从上面我们能发现商的符号有什么规律？
两数相除，同号得正，异号得负，并把绝对值相除。 0除以任何一个不等于0的数，都得0。
到现在为止我们有了两个除法法则，那么两个法则是不是都可以用于解决两数相除呢？
1. 两个法则都可以用来求两个有理数相除。2. 如果两数相除，能够整除的就选择法则二，不能够整除的就选择用法则一。
1 计算（1）(–36) ÷ 9； （2） 。
解：（1）(–36) ÷ 9= –(36× )= –4； （2）
（1）24 ÷(-6)（2）(-4) ÷（3）0÷（4）( ) ÷( )
（1） ；（2） 。
解：（1） （2）
1. 化简：（1） = ÷ = . （2） = = = . （3） = _____.
(–30)÷(–45)
计算 （1） （2）
解：（1）原式= = = = =
如果有带分数，可以将带分数写成整数部分和分数部分的和，利用分配律进行运算，更加简便.
（2）原式= = 1
1. 有理数除法化为有理数乘法以后，可以利用有理数乘法的运算律简化运算。
2. 乘除混合运算往往先将除法化为乘法，然后确定积的符号，最后求出结果（乘除混合运算按从左到右的顺序进行计算）。
解：原式= = =
解：原式= = = =
3. 计算：(–12) ÷ 3=　 　。
2. (–21) ÷7的结果是（　 　） A．3 B．–3 C． D. –
有理数除法化为有理数乘法以后，可以利用有理数乘法的运算律简化运算.
乘除混合运算往往先将除法化为乘法，然后确定积的符号，最后求出结果（乘除混合运算按从左到右的顺序进行计算）.
1. 计算 2. 计算
解：原式= =
解：原式= =
3. 计算
解：原式= =
（1）若a，b互为相反数，且a ≠ b，则 =________；
（2）当a < 0时， =_______；
（3）若 ，则a，b的符号分别是__________。
（4）若–3x=12，则x =_____.