苏科版七年级下册第12章 证明综合与测试教案配套课件ppt

这是一份苏科版七年级下册第12章 证明综合与测试教案配套课件ppt，共13页。PPT课件主要包含了是真命题，是假命题，不是命题，2对顶角相等，结论这两个角相等，等量代换，交流展示，已知结论证明，度数之和是360°，三检测反馈等内容，欢迎下载使用。
一.基础训练1、下列语句中，是命题的为（　　）A、延长线段AB至C　　　　B、垂线段最短　C、过点O作直线a∥b　　　　D、锐角都相等吗2、下列命题是假命题的是（　　）A、若0＜b＜a，则a2＞b2　　　　　　B、相等的角是对顶角
C、若a＋b＝0，则a、b互为相反数　　D、两点之间线段最短
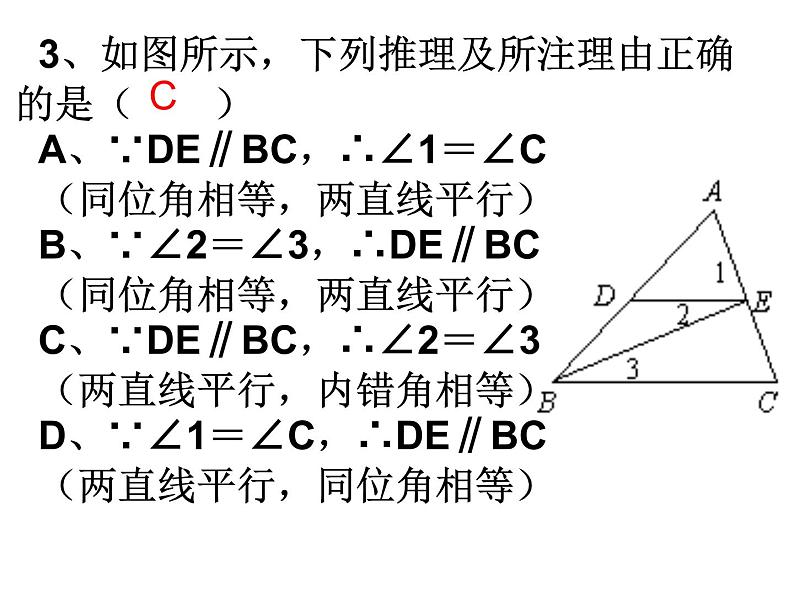
3、如图所示，下列推理及所注理由正确的是（　　）A、∵DE∥BC，∴∠1＝∠C（同位角相等，两直线平行）B、∵∠2＝∠3，∴DE∥BC（同位角相等，两直线平行）C、∵DE∥BC，∴∠2＝∠3（两直线平行，内错角相等）D、∵∠1＝∠C，∴DE∥BC（两直线平行，同位角相等）
4、对假命题举反例时，应注意使反例（　　）A、满足命题的条件，并满足命题的结论B、不满足命题的条件，但满足命题的结论C、不满足命题的条件，但也不满足命题的结论D、满足命题的条件，但不满足命题的结论
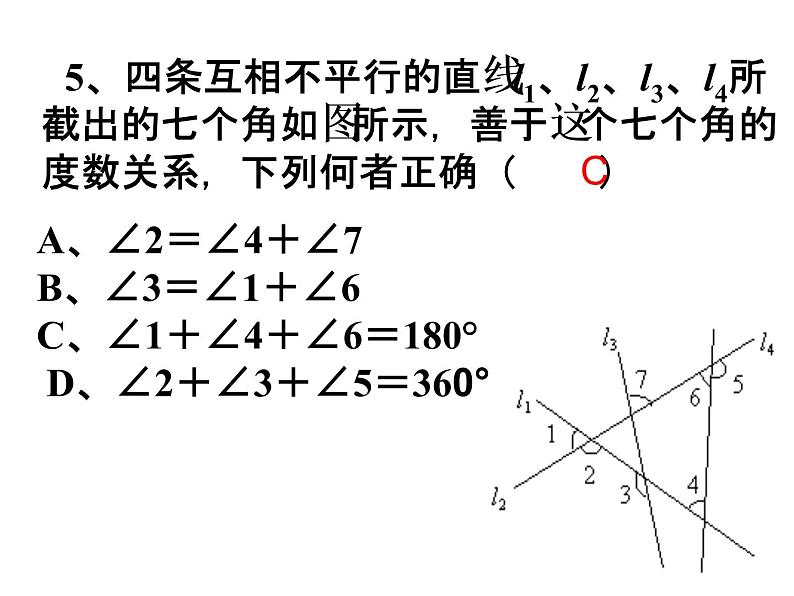
5、四条互相不平行的直线l1、l2、l3、l4所截出的七个角如图所示，善于这个七个角的度数关系，下列何者正确（　　）
A、∠2＝∠4＋∠7　　　　　B、∠3＝∠1＋∠6C、∠1＋∠4＋∠6＝180°　 D、∠2＋∠3＋∠5＝360° 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
专题复习一：命题与互逆命题
1.下列语句是不是命题？并判断其中命题的真假.
(1)在同一平面内，不相交的两条直线是平行线.(2)数学老师今年30岁.(3)如果a＞b， b＞c，那么a ＞c.(4)四边形不是多边形.
2.指出下列命题的条件和结论，并说出其逆命题.
(3)直角三角形的两个锐角互余.
(1)如果两个角的补角相等，那么这两个角相等.
逆命题:等角的补角相等.
条件:两个角是对顶角.
逆命题:有两个角互余的三角形是直角三角形.
逆命题:如果两个角相等，那么这两个角是对顶角.
专题复习二：平行线的判定和性质
例1:如图1,点A、B、C、D在一条直线上,填写下列空格:
∵EC∥FD ( 已知)∴∠F=∠ ( )又∵∠F=∠E (已知 )∴ ∠ = ∠E ( )∴ AE ∥BF ( )
请说出上面推理中应用了哪两个互逆的真命题.
两直线平行，内错角相等
内错角相等，两直线平行
如图3，从以下三个条件中 (1)AD∥BC(2)AB∥CD(3)∠A=∠C 任选两个作为条件，另一个做为结论， 构造一个命题，并证明其真假.
专题复习三：三角形内角和定理及推论
例2:如图4，已知BC⊥DE于点O，∠A=40°,∠D=30°, 求∠BED.
你还能求出哪些角的度数？
如图①，若AB∥CD，点P在AB、CD外部时,∠BPD、∠B、∠D有何数量关系？ 请证明你的结论.
（2）在图① 中，将点P移到AB、CD内部，请画出相应的图形，判断题（1）的结论还是否成立，若不成立，则∠BPD 、∠B、∠D之间有何数量关系？请证明你的结论.
∠B= ∠BPD+ ∠D
∠BPD = ∠B + ∠D
∠BPD+∠B+∠D= 360°
（3）在图②中，将直线AB绕点B逆时针方向旋转一定角度交 直线CD于点Q 如图④，则∠BPD 、 ∠B、 ∠D、∠BQD 之间 有何数量关系？
（4）根据（3）的结论求图⑤中∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的度数.
∠BPD= ∠B+∠D+∠BQD
2.下列命题：①偶数能被4整除 ； ②若a＞1且b＞1，则a＋b＞2；③平行同一直线的两直线平行，其中，逆命题正确的有（　　）A、1个　B、2个　C、3个　D、0个
3.如图，a∥b,等边三角形ABC的顶点B在直线b上，∠1=20°，则∠2的度数为（ ）A 60° B 45° C 40° D 30°
1.请写出“内错角相等”的逆命题是 .
3.如图 ∠ A+∠B+ ∠C+ ∠D+ ∠E+ ∠F= .