2022年小升初数学典型应用题专项复习（全国通用） 专题06：植树问题（有答案，带解析）

这是一份2022年小升初数学典型应用题专项复习（全国通用） 专题06：植树问题（有答案，带解析），共8页。试卷主要包含了单选题，填空题，应用题等内容，欢迎下载使用。
一、单选题：
1.小区花园是一个长60米，宽40米的长方形，现在要在花园的四周栽树，四个角都要栽，每相邻两棵间隔5米。一共要栽( )棵。
A. 20 B. 36 C. 40 D. 44
2.6个小朋友排成一排，每相邻两个小朋友之间的距离是2米，则小朋友一共排了( )米。
A. 12 B. 10 C. 8 D. 14
3.在路边安装电线杆，每两根电线杆之间相隔8米，从第一根到最后一根电线一共长96米，一共安装了( )根电线杆．
A. 11根 B. 12根 C. 13根
4.一条30米长的直道一边，每隔2米放了一盆花，一共要放14盆花．正确的放法是（ ）
A. 两端都放 B. 只放一端 C. 两端都不放
5.将一根20米的铁丝剪成4米长的小段，需要剪（ ）次．
A. 4 B. 5 C. 6
二、填空题：
6.一个人从一楼走到三楼要走26个台阶，那么他从二楼走到七楼要走________个台阶。
7.在一条马路的两边挂彩灯，每两盏彩灯之间都相距4分米，两端都挂彩灯共挂1002盏，这条马路长________
8.公路的一侧有一排电线杆，每相邻两根之间的距离都是45米．现在要改成每相邻两根都是60米，如果起点的一根不动，下一根不用动的电线杆距离起点这根有________米？如果这条公路全长5400米，电线杆的位置改动后，一共有________根可以不动？
9.看图回答
①公路每一边都种了350棵树．两边一共有________棵树。
②如果公路的两端都种了树，那么，这条公路全长是________米。
(提示：上面画出了公路两端都种树的示意图，可以想：3棵树之间有几段？4棵树之间有几段……)
三、应用题：
10.一条路长1000米，在这条路的一旁安路灯，村头村尾都不装，每隔20米安装一盏，一共需要多少盏路灯？
11.同学们在全长240米的小路一边栽树，每隔4米栽一棵（两端都栽），一共需要多少棵树苗？

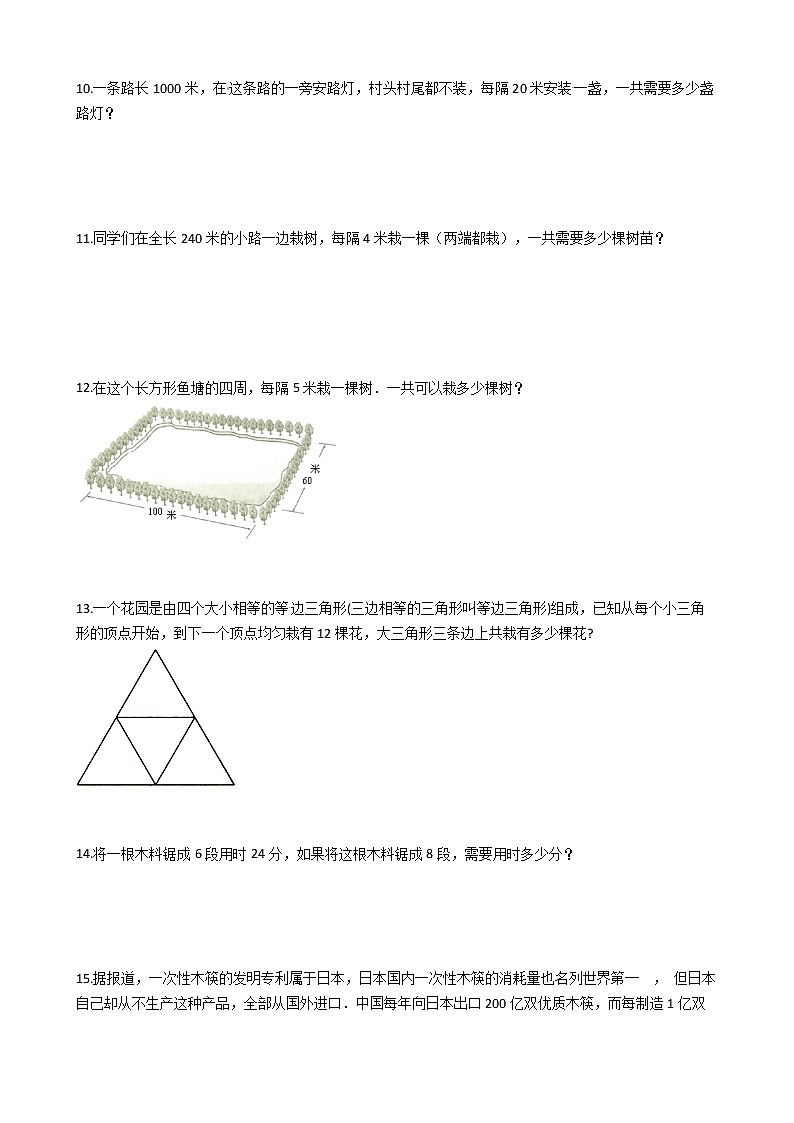
12.在这个长方形鱼塘的四周，每隔5米栽一棵树．一共可以栽多少棵树？
13.一个花园是由四个大小相等的等边三角形(三边相等的三角形叫等边三角形)组成，已知从每个小三角形的顶点开始，到下一个顶点均匀栽有12棵花，大三角形三条边上共栽有多少棵花?
14.将一根木料锯成6段用时24分，如果将这根木料锯成8段，需要用时多少分？
15.据报道，一次性木筷的发明专利属于日本，日本国内一次性木筷的消耗量也名列世界第一 ， 但日本自己却从不生产这种产品，全部从国外进口．中国每年向日本出口200亿双优质木筷，而每制造1亿双木筷就要用去0.2万立方米的木材，而每立方米木材大约相当于4棵大树．请问中国每年向日本出口200亿双木筷，需要砍去多少棵大树？
看到本题的计算结果，你有什么想法？请简要谈一谈．
16.下图是6个大小相同的铁环连成的链子．每个铁环长10厘米，铁环粗2厘米．这条链子全长多少厘米？如果同样的一条铁链子长154厘米，那么这条铁链子是由多少个铁环连成的？
17.圆形滑冰场的一周全长是150米，如果沿着这一圈每隔15米安装一盏灯，一共需要几盏灯？

18.数彩灯
新春佳节到了，长800米的大桥两侧挂起了彩灯.小红从起点数到终点，知道大桥两侧一共挂了202盏，而且她发现相邻两盏灯之间的距离都相等，你能帮小红算一算相邻两盏灯之间的距离吗？
答案解析部分
一、单选题
1.【答案】 C
【考点】植树问题
【解析】【解答】解：(60+40)×2÷5
=200÷5
=40(棵)
故答案为：C
【分析】由于是封闭的图形，且长和宽的长度都是5的倍数，那么可以直接用长方形的周长除以每相邻两棵间隔的长度求出一共要栽的棵数即可.
2.【答案】 B
【考点】植树问题
【解析】【解答】解：(6-1)×2
=5×2
=10(米)
故答案为：B
【分析】6个小朋友之间一共有5个间隔，因此用间隔数乘每两个小朋友之间的距离即可求出一共排了多少米.
3.【答案】 C
【考点】植树问题
【解析】【解答】96÷8+1
=12+1
=13(根)
故答案为：C
【分析】此题属于植树问题中的两端都植树问题，电线杆的根数要比间隔数多1，因此用96除以8求出间隔数，再加上1就是电线杆的根数.
4.【答案】C
【考点】植树问题
【解析】【解答】解：
30÷2=15（个）；
盆数比间隔数少15﹣14=1（个）；
只有两端不放时，盆数比间隔数少1．
故答案选：C．
【分析】根据题意，30÷2=15个间隔，而一共要放14盆花，盆数比间隔数少15﹣14=1个，然后再进一步解答即可．
5.【答案】A
【考点】植树问题
【解析】【解答】解：段数：20÷4=5（段）
剪了：5﹣1=4（次）
答：需要剪4次．
故答：A．
【分析】由题意，用20除以4即是段数：20÷4=5（段），再根据“剪的次数=段数﹣1”解答即可．
二、填空题
6.【答案】 65
【考点】植树问题
【解析】【解答】解：从一楼到三楼走了2层，一层台阶为：26÷2=13（个），从二楼走到七楼要走5层，5×13=65（个）.
故答案为：65.
【分析】首先求出一层有多少个台阶，再求出从二楼走到七楼要走5层，用层数乘一层台阶个数即可解答.
7.【答案】 200米
【考点】植树问题
【解析】【解答】1002÷2=501（盏）
4分米=0.4米
(501-1)×0.4
=500×0.4
=200（米）
故答案为：200米.
【分析】根据题意，用两边的彩灯总数÷2=道路一边的彩灯数量，然后用(彩灯数量-1)×每两盏彩灯之间的距离=马路的长度，据此解答.
8.【答案】 180；31
【考点】最小公倍数的应用，植树问题
【解析】【解答】45和60的最小公倍数是：5×3×3×2×2=180；
5400÷180+1
=30+1
=31（根）
故答案为：180；31.
【分析】根据题意，先求出45和60的最小公倍数，方法是：先用这几个数（或其中的部分数）的公因数去除，一直除到互质（或两两互质）为止，然后把所有的除数和商连乘求积，这个积就是这几个数的最小公倍数，然后用全长÷间隔+1=不移动的总根数，据此解答.
9.【答案】 700；1745
【考点】植树问题
【解析】【解答】①350×2=700(棵)
②(350-1)×5
=349×5
=1745(米)
故答案为：700；1745
【分析】①用每边种树的棵数乘2即可求出一共种树的棵数；②3棵数之间有2段，4棵数之间有3段，也就是段数比棵数少1，350棵树共有(350-1)段，用段数乘每段的长度即可求出路的长度.
三、应用题
10.【答案】 解：1000÷20－1=50－1=49(盏)答：一共需要49盏路灯.
【考点】植树问题
【解析】【分析】由于两端都不装，所以路灯盏数=间隔数-1，用路的长度除以间隔的长度即可求出间隔数，再减去1就是路灯的盏数.
11.【答案】 解：240÷4+1=60+1=61(棵)答：一共需要61棵树苗.
【考点】植树问题
【解析】【分析】由于是两端都栽，那么植树棵数=间隔数+1，用小路的长度除以间隔的米数即可求出间隔数，再加上1就是树苗棵数.
12.【答案】 64棵

【考点】植树问题
【解析】【解答】(100＋60)×2÷5
=160×2÷5
=320÷5
＝64（棵）
答：一共可以栽64棵树.
【分析】根据封闭图形的植树问题的解题方法：株数＝全长÷株距，据此先用长方形的周长公式求出长方形的周长，然后除以株距即可解答.
13.【答案】12－2=10(棵)，10×6=60(棵)，60+6=66(棵)

【考点】植树问题
【解析】【分析】根据题意可知，先求出每条边上除去两个顶点栽了几棵花，然后求出6条边除去顶点栽的棵数，最后加上6个顶点的棵数，据此解答.
14.【答案】24÷(6－1)×(8－1)=33.6(分)

【考点】植树问题
【解析】【解答】24÷(6－1)×(8－1)
=24÷5×7
=4.8×7
=33.6（分）
答：需要用时33.6分.
【分析】根据题意可知，将一根木料锯成6段，需要锯（6-1）次，用锯的总时间÷锯的次数=每次需要的时间，同样的道理，锯成8段，需要锯（8-1）次，然后用每次需要的时间×锯的次数=需要的总时间，据此解答.
15.【答案】 解：200×0.2×4=160(万棵)
【考点】植树问题
【解析】【分析】：我们要植树造林，减少滥伐滥砍，保护环境，爱护我们的家园。
16.【答案】50厘米；19个.

【考点】植树问题
【解析】【解答】
解：10×6－2×(6－1)
＝60－2×5
＝60－10
＝50(厘米)
答：这条链子全长50厘米.
(154－2)÷(10－2)
＝152÷8
＝19(个)
或设x个铁环
10x-2(x-1)=154
10x－2x＋2＝154
8x＝152
x=19
答：这条铁链子是由19个铁环连成的.
【分析】解答本题的关键是明确如果在非封闭线路的两端都要植树，那么：段数＝株数－1.
17.【答案】解：根据题意可得：
150÷15=10（盏）．
答：一共需要装10盏灯
【考点】植树问题
【解析】【分析】根据题意，在圆形上植树，植树的棵树与间隔数相等，直接用150除以15即可．
18.【答案】8米

【考点】植树问题
【解析】【解答】800÷(202÷2-1)
=800÷(101-1)
=800÷100
=8（米）
答：相邻两盏灯之间的距离是8米.
【分析】根据植树问题的解答方法，先求出大桥每边各挂多少盏灯，然后求出101盏彩灯把800米长的大桥分成多少段，然后用总长度÷段数=相邻两盏彩灯之间的距离，据此解答.