2022届广东省深圳市高三下学期第二次调研考试（二模）（4月）数学试题word版含答案

试卷类型：A

2022年深圳市高三年级第二次调研考试

2022.4

数学

本试卷共6页，22小题，满分150分．考试用时120分钟。

注意事项：

1．答卷前，考生务必用黑色字迹的签字笔在答题卡指定位置填写自己的学校、姓名和考生号，并将条形码正向准确粘贴在答题卡的贴条形码区，请保持条形码整洁、不污损.

2．选择题每小题选出答案后，用2B铅笔把答案涂在答题卷相应的位置上．

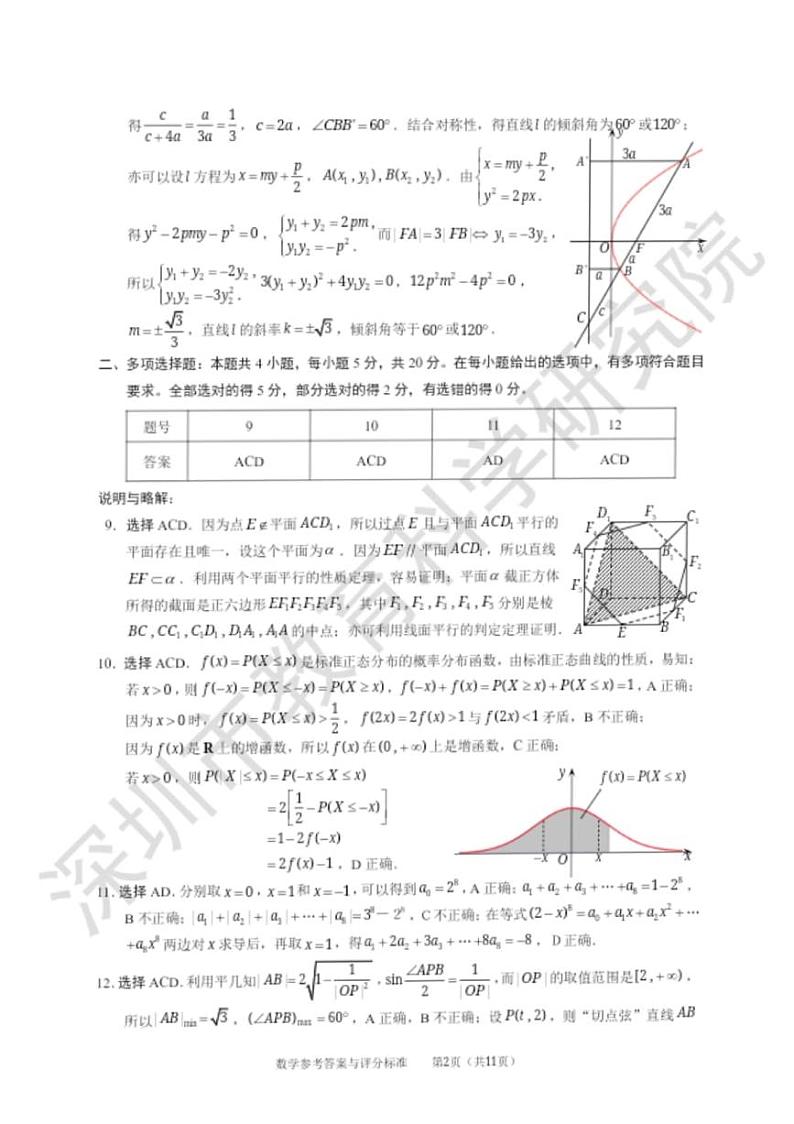
3．非选择题必须用0.5毫米黑色字迹的签字笔作答，答案必须写在答题卡各题目指定区域内；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.

4．考生必须保持答题卡的整洁，考试结束后，将答题卡交回．

一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A＝｛x|x＜1｝，B＝｛x|x(x-2)＜0｝，则A∪B＝

A.(0,1)      B.(1,2)      C.(- ∞,2)      D.(0,+ ∞)

2．已知复数z满足zi＝3＋4i，其中i为虚数单位，则｜z｜＝

A.3           B.4               C.5              D.6

3．已知点A（0,1），B（2,3），向量＝(-3,1)，则向量＝

A.(1,-2)      B.(-1,2)   C.(1,-3)       D.(-1,3)

4．深圳是一座志愿者之城、爱心之城．深圳市卫健委

为了解防疫期间志愿者的服务时长（单位：小时），对参加过防疫的志愿者随机抽样调查，将样本中个体的服务时长进行整理，得到如图所示的频率分布直方图．据此估计，7.2万名参加过防疫的志愿者中服务时长超过32小时的约有

A．3.3万人

B．3.4万人

C．3.8万人

D．3.9万人

5．已知一个球的表面积在数值上是它的体积的倍，则这个球的半径是

A.2             B.               C.3              D.

6．若x＝是函数f（x）＝cosωx（ω≠0）图象的对称轴，则f（x）的最小正周期的最大值是

A.π                B.2π              C.              D.

7．已知a＞0，若过点（a，b）可以作曲线y＝x3的三条切线，则

A.b<0          B.0<b<a3               C.b>a3           D.b(b-a3)=0

8．过抛物线y2＝2px（p＞0）的焦点F作直线l，交抛物线于A，B两点，若|FA|＝3|FB|，

则直线l的倾斜角等于

A．30°或150°      B．45°或135°        C．60°或120°      D.  与p值有关

二、多项选择题：本题共4小题，每小题5分，共20分。在每小题给出的选项中，有多

项符合题目要求。全部选对的得5分，部分选对的得2分，有选错的得0分。

9．如图，在正方体ABCD-A1B1C1D1中，E为AB的中点，则下列条件中，能使直线EF∥平面ACD1的有

A.F为AA1的中点                  B.F为BB1的中点

C．F为CC1的中点               D．F为A1D1的中点

10．已知随机变量X服从正态分布N（0,1），密度函数f（x）＝P（X≤x），若x＞0，则

A.f(-x)=1-f(x)                                                             B.f(2x)=2f(x)

C．f（x）在（0，＋oo）上是增函数                    D.P(|X|≤x)=2f(x)-1

11．已知(2-x)8＝ao＋a1x＋a2x2＋···＋a8x8，则

A.ao=28                                                               B.a1+a2+··+a6=1

C..|a1|+|a2|+|a3|+…+|a8|=38                   D.a1+2a2+3a3+···+8a8= -8

12．P是直线y＝2上的一个动点，过点P作圆x2＋y2＝1的两条切线，A，B为切点，则

A．弦长|AB|的最小值为          B．存在点P，使得∠APB＝90°

C.直线AB经过一个定点                D.线段AB的中点在一个定圆上

三、填空题：本题共4小题，每小题5分，共20分。

13．已知tanα＝3，则cos2α＝          .

14．已知0＜x＜1，则的最小值是          .

15．已知函数f（x）＝1n（ex＋1）-kx是偶函数，则k＝          .

16．祖暅是我国南北朝时期伟大的科学家，他于5世纪末提出了“幂势既同，则积不容异”的体积计算原理，即“夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等”.现已知直线y＝±2与双曲线x2-y2＝1及其渐近线围成的平面图形G如图所示．若将图形G被直线y＝t（-2≤t≤2）所截得的两条线段绕y轴旋转一周，则形成的旋转面的面积S＝        ；若将图形G绕y轴旋转一周，则形成的旋转体的体积V＝          .

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

17．（10分）已知数列{an}的前n项和Sn＝2an-3．

（1）求数列{an}的通项公式；

（2）若，求满足条件的最大整数n.

·18．（12分）记ΔABC的内角A，B，C的对边分别为a，b，c，已知a＋c＝2bcosA．

（1）证明：B＝2A；

（2）当a＝4，b＝6时，求ΔABC的面积S．

19．（12分）如图，在四棱锥P-ABCD中，底面ABCD为正方形，侧面PAD是正三角

形，M是侧棱PD的中点，且AM⊥平面PCD．

（1）求证：平面PAD⊥平面ABCD；

（2）求AM与平面PBC所成角的正弦值．

20．（12分）2022年北京冬奥会后，由一名高山滑雪运动员甲组成的专业队，与两名高山滑雪爱好者乙、丙组成的业余队进行友谊比赛，约定赛制如下：业余队中的两名队员轮流与甲进行比赛，若甲连续赢两场则专业队获胜；若甲连续输两场则业余队获胜；若比赛三场还没有决出胜负，则视为平局，比赛结束.

已知各场比赛相互独立，每场比赛都分出胜负，且甲与乙比赛，乙赢的概率为，甲与丙比赛，丙赢的概率为P，其中.

（1）若第一场比赛，业余队可以安排乙与甲进行比赛，也可以安排丙与甲进行比赛。请分别计算两种安排下业余队获胜的概率；若以获胜概率大为最优决策，问：业余队第一场应该安排乙还是丙与甲进行比赛？

（2）为了激励专业队和业余队，赛事组织规定：比赛结束时，胜队获奖金3万元，负队获奖金1.5万元；若平局，两队各获奖金1.8万元．

在比赛前，已知业余队采用了（1）中的最优决策与甲进行比赛，设赛事组织预备支付的奖金金额共计X万元，求X的数学期望E（X）的取值范围.

21．（12分）已知椭圆E：＝1（a＞b＞0）经过点M(1，），且焦距|F1F2|＝2，

线段AB，CD分别是它的长轴和短轴.

（1）求椭圆E的方程；

（2）若N（s，t）是平面上的动点，从下面两个条件中选一个，证明：直线PQ经过定点．

①s=1,t≠ ±,直线NA，NB与椭圆E的另一交点分别为P，Q；

②t＝2，s∈R，直线NC，ND与椭圆E的另一交点分别为P，Q．

22．（12分）设函数f（x）＝xex-ax2-2ax＋2a2-a，其中a∈R．

（1）讨论f（x）的单调性；

（2）当f（x）存在小于零的极小值时，若x1，x2∈（0，），且f（sinx1）＜f（x1cosx2），

证明：x1＞x2·