沪科版八年级下册18.1 勾股定理习题ppt课件

这是一份沪科版八年级下册18.1 勾股定理习题ppt课件，共30页。PPT课件主要包含了答案呈现，习题链接等内容，欢迎下载使用。

下列各组线段中，不能够组成直角三角形的是(　　)A．6，8，10 B．3，4，5C．4，5，6 D．5，12，13
若△ABC的三边长a，b，c满足(a－b)(a2＋b2－c2)＝0，则△ABC是(　　)A．等腰三角形 B．直角三角形C．等边三角形 D．等腰三角形或直角三角形
【2021·扬州】如图，在4×4的正方形网格中有两个格点A、B，连接AB，在网格中再找一个格点C，使得△ABC是等腰直角三角形，满足条件的格点C的个数是(　　)A．2 B．3 C．4 D．5
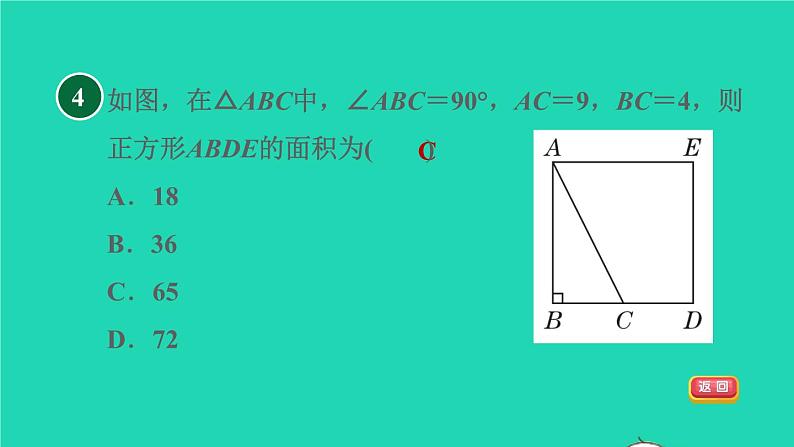
如图，在△ABC中，∠ABC＝90°，AC＝9，BC＝4，则正方形ABDE的面积为(　　)A．18 B．36 C．65 D．72
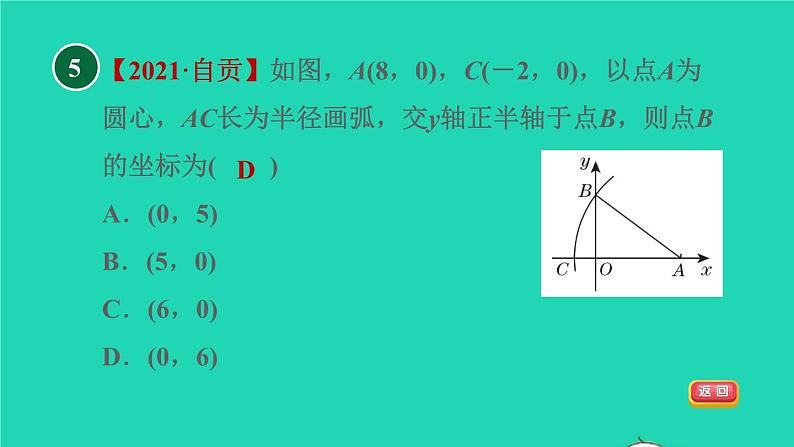
【2021·自贡】如图，A(8，0)，C(－2，0)，以点A为圆心，AC长为半径画弧，交y轴正半轴于点B，则点B的坐标为(　　)A．(0，5) B．(5，0)C．(6，0) D．(0，6)
如图，把长为8 cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3 cm至点D，则橡皮筋被拉长了(　　)A．2 cm B．3 cm C．4 cm D．5 cm
如图，在长方形ABCD中，AB＝3 cm，AD＝9 cm，将此长方形折叠，使点D与点B重合，折痕为EF，则△ABE的面积为(　　)A．3 cm2 B．4 cm2 C．6 cm2 D．12 cm2
【2021·烟台】由12个有公共顶点O的直角三角形拼成的图形如图所示，∠AOB＝∠BOC＝…＝∠LOM＝30°，若OA＝16，则OG的长为(　　)
请你任意写出两组勾股数：______________________________________．
3，4，5；6，8，10(答案不唯一)
在△ABC中，∠C＝90°，AB＝5，则AB2＋AC2＋BC2＝________．
【中考·辽阳】如图，在Rt△ABC中，∠ACB＝90°，AC＝2BC，分别以点A和B为圆心，以大于12AB的长为半径作弧，两弧相交于点M和N，作直线MN，交AC于点E，连接BE，若CE＝3，则BE的长为________．
如图，在离水面高度为8 m的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为17 m，此人以每秒1 m的速度收绳，7 s后船移动到点D的位置，则船向岸边移动了________m(假设绳子是直的)．
如图，圆柱底面的周长为6 dm，圆柱高为4 dm，在圆柱的侧面上，过点A和点C嵌有一圈金属丝，则这圈金属丝的长度最小为________．
(7分)如图，在四边形ABCD中，AB＝BC＝2，CD＝3，DA＝1，且∠B＝90°，求∠DAB的度数．
解：如图，连接AC.∵∠B＝90°，AB＝BC＝2，∴AC2＝AB2＋BC2＝8，∠BAC＝45°.又∵CD＝3，DA＝1，∴AC2＋DA2＝8＋1＝9，CD2＝9.∴AC2＋DA2＝CD2.∴△ACD是直角三角形，且∠CAD＝90°.∴∠DAB＝45°＋90°＝135°.
(10分)如图，已知等腰三角形ABC的底边BC的长为10，D是AC上的一点，其中BD＝8，CD＝6．(1)求证：BD⊥AC；
证明：∵BC＝10，BD＝8，CD＝6，∴BD2＋CD2＝82＋62＝102＝BC2.∴△BDC是直角三角形，且∠BDC＝90°，即BD⊥AC.
(7分)如图，小明想知道学校旗杆的高，他发现旗杆顶端的绳子垂到地面还多1米，当他把绳子的下端拉开与旗杆底部相距5米时，发现绳子下端刚好接触地面，求旗杆的高度．
解：设旗杆的高度为x米，由题意知绳子的长度为(x＋1)米．由勾股定理列方程x2＋52＝(x＋1)2，解得x＝12.答：旗杆的高度为12米．
(10分)一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的证明方法．如图①，火柴盒的一个侧面ABCD倒下到AEFG的位置，连接CF，AB＝a，BC＝b，AC＝c．(1)请你结合图②用文字和符号语言分别叙述勾股定理；
解：直角三角形两直角边的平方和等于斜边的平方．在Rt△ABC中，∠C＝90°，BC＝a，AC＝b，AB＝c，则有a2＋b2＝c2.
(2)请利用直角梯形BCFG的面积证明勾股定理：a2＋b2＝c2．
(10分)定义：如图，点M，N把线段AB分割成AM，MN，NB，若以AM，MN，NB为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．(1)若AM＝1.5，MN＝2.5，BN＝2，则点M，N是线段AB的勾股分割点吗？请说明理由．
解：点M，N是线段AB的勾股分割点．理由：∵AM2＋BN2＝1.52＋22＝6.25，MN2＝2.52＝6.25，∴AM2＋BN2＝MN2.∴以AM，MN，NB为边的三角形是一个直角三角形．∴点M，N是线段AB的勾股分割点．
(2)已知点M，N是线段AB的勾股分割点，且AM为直角边，若AB＝24，AM＝6，求BN的长．