初中沪科版第19章 四边形综合与测试习题ppt课件

这是一份初中沪科版第19章 四边形综合与测试习题ppt课件，共36页。PPT课件主要包含了答案呈现，习题链接，AD＝AB等内容，欢迎下载使用。
在平行四边形、矩形、菱形、正方形中，既是轴对称图形又是中心对称图形的有(　　)A．1个 B．2个 C．3个 D．4个
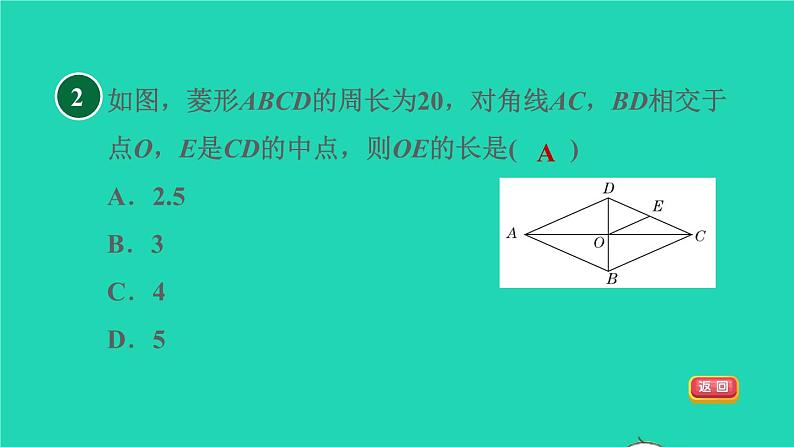
如图，菱形ABCD的周长为20，对角线AC，BD相交于点O，E是CD的中点，则OE的长是(　　)A．2.5 B．3 C．4 D．5
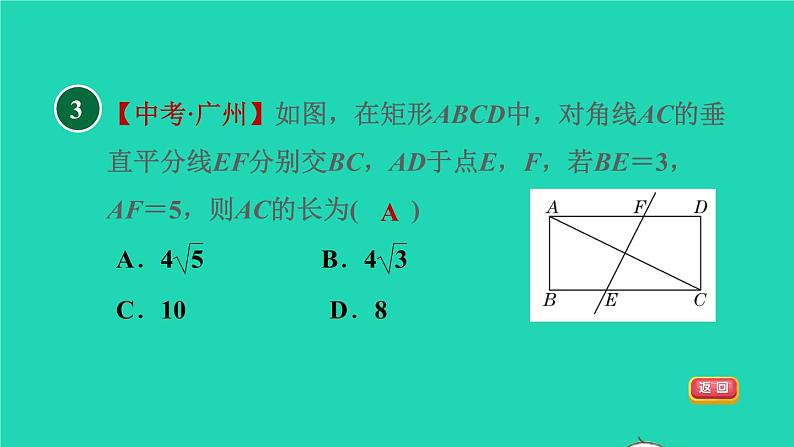
【中考·广州】如图，在矩形ABCD中，对角线AC的垂直平分线EF分别交BC，AD于点E，F，若BE＝3，AF＝5，则AC的长为(　　)
【中考·黄石】如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB边的中点是坐标原点O，将正方形绕点C按逆时针方向旋转90°后，点B的对应点B′的坐标是(　　)A．(－1，2) B．(1，4)C．(3，2) D．(－1，0)
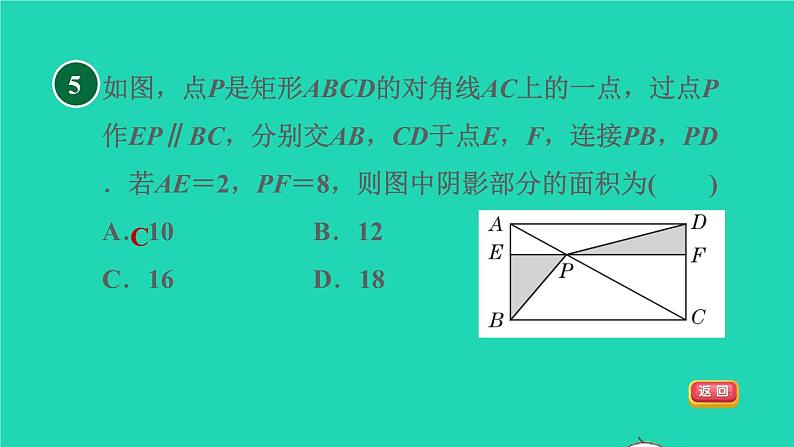
如图，点P是矩形ABCD的对角线AC上的一点，过点P作EP∥BC，分别交AB，CD于点E，F，连接PB，PD．若AE＝2，PF＝8，则图中阴影部分的面积为(　　)A．10 B．12 C．16 D．18
如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是(　　)A．AB∥DCB．AC＝BDC．AC⊥BDD．AB＝DC
【中考·天津】如图，四边形ABCD为菱形，A，B两点的坐标分别是(2，0)，(0，1)，点C，D在坐标轴上，则菱形ABCD的周长等于(　　)
【中考·北京】把图①中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图②、图③所示的正方形，则图①中菱形的面积为________．
如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E，若∠CBF＝20°，则∠AED等于__________°．
如图，在矩形ABCD中，AE＝AF，过点E作EH⊥EF交DC于点H，过点F作FG⊥EF交BC于点G，当AD，AB满足__________时，四边形EFGH为矩形．
如图，两个完全相同的三角板ABC和DEF在直线l上滑动．要使四边形CBFE为菱形，还需添加的一个条件是___________________ (写出一个即可)．
CB＝BF(答案不唯一)
如图，在菱形ABCD中，∠A＝110°，E，F分别是AB和BC的中点，EP⊥CD于点P，则∠FPC等于______．
【中考·安顺】如图，在Rt△ABC中，∠BAC＝90°，且BA＝3，AC＝4，点D是斜边BC上的一个动点，过点D分别作DM⊥AB于点M，DN⊥AC于点N，连接MN，则线段MN的最小值为________．
(10分)【2021·恩施州】如图，矩形ABCD的对角线AC，BD交于点O，且DE∥AC，AE∥BD，连接OE．求证：OE⊥AD．
证明：∵DE∥AC，AE∥BD，∴四边形AODE为平行四边形．∵四边形ABCD为矩形，∴OA＝OD.∴平行四边形AODE为菱形．∴OE⊥AD.
(10分)【2021·菏泽】如图，在菱形ABCD中，点M，N分别在AB，CB上，且∠ADM＝∠CDN．求证：BM＝BN．
(10分)【中考·青岛】如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别在BD和DB的延长线上，且DE＝BF，连接AE，CF．(1)求证：△ADE≌△CBF．
(2)连接AF，CE．当BD平分∠ABC时，四边形AFCE是什么特殊四边形？请说明理由．
解：如图，当BD平分∠ABC时，四边形AFCE是菱形．理由：∵BD平分∠ABC，∴∠ABD＝∠CBD.∵∠ADB＝∠CBD，∴∠ABD＝∠ADB. ∴AB＝AD.∴平行四边形ABCD是菱形．∴AC⊥BD，即AC⊥EF.∵四边形ABCD是平行四边形，
∴OA＝OC，OB＝OD.∵DE＝BF，∴OE＝OF.∴四边形AFCE是平行四边形．又∵AC⊥EF，∴四边形AFCE是菱形．
(14分)【中考·天水】如图①，对角线互相垂直的四边形叫做垂美四边形．(1)概念理解：如图②，在四边形ABCD中，AB＝AD，CB＝CD，问四边形ABCD是垂美四边形吗？请说明理由．
解：四边形ABCD是垂美四边形．理由：连接BD，AC.∵AB＝AD，∴点A在线段BD的垂直平分线上．∵CB＝CD，∴点C在线段BD的垂直平分线上．∴直线AC是线段BD的垂直平分线．∴AC⊥BD，即四边形ABCD是垂美四边形．
(2)性质探究：如图①，四边形ABCD的对角线AC，BD交于点O，AC⊥BD．求证：AB2＋CD2＝AD2＋BC2．
证明：∵AC⊥BD，∴∠AOD＝∠AOB＝∠BOC＝∠COD＝90°.由勾股定理，得AB2＋CD2＝AO2＋BO2＋CO2＋DO2，AD2＋BC2＝AO2＋DO2＋BO2＋CO2，∴AB2＋CD2＝AD2＋BC2.
(3)解决问题：如图③，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE．已知AC＝4，AB＝5，求GE的长．
∴∠ABG＝∠AEC.又∵∠AEC＋∠AME＝90°，∠AME＝∠BMC，∴∠ABG＋∠BMC＝90°.∴CE⊥BG.∴四边形CGEB是垂美四边形．由(2)得CG2＋BE2＝CB2＋GE2.